Laboratory Synthesis of the Mineral Hedenbergite
- Page ID
- 49940
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Equations and Mass Relationships in Geology
Mineralogists often synthesize minerals to verify the composition of naturally occurring minerals by preparing them synthetically. Sometimes minerals are first synthesized, and only later, when their properties are known, are they found in nature. Synthesizing related minerals in the laboratory can also help understand how the formations came to be in nature. For example, the mineral Hedenbergite is rarely found in nature, but it has been synthesized [1][2] in the laboratory.


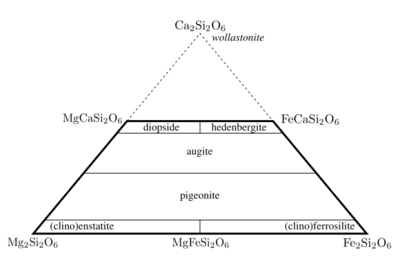
The pyroxene family to which it belongs the variation in composition as shown in the composition diagram below. Hedenbergite has one Fe2+ ion and one Ca2+ ion associated with a chain of tetrahedral silicate groups [~O-Si(O2)-O-Si(O2)-O~]. Other pyroxenes include Fe2Si2O6 and MgCaSi2O6, but Wollastonite (Ca2Si2O6) has a different structure and is not classified as a pyroxene. Some pyroxenes have Al3+ in place of the Si in the tetrahedral chains. This variation is typical of minerals with chains of silicate tetrahedra [3], and results in mineral samples from adjacent locations that are slightly different in composition and appearance. Mixtures of the various minerals are common. A synthesis therefore has to combine the elements in the proper proportions to prepare Hedenbergite and not another pyroxene.
The chemical equation
\[\ce{CaO + FeO + 2Si O2 → CaFeSi2O6} \label{1}\]
tells us that we might be able to make hedenbergite by grinding a mixture of CaO (lime), FeO, and SiO2 (sand) together in a mortar or mill. The mixture has to be heated to 1000oC for a week or so at 1 Atm pressure to complete the reaction. In reality, CaCO3 (limestone) is used in place of CaO (which is unstable with respect to reaction with humid air to form Ca(OH)2, H2SiO2 is used in place of SiO2and Fe2O3 is used in place of the unstable FeO (which oxidizes slowly in air to Fe2O3). Nonetheless, the simplified equation above can be used[4] [5].
We can use the balanced chemical equation \(\ref{1}\) to calculate the optimal ratio of reactants. It not only tells how many atoms, molecules, or "formula units" [6] of each kind are involved in a reaction, it also indicates the amount of each substance that is involved. Equation (1) says that 2 SiO2 formula units can react with 1 CaO formula units and 1 FeO formula units to give 1 CaFeSi2O6 formula unit. It also says that 2 mol SiO2 would react with 1 mol CaO and 1 mol FeO, yielding 1 mol CaFeSi2O6.
The balanced equation does more than this, though. It also tells us that 2 × 2 = 4 mol SiO2 will react with 2 × 1 = 2 mol CaO, and that ½ × 2 = 1 mol SiO2 requires only ½ × 1 = 0.5 mol CaO. In other words, the equation indicates that exactly 1 CaO must react for every 2 mol SiO2 consumed. For the purpose of calculating how much CaO is required to react with a certain amount of SiO2 therefore, the significant information contained in Equation (1) is the ratio
\( \ce{ \dfrac{1 ~mol~ CaO}{2~ mol ~SiO_{2}}}\)
We'll call such a ratio derived from a balanced chemical equation a stoichiometric ratio and give it the symbol S. Thus, for Equation \(\ref{1}\),
\[ \ce{ S \dfrac{CaO}{SiO_{2}} = \dfrac{1 ~mol~ CaO}{2 ~mol~ SiO_{2}} \quad (2) }\]
The word stoichiometric comes from the Greek words stoicheion, “element,“ and metron, “measure.“ Hence the stoichiometric ratio measures one element (or compound) against another.
EXAMPLE \(\PageIndex{1}\): Stoichiometric Ratios
Derive other possible stoichiometric ratios from Equation \(\ref{1}\)
Solution: Any ratio of amounts of substance given by coefficients in the equation may be used:
\( \ce{S \dfrac{SiO_{2}}{CaO} = \dfrac{2~mol~SiO_{2}}{1~mol~CaO} \quad S \dfrac{SiO_{2}}{FeO} = \dfrac{2~mol~SiO_{3}}{1~mol~FeO} }\)
\( \ce{S \dfrac{SiO_{2}}{CaFeSi_{2}O_{6}} = \dfrac{2~mol~SiO_{2}}{1~mol~CaFeSi_{2}O{6}} \qquad S \dfrac{CaFeSi_{2}O_{6}}{FeO} = \dfrac{1~mol~CaFeSi_{2}O_{6}}{1~mol~FeO}} \)
\(\text{S}\left( \dfrac{\text{CaO}}{\text{FeO}} \right)=\dfrac{\text{1 mol CaO}}{\text{1 mol FeO}}~ ~ ~ ~ ~\text{S}\left( \dfrac{\text{FeO}}{\text{SiO}_{\text{2}}} \right)=\dfrac{\text{1 mol FeO}}{\text{2 mol SiO}_{\text{2}}}\)
When any chemical reaction occurs, the amounts of substances consumed or produced are related by the appropriate stoichiometric ratios. Using Equation (1) as an example, this means that the ratio of the amount of SiO2 consumed to the amount of CaO consumed must be the stoichiometric ratio S(SiO2/CaO):
\(\dfrac{n_{\text{SiO}_{2}}\text{ consumed}}{n_{\text{CaO}}\text{ consumed}}~ ~=~ ~\text{S}\left( \dfrac{\text{SiO}_{2}}{\text{CaO}} \right)=\dfrac{\text{2 mol SiO}_{2}}{\text{1 mol CaO}}\)
Similarly, the ratio of the amount of CaFeSi2O6 produced to the amount of SiO2 consumed must be
S(K2S/SiO2):
\(\dfrac{n_{\text{CaFeSi}_{2}\text{0}_{\text{6}}\text{ produced}}}{n_{\text{SiO}_{\text{2}}\text{ consumed}}}=\text{S}\left( \dfrac{\text{CaFeSi}_{2}\text{0}_{\text{6}}}{\text{SiO}_{2}} \right)=\dfrac{\text{1 mol CaFeSi}_{2}\text{0}_{\text{6}}}{\text{2 mol SiO}_{2}}\)
In general we can say that
\( \text{Stoichiometric ratio }\left( \dfrac{\text{X}}{\text{Y}} \right)=\dfrac{\text{amount of X consumed or produced}}{\text{amount of Y consumed or produced}}~ ~ ~ ~ ~(3a) \)
or, in symbols,
\(\text{S}\left( \dfrac{\text{X}}{\text{Y}} \right)=\dfrac{n_{\text{X consumed or produced}}}{n_{\text{Y consumed or produced}}}~ ~ ~ ~ ~ ~ (3b) \)
Note
Note that in the word Equation (3a) and the symbolic Equation (3b), X and Y may represent any reactant or any product in the balanced chemical equation from which the stoichiometric ratio was derived. No matter how much of each reactant we have, the amounts of reactants consumed and the amounts of products produced will be in appropriate stoichiometric ratios.
EXAMPLE \(\PageIndex{2}\): Amount Produced
Find the amount of CaFeSi2O6 that will be produced when 0.00806 mol SiO2 is consumed according to Equation \(\ref{1}\).
Solution
The amount of CaFeSi2O6 produced must be in the stoichiometric ratio S(CaFeSi2O6/SiO2) to the amount of potassium nitrate consumed:
\( \text{S}\left( \dfrac{\text{CaFeSi}_{2}\text{0}_{\text{6}}}{\text{SiO}_{\text{2}}} \right)=\dfrac{n_{\text{CaFeSi}_{2}\text{0}_{\text{6}}}\text{ produced}}{n_{\text{SiO}_{\text{2}}}\text{ consumed}} \)
Multiplying both sides by nKNO3 consumed, by we have
\( n_{\text{SiO}_{\text{2}}\text{ consumed}}\times \text{S}\left( \dfrac{\text{CaFeSi}_{2}\text{0}_{\text{6}}}{\text{SiO}_{\text{2}}} \right)~=~n_{\text{CaFeSi}_{2}\text{0}_{\text{6}}}\text{ produced} \)
\(~=~\text{0}\text{.00806 mol SiO}_{\text{2}}\times \dfrac{\text{1 mol CaFeSi}_{2}\text{0}_{\text{6}}}{\text{2 mol SiO}_{\text{2}}}=\text{0.00403 mol}\text{ CaFeSi}_{2}\text{0}_{\text{6}} \)
This is a typical illustration of the use of a stoichiometric ratio as a conversion factor. Example 2 is analogous to Examples 1 and 2 from Conversion Factors and Functions, where density was employed as a conversion factor between mass and volume. Example 2 is also analogous to Examples 2.4 and 2.6, in which the Avogadro constant and molar mass were used as conversion factors. As in these previous cases, there is no need to memorize or do algebraic manipulations with Equation (3) when using the stoichiometric ratio. Simply remember that the coefficients in a balanced chemical equation give stoichiometric ratios, and that the proper choice results in cancellation of units. In road-map form

or symbolically.
\(n_{\text{X consumed or produced}}\text{ }\overset{S\text{(X/Y)}}{\longleftrightarrow}\text{ }n_{\text{Y consumed or produced}}\)
When using stoichiometric ratios, be sure you always indicate moles of what. You can only cancel moles of the same substance. In other words, 1 mol KNO3 cancels 1 mol KNO3 but does not cancel 1 mol CO2.
The next example shows that stoichiometric ratios are also useful in problems involving the mass of a reactant or product.
EXAMPLE \(\PageIndex{3}\): Produc
Calculate the masses of CaO and FeO that will react with 0.484 g of SiO2 according to equation \(\ref{1}\), and the masses of all products that will form. This will solve the problem of which recipe for hedenbergite is optimal[7].
Solution: The problem asks that we calculate the masses of reactants and products. As we learned in Example 2 of The Molar Mass, the molar mass can be used to convert from the amount of any substance to its mass. So we can calculate the amount of SiO2 available:
\( n_{\text{SiO}_{2}} = \dfrac{m_{\text{SiO}_{2}}}{M_{\text{SiO}_{2}}}=\dfrac{0.484g}{\dfrac{60.1g}{mol~\text{SiO}_{2}}}=0.00806~mol~\text{SiO}_{2} \)
Now we need to calculate the amounts of reactants and products from the amount of SiO2 consumed. This is similar to Example 2. It requires stoichiometric ratios like
\(\text{S}\left( \dfrac{\text{CaO}}{\text{SiO}_{\text{2}}} \right)=\dfrac{\text{1 mol CaO}}{\text{2 mol SiO}_{\text{2}}} \)
The amount of CaO consumed is then
\(n_{\text{CaO}}\text{ consumed} ~=~ n_{\text{SiO}_{2}}\text{ consumed}~ ~\times~\text{ conversion factor} \)
\(~=~ \text{0.00806 mol SiO}_{2}\times \dfrac{\text{1 mol CaO}}{\text{2 mol SiO}_{2}}=\text{0.00403 mol CaO}\)
The mass of CaO is
\(\text{m}_{\text{CaO}}=\text{0.00403 mol CaO}\times \dfrac{\text{56}\text{.1 g CaO}}{\text{1 mol CaO}}~=~\text{0.226 g CaO} \)
With practice this kind of problem can be solved in one step by concentrating on the units. The appropriate stoichiometric ratio will convert moles of O2 to moles of SO2 and the molar mass will convert moles of SO2 to grams of SO2. A schematic road map for the one-step calculation can be written as
\(n_{\text{SiO}_{\text{2}}}\) \( ~\xrightarrow{S\text{(CaO}\text{/SiO}_{\text{2}}\text{)}} \) \( ~ n_{\text{CaO}} ~ \xrightarrow{M_{\text{CaO}}} ~ m_{\text{CaO}} \)
Thus
\( \text{m}_C ~=~ \text{0.00806 mol SiO}_{\text{2}} ~ \times ~\dfrac{\text{1 mol CaO}}{\text{2 mol SiO}_{\text{2}}} ~\times ~\dfrac{\text{56.1 g}}{\text{1 mol CaO}}=\text{0.226 g} \)
These calculations can be organized as a table, with entries below the respective reactants and products in the chemical equation.
- + 2 SiO2
| CaO | + FeO | + 2 SiO2 → | CaFeSi2O6 | |
|---|---|---|---|---|
| m (g) | 0.226 | 0.289 | 0.484 | 0.999 |
| M (g/mol) | 56.1 | 71.8 | 60.1 | 248.1 |
| n (mol) | 0.00403 | 0.00403 | 0.00806 | 0.00403 |
The masses of products are calculated in a similar way, for example:
\(\text{m}_{\text{CaFeSi}_{2}\text{0}_{\text{6}}}~=~ \text{0.00806 mol SiO}_{\text{2}} ~ \times ~\dfrac{\text{1 mol CaFeSi}_{2}\text{0}_{\text{6}}}{\text{2 mol SiO}_{\text{2}}} ~\times ~\dfrac{\text{248.1 g}}{\text{CaFeSi}_{2}\text{0}_{\text{6}}}=\text{0.999 g}\)
EXAMPLE 4:
What mass of Fe2O3 would be consumed when 0.626 g of H2SiO3 reacts (with stoichiometric CaCO3 present) to produce CaFeSi2O6, CO2, and H2O?
Solution: First, write a balanced equation
\[\ce{ 2CaCO3 + Fe2O3 + 2H2SiO3 → CaFeSi2O6 + 2CO2 + 2.5O2}\]
The problem gives the mass of metasilicic acid, H2SiO3 and asks for the mass of Fe2O3 required to combine with it. Thinking the problem through before trying to solve it, we realize that the molar mass of metasilicic acid could be used to calculate the amount of metasilicic acid consumed. Then we need a stoichiometric ratio to get the amount of Fe2O3 consumed. Finally, the molar mass of Fe2O3 permits calculation of the mass of Fe2O3. Symbolically
\(m_{\text{H}_{\text{2}}\text{SiO}_{\text{3}}}\text{ }\xrightarrow{M_{\text{H}_{\text{2}}\text{SiO}_{\text{3}}}}~~n_{\text{H}_{\text{2}}\text{SiO}_{\text{3}}}~~\xrightarrow{S\text{(Fe}_{\text{2}}\text{O}_{3}\text{/H}_{\text{2}}\text{SiO}_{\text{3}}\text{)}}\text{ }n_{\text{Fe}_{2}\text{O}_{\text{3}}}\xrightarrow{M_{\text{Fe}_{2}\text{O}_{\text{3}}}}\text{ }m_{\text{Fe}_{2}\text{O}_{\text{3}}} \)
\( m_{\text{Fe}_{2}\text{O}_{\text{3}}}=\text{0.626 g }~~\times ~~\dfrac{\text{1 mol H}_{\text{2}}\text{SiO}_{\text{3}}}{\text{78.1 g}}~~\times ~~\dfrac{\text{1 mol Fe}_{\text{2}}\text{O}_{3}}{\text{2 mol H}_{\text{2}}\text{SiO}_{\text{3}}}~~\times~~\dfrac{\text{159.7 g}}{\text{1 mol Fe}_{\text{2}}\text{O}_{3}}=\text{0.640 g } \)
From ChemPRIME: 3.1: Equations and Mass Relationships
References
- ↑ Bowen, N.L.; Schairer, J. F.; Posnjak, E. The Systeme CaO-FeO-SiO2. Am. J. Sci., 5th ser., V. 26, p. 193-284.
- ↑ Lindsley D. H. and Munoz J. L. (1969) Solidus Relations Along The Join Hedenbergite – Ferrosilite. American Journal of Science. Vol. 267-A, pp. 295-324
- ↑ en.Wikipedia.org/wiki/Pyroxene
- ↑ . The equation 2 CaCO3 + Fe2O3 + 2 H2SiO3 → CaFeSi2O6 + 2 CO2 + 2.5 O2 might be preferred by chemists, but geologists often represent syntheses in terms of simple oxides
- ↑ This synthesis is the subject of an student laboratory experiment, "Mineral Synthesis and X-Ray Diffraction Experiments" Perkins, D.; Sorensen, P. in Teaching Mineralogy, Brady, J.B. and Mogk, D.W. Eds., Mineralogy Society of America, Washington, DC, 1997, pp. 81-90.
- ↑ "formula units" is the term used to describe the composition of ionic or network compounds which are not made up of molecules. For example, SiO2 (quartz or sand) is a network crystal made up of Si atoms each with four bridging oxygen atoms to other Si atoms. The ratio is 1 Si: 2 O, even though the structure is made up of SiO4 tetrahedra linked through their vertices.
- ↑ This synthesis is the subject of an student laboratory experiment, "Mineral Synthesis and X-Ray Diffraction Experiments" Perkins, D.; Sorensen, P. in Teaching Mineralogy, Brady, J.B. and Mogk, D.W. Eds., Mineralogy Society of America, Washington, DC, 1997, pp. 81-90.
Contributors and Attributions
Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.


