The Uncertainty Principle
- Page ID
- 50789
It's not surprising if you've heard the Heisenberg Uncertainty Principle mentioned in day-to-day life, and not just in jokes like:
"Werner Heisenberg was driving down the highway and a cop pulled him over. The officer walked up to his window and asked, "Sir, do you know how fast you were going?" Heisenberg replied, "No, but I know where I was"[1]. or bumper stickers like Heisenberg may have slept here
A cultural clue about the meaning of that joke comes from the French electronic music group Telepopmusik, who recorded a song called δp.δq≥h/4π for their album Genetic World (2001). It also goes under the tiltle- L'Incertitude d'Heisenberg which is French for the Heisenberg Uncertainty Principle, or other titles like - Mathematics - Helsinki Central Station which have been posted to YouTube.
The Heisenberg Uncertainty Principle is easily stated mathematically, but it obviously has had a huge impact on our culture and our science. It states that the product of the uncertainty in momentum (P) and the position of a particle cannot be less than a constant expressed in terms of Planck's Constant, h:
\(\Delta X \Delta P \ge \dfrac{h}{4\pi}\)
Here Δ can be taken as the standard deviation, or random uncertainty in measurement. Planck's constant is h = 6.626 x 10-34J s, but the uncertainty principle is sometimes expressed in terms of : \(\hbar\) , which is h/2π:
\(\Delta X \Delta P \ge \dfrac{\hbar}{2}\)
The Uncertainty Principle can be stated in terms of other complementary variables, like energy and time:
\(\Delta E \Delta t \ge \dfrac{\hbar}{2}\)
Example \(\PageIndex{1}\):
Below we'll explore the plausability of the philosophical claim that the Heisenberg Uncertainty Principle allows for free will, if our thoughts are controlled entirely by brain chemistry. Here we'll ask a relevant question: What is the uncertainty in position of the neurotransmitter serotonin (M = 176.215) moving at a velocity of 1 x 10-3 m/s in a 20 nm neural synapse? Assume the concentration of various ions in the synapse make it possible to estimate the velocity to within 10% at best.
Solution: The uncertainty in momentum is Δmv, and if the mass is known with good precision, this is mΔv = 176.215 amu/molecule x 1.66053886 × 10-27kg/amu x 0.10 x 1 x 10-3 m/s = 2.9 x 10-30 kg m s-1
\(\Delta X \Delta P \ge \dfrac{h}{4\pi}\)
\(\Delta X (\text{2.9} \times \text{10}^{-30} \text{kg*m/s} \ge \dfrac{\text{6.626} \times \text{10}^{-34} \text{J s}}{\text{4 (3.14)}}\)
\(\Delta X \ge \text{1.8} \times \text{10}^{-5} \text{m} \)
since this is much larger than the dimensions of a molecule (say 1000 picometers, ~10-9 m), the uncertainty position of the molecule, and the probability that it will dock incorrectly on the receptor nerve, is pretty high.
But the velocity of the molecule, and chemical forces that may more precisely control its velocity and thus docking position, are not known, as should be obvious from this result. If this were literally true, our thoughts and muscular control would be much more random than they are, due to the uncertainty of position of the neurotransmitter. We can think and control motions pretty much without error, so the Heisenberg uncertainty argument for free will (or control of our actions by a god) need to address this issue.
The Observer Effect
The uncertainty principle is related to the observer effect, with which it is often conflated.
The "observer effect" is the change in a phenomenon that the act of observation will make on the phenomenon. For example, a thermometer must absorb some heat to record a temperature, and therefore must reduce the temperature of the matter that is being measured. Another more relevant example is that in order to detect an electron, a photon must first interact with it, and this interaction will change the path of that electron. So to pinpoint the location of an electron, we must change its momentum.
According to the uncertainty principle, even if we draw an analogy between the electron in a box and a billiard ball (Fig. 1a in Wave Mechanics), it will be impossible to determine both the electron’s exact position in the box and its exact speed. Since kinetic energy depends on speed (½ mu2) and Eq. (4) in Wave Mechanics assigns exact values of kinetic energy to the electron in the box, the speed can be calculated accurately. This means that determination of the electron’s position will be very inexact. It will be possible to talk about the probability that the electron is at a specific location, but there will also be some probability of finding it somewhere else in the box. Since it is impossible to know precisely where the electron is at a given instant, the question, “How does it get from one place to another?” is pointless. There is a finite probability that it was at the other place to begin with!
It is possible to be quantitative about the probability of finding a “billiard-ball” electron at a given location, however. Shortly after the uncertainty principle was proposed, the German physicist Max Born (1882 to 1969) suggested that the intensity of the electron wave at any position in the box was proportional to the probability of finding the electron (as a particle) at that same position. Thus if we can determine the shapes of the waves to be associated with an electron, we can also determine the relative probability of its being located at one point as opposed to another. The wave and particle models for the electron are thus connected to and reinforce each other. Niels Bohr suggested the term complementary to describe their relationship. It does no good to ask, “Is the electron a wave or a particle?” Both are ways of drawing an analogy between the microscopic world and macroscopic things whose behavior we understand. Both are useful in our thinking, and they are complementary rather than mutually exclusive.
A graphic way of indicating the probability of finding the electron at a particular location is by the density of shading or stippling along the length of the box. This has been done in Fig. \(\PageIndex{2}\) for the same three electron waves previously illustrated in Fig. 1 from Wave Mechanics. Notice that the density of dots is large wherever the electron wave is large.(This would correspond in the guitar-string analogy to places where the string was vibrating quite far from its rest position.)
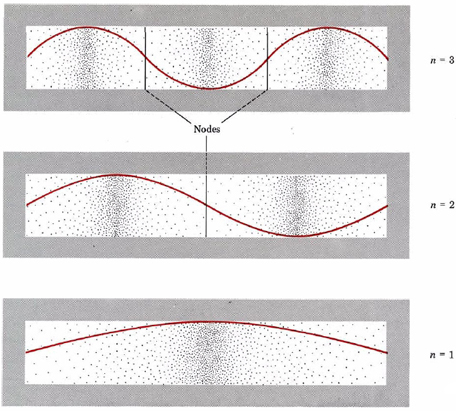
Where the electron wave is small (near the ends of the box in all three cases and at the nodes indicated in the figure), there are only a small number of dots. (A node is a place where the intensity of the wave is zero, that is, in the guitar-string analogy, where the string has not moved from its rest position.)
If the electron is thought of as a wave occupying all parts of the box at once, we can speak of an electron cloud which has greater or lesser density in various parts of the box. There will be a greater quantity of negative charge in a region of high density (a region where there is a greater concentration of dots) than in one of low density. In an atom or molecule, according to the uncertainty principle, the best we can do is indicate electron density in various regions—we cannot locate the precise position of the electron. Therefore electron dot-density diagrams, such as the ones shown in Fig. \(\PageIndex{2}\), give a realistic and useful picture of the behavior of electrons in atoms. In such a diagram the electron density or probability of finding the electron is indicated by the number of dots per unit area. We will encounter electron dot-density diagrams quite often throughout this book. These have all been generated by a computer from accurate mathematical descriptions of the atom or molecule under discussion.
From ChemPRIME: 5.5: The Uncertainty Principle
Contributors and Attributions
Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.