Circular Dichroism

Circular Dichroism, an absorption spectroscopy, uses circularly polarized light to investigate structural aspects of optically active chiral media. It is mostly used to study biological molecules, their structure, and interactions with metals and other molecules.

Introduction

Circular Dichroism (CD) is an absorption spectroscopy method based on the differential absorption of left and right circularly polarized light. Optically active chiral molecules will preferentially absorb one direction of the circularly polarized light. The difference in absorption of the left and right circularly polarized light can be measured and quantified. UV CD is used to determine aspects of protein secondary structure. Vibrational CD, IR CD, is used to study the structure of small organic molecules, proteins and DNA. UV/Vis CD investigates charge transfer transitions in metal-protein complexes.

Circular Polarization of Light

Electromagnetic radiation consists of oscillating electric and magnetic fields perpendicular to each other and the direction of propagation. Most light sources emit waves where these fields oscillate in all directions perpendicular to the propagation vector. Linear polarized light occurs when the electric field vector oscillates in only one plane. In circularly polarized light, the electric field vector rotates around the propagation axis maintaining a constant magnitude. When looked at down the axis of propagation the vector appears to trace a circle over the period of one wave frequency (one full rotation occurs in the distance equal to the wavelength). In linear polarized light the direction of the vector stays constant and the magnitude oscillates. In circularly polarized light the magnitude stays constant while the direction oscillates.

Figure 1: Diagram of linearly polarized and circularly polarized light

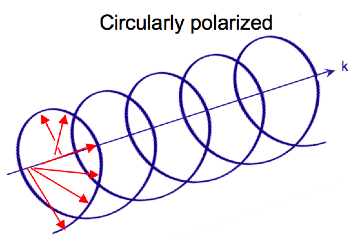
As the radiation propagates the electric field vector traces out a helix. The magnetic field vector is out of phase with the electric field vector by a quarter turn. When traced together the vectors form a double helix.

Light can be circularly polarized in two directions: left and right. If the vector rotates counterclockwise when the observer looks down the axis of propagation, the light is left circularly polarized (LCP). If it rotates clockwise, it is right circularly polarized (RCP). If LCP and RCP of the same amplitude, they are superimposed on one another and the resulting wave will be linearly polarized.

Figure 2: The superposition of LCP and RCP light of the same amplitude produces linearly polarized light

Interaction with Matter

As with linear polarized light, circularly polarized light can be absorbed by a medium. An optically active chiral compound will absorb the two directions of circularly polarized light by different amounts \[ \Delta A = A_l - A_r \]

This can be extended to the Beer-Lambert Law. The molar absorpitivty of a medium will be different for LCP and RCP. The Beer-Lambert Law can be rewritten as \[A = (\varepsilon_l -\varepsilon_r)cl\]

The difference in molar absorptivity is also known as the molar circular dichroism \[\Delta \varepsilon = \varepsilon_l -\varepsilon_r \]

The molar circular dichroism is not only wavelength dependent but also depends on the absorbing molecules conformation, which can make it a function of concentration, temperature, and chemical environment.

Any absorption of light results in a change in amplitude of the incident wave; absorption changes the intensity of the light and intensity of the square of the amplitude. In a chiral medium the molar absorptivities of LCP and RCP light are different so they will be absorbed by the medium in different amounts. This differential absorption results in the LCP and RCP having different amplitudes which means the superimposed light is no longer linearly polarized. The resulting wave is elliptically polarized.

Figure 3: The diagrams of the superposition of LCP and RCP light when viewed down the axis of propagation. On the left the two circular waves (red and green) have the same amplitude which produces linearly polarized light (blue). On the right the LCP (red) has a larger amplitude than the RCP (green), the superposition of the two waves (blue) forms an ellipse.

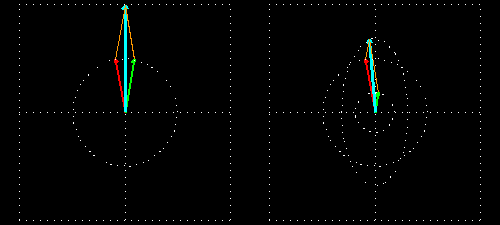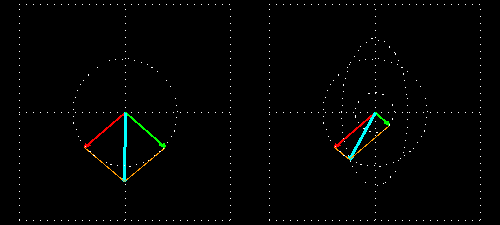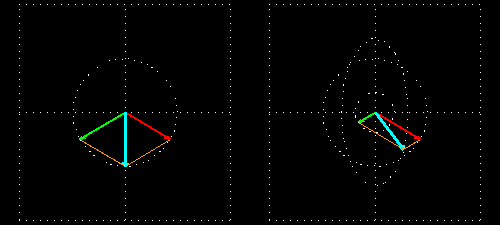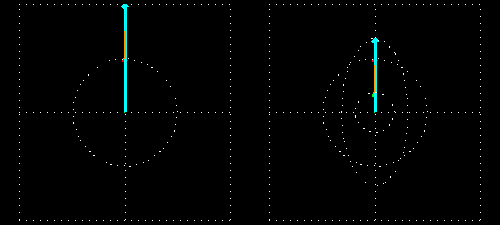
Molar Ellipticity

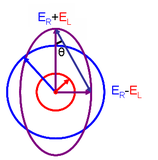
The CD spectrum is often reported in degrees of ellipticity, \(\theta\), which is a measure of the ellipticity of the polarization given by:
\[tan \theta = \frac{E_l-E_r}{E_l+E_r}\]

where E is the magnitude of the electric field vector.

Figure 4: Elliptically polarized light (purple) is the superposition of LCP (red) and RCP (blue) light. \(\theta\) is the angle between the magnitude of the electric field vector at its maximum and its minimum

The change in polarization is usually small and the signal is often measured in radians where \(\theta = \frac{2.303}{4}(A_l - A_r)\) and is a function of wavelength. \(\theta\) can be converted to degrees by multiplying by \(\frac{180}{\pi}\) which gives \(\theta = 32.98 \Delta A\)

The historical reported unit of CD experiments is molar ellipticity, \([\theta]\), which removes the dependence on concentration and path length

\[[\theta] = 3298 \Delta \varepsilon\]

where the 3298 converts from the units of molar absorptivity to the historical units of degrees\(\cdot\) cm²\(\cdot\)dmol^-1.

Applications

Instrumentation

Most commercial CD instruments are based on the modulation techniques introduced by Grosjean and Legrand. Light is linearly polarized and passed through a monochromator. The single wavelength light is then passed through a modulating device, usually a photoelastic modulator (PEM), which transforms the linear light to circular polarized light. The incident light on the sample switches between LCP and RCP light. As the incident light swtches direction of polarization the absorption changes and the differention molar absorptivity can be calculated.

Figure 5: The instrumentation for a common CD spectrometer showing the polarization of light and the differential absorption of LCP and RCP light.

Biological molecules

The most widely used application of CD spectroscopy is identifying structural aspects of proteins and DNA. The peptide bonds in proteins are optically active and the ellipticity they exhibit changes based on the local conformation of the molecule. Secondary structures of proteins can be analyzed using the far-UV (190-250 nm) region of light. The ordered \(\alpha\)-helices, \(\beta\)-sheets, \(\beta\)-turn, and random coil conformations all have characteristic spectra. These unique spectra form the basis for protein secondary structure analysis. It should be noted that in CD only the relative fractions of residues in each conformation can be determined but not specifically where each structural feature lies in the molecule. In reporting CD data for large biomolecules it is necessary to convert the data into a normalized value that is independent of molecular length. To do this the molar ellipticity is divided by the number of residues or monomer units in the molecule.

The real value in CD comes from the ability to show conformational changes in molecules. It can be used to determine how similar a wild type protein is to mutant or show the extent of denaturation with a change in temperature or chemical environment. It can also provide information about structural changes upon ligand binding. In order to interpret any of this information the spectrum of the native conformation must be determined.

Some information about the tertiary structure of proteins can be determined using near-UV spectroscopy. Absorptions between 250-300 nm are due to the dipole orientation and surrounding environment of the aromatic amino acids, phenylalanine, tyrosine, and tryptophan, and cysteine residues which can form disulfide bonds. Near-UV techniques can also be used to provide structural information about the binding of prosthetic groups in proteins.

Metal containing proteins can be studied by visible CD spectroscopy. Visible CD light excites the d-d transitions of metals in chiral environments. Free ions in solution will not absorb CD light so the pH dependence of the metal binding and the stoichiometry can be determined.

Vibrational CD (VCD) spectroscopy uses IR light to determine 3D structures of short peptides, nucleic acids, and carbohydrates. VCD has been used to show the shape and number of helices in A-, B-, and Z-DNA. VCD is still a relatively new technique and has the potential to be a very powerful tool. Resolving the spectra requires extensive ab initio calculations, as well as, high concentrations and must be performed in water, which may force the molecule into a nonnative conformation.

References

1. Woody, R. W. Circular-Dichroim. Methods in Enzymology 246, 34-71 (1995).
2. Johnson, W. C. Protein secondary structure and circular dichroism: A practical guide. Proteins: Structure, Function, and Genetics 7, 205–214 (1990).
3. Drake, A. F. Polarisation modulation-the measurement of linear and circular dichroism. Journal of Physics E: Scientific Instruments 19, 170–181 (1986).
4. Neidig, M. L., Wecksler, A. T., Schenk, G., Holman, T. R. & Solomon, E. I. Kinetic and spectroscopic studies of N694C lipoxygenase:  a probe of the substrate activation mechanism of a nonheme ferric enzyme. Journal of the American Chemical Society 129, 7531–7537 (2007).
5. Polavarapu, P. L. & Zhao, C. X. Vibrational circular dichroism: a new spectroscopic tool for biomolecular structural determination. Fresenius Journal Anaytical Chemistry 366, 727–734 (2000).