Crystal Field Stabilization Energy
- Page ID
- 15736
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A consequence of Crystal Field Theory is that the distribution of electrons in the d orbitals may lead to net stabilization (decrease in energy) of some complexes depending on the specific ligand field geometry and metal d-electron configurations. It is a simple matter to calculate this stabilization since all that is needed is the electron configuration and knowledge of the splitting patterns.
The Crystal Field Stabilization Energy is defined as the energy of the electron configuration in the ligand field minus the energy of the electronic configuration in the isotropic field.
\[CFSE=\Delta{E}=E_{\text{ligand field}} - E_{\text{isotropic field}} \label{1} \]
The CSFE will depend on multiple factors including:
- Geometry (which changes the d-orbital splitting patterns)
- Number of d-electrons
- Spin Pairing Energy
- Ligand character (via Spectrochemical Series)
For an octahedral complex, an electron in the more stable \(t_{2g}\) subset is treated as contributing \(-2/5\Delta_o\) whereas an electron in the higher energy \(e_g\) subset contributes to a destabilization of \(+3/5\Delta_o\). The final answer is then expressed as a multiple of the crystal field splitting parameter \(\Delta_o\). If any electrons are paired within a single orbital, then the term \(P\) is used to represent the spin pairing energy.
What is the Crystal Field Stabilization Energy for a high spin \(d^7\) octahedral complex?
Solution
The splitting pattern and electron configuration for both isotropic and octahedral ligand fields are compared below.

The energy of the isotropic field \((E_{\text{isotropic field}}\)) is
\[ E_{\text{isotropic field}}= 7 \times 0 + 2P = 2P \nonumber \]
The energy of the octahedral ligand field \(E_{\text{ligand field}}\) is
\[E_{\text{ligand field}} = (5 \times -2/5 \Delta_o ) + (2 \times 3/5 \Delta_o) + 2P = -4/5 \Delta_o + 2P \nonumber \]
So via Equation \ref{1}, the CFSE is
\[\begin{align} CFSE &=E_{\text{ligand field}} - E_{\text{isotropic field}} \nonumber \\[4pt] &=( -4/5\Delta_o + 2P ) - 2P \nonumber \\[4pt] &=-4/5 \Delta_o \nonumber \end{align} \nonumber \]
Notice that the Spin pairing Energy falls out in this case (and will when calculating the CFSE of high spin complexes) since the number of paired electrons in the ligand field is the same as that in isotropic field of the free metal ion.
What is the Crystal Field Stabilization Energy for a low spin \(d^7\) octahedral complex?
Solution
The splitting pattern and electron configuration for both isotropic and octahedral ligand fields are compared below.

The energy of the isotropic field is the same as calculated for the high spin configuration in Example 1:
\[ E_{\text{isotropic field}}= 7 \times 0 + 2P = 2P \nonumber \]
The energy of the octahedral ligand\) field \(E_{\text{ligand field}}\) is
\[\begin{align} E_{\text{ligand field}} &= (6 \times -2/5 \Delta_o ) + (1 \times 3/5 \Delta_o) + 3P \nonumber \\[4pt] &= -9/5 \Delta_o + 3P \nonumber \end{align} \nonumber \]
So via Equation \ref{1}, the CFSE is
\[\begin{align} CFSE&=E_{\text{ligand field}} - E_{\text{isotropic field}} \nonumber \\[4pt] &=( -9/5 \Delta_o + 3P ) - 2P \nonumber \\[4pt] &=-9/5 \Delta_o + P \nonumber \end{align} \nonumber \]
Adding in the pairing energy since it will require extra energy to pair up one extra group of electrons. This appears more a more stable configuration than the high spin \(d^7\) configuration in Example \(\PageIndex{1}\), but we have then to take into consideration the Pairing energy \(P\) to know definitely, which varies between \(200-400\; kJ\; mol^{-1}\) depending on the metal.
| Total d-electrons | Isotropic Field | Octahedral Complex | Crystal Field Stabilization Energy | ||||
|---|---|---|---|---|---|---|---|
| High Spin | Low Spin | ||||||
| \(E_{\text{isotropic field}}\) | Configuration | \(E_{\text{ligand field}}\) | Configuration | \(E_{\text{ligand field}}\) | High Spin | Low Spin | |
| d0 | 0 | \(t_{2g}\)0\(e_g\)0 | 0 | \(t_{2g}\)0\(e_g\)0 | 0 | 0 | 0 |
| d1 | 0 | \(t_{2g}\)1\(e_g\)0 | -2/5 \(\Delta_o\) | \(t_{2g}\)1\(e_g\)0 | -2/5 \(\Delta_o\) | -2/5 \(\Delta_o\) | -2/5 \(\Delta_o\) |
| d2 | 0 | \(t_{2g}\)2\(e_g\)0 | -4/5 \(\Delta_o\) | \(t_{2g}\)2\(e_g\)0 | -4/5 \(\Delta_o\) | -4/5 \(\Delta_o\) | -4/5 \(\Delta_o\) |
| d3 | 0 | \(t_{2g}\)3\(e_g\)0 | -6/5 \(\Delta_o\) | \(t_{2g}\)3\(e_g\)0 | -6/5 \(\Delta_o\) | -6/5 \(\Delta_o\) | -6/5 \(\Delta_o\) |
| d4 | 0 | \(t_{2g}\)3\(e_g\)1 | -3/5 \(\Delta_o\) | \(t_{2g}\)4\(e_g\)0 | -8/5 \(\Delta_o\) + P | -3/5 \(\Delta_o\) | -8/5 \(\Delta_o\) + P |
| d5 | 0 | \(t_{2g}\)3\(e_g\)2 | 0 \(\Delta_o\) | \(t_{2g}\)5\(e_g\)0 | -10/5 \(\Delta_o\) + 2P | 0 \(\Delta_o\) | -10/5 \(\Delta_o\) + 2P |
| d6 | P | \(t_{2g}\)4\(e_g\)2 | -2/5 \(\Delta_o\) + P | \(t_{2g}\)6\(e_g\)0 | -12/5 \(\Delta_o\) + 3P | -2/5 \(\Delta_o\) | -12/5 \(\Delta_o\) + P |
| d7 | 2P | \(t_{2g}\)5\(e_g\)2 | -4/5 \(\Delta_o\) + 2P | \(t_{2g}\)6\(e_g\)1 | -9/5 \(\Delta_o\) + 3P | -4/5 \(\Delta_o\) | -9/5 \(\Delta_o\) + P |
| d8 | 3P | \(t_{2g}\)6\(e_g\)2 | -6/5 \(\Delta_o\) + 3P | \(t_{2g}\)6\(e_g\)2 | -6/5 \(\Delta_o\) + 3P | -6/5 \(\Delta_o\) | -6/5 \(\Delta_o\) |
| d9 | 4P | \(t_{2g}\)6\(e_g\)3 | -3/5 \(\Delta_o\) + 4P | \(t_{2g}\)6\(e_g\)3 | -3/5 \(\Delta_o\) + 4P | -3/5 \(\Delta_o\) | -3/5 \(\Delta_o\) |
| d10 | 5P | \(t_{2g}\)6\(e_g\)4 | 0 \(\Delta_o\) + 5P | \(t_{2g}\)6\(e_g\)4 | 0 \(\Delta_o\) + 5P | 0 | 0 |
\(P\) is the spin pairing energy and represents the energy required to pair up electrons within the same orbital. For a given metal ion P (pairing energy) is constant, but it does not vary with ligand and oxidation state of the metal ion).
Octahedral Preference
Similar CFSE values can be constructed for non-octahedral ligand field geometries once the knowledge of the d-orbital splitting is known and the electron configuration within those orbitals known, e.g., the tetrahedral complexes in Table \(\PageIndex{2}\). These energies geoemtries can then be contrasted to the octahedral CFSE to calculate a thermodynamic preference (Enthalpy-wise) for a metal-ligand combination to favor the octahedral geometry. This is quantified via a Octahedral Site Preference Energy defined below.
The Octahedral Site Preference Energy (OSPE) is defined as the difference of CFSE energies for a non-octahedral complex and the octahedral complex. For comparing the preference of forming an octahedral ligand field vs. a tetrahedral ligand field, the OSPE is thus:
\[OSPE = CFSE_{(oct)} - CFSE_{(tet)} \label{2} \]
The OSPE quantifies the preference of a complex to exhibit an octahedral geometry vs. a tetrahedral geometry.

Note: the conversion between \(\Delta_o\) and \(\Delta_t\) used for these calculations is:
\[\Delta_t \approx \dfrac{4}{9} \Delta_o \label{3} \]
which is applicable for comparing octahedral and tetrahedral complexes that involve same ligands only.
| Total d-electrons | CFSE(Octahedral) | CFSE(Tetrahedral) | OSPE (for high spin complexes)** | ||
|---|---|---|---|---|---|
| High Spin | Low Spin | Configuration | Always High Spin* | ||
| d0 | 0 \(\Delta_o\) | 0 \(\Delta_o\) | e0 | 0 \(\Delta_t\) | 0 \(\Delta_o\) |
| d1 | -2/5 \(\Delta_o\) | -2/5 \(\Delta_o\) | e1 | -3/5 \(\Delta_t\) | -6/45 \(\Delta_o\) |
| d2 | -4/5 \(\Delta_o\) | -4/5 \(\Delta_o\) | e2 | -6/5 \(\Delta_t\) | -12/45 \(\Delta_o\) |
| d3 | -6/5 \(\Delta_o\) | -6/5 \(\Delta_o\) | e2t21 | -4/5 \(\Delta_t\) | -38/45 \(\Delta_o\) |
| d4 | -3/5 \(\Delta_o\) | -8/5 \(\Delta_o\) + P | e2t22 | -2/5 \(\Delta_t\) | -19/45 \(\Delta_o\) |
| d5 | 0 \(\Delta_o\) | -10/5 \(\Delta_o\) + 2P | e2t23 | 0 \(\Delta_t\) | 0 \(\Delta_o\) |
| d6 | -2/5 \(\Delta_o\) | -12/5 \(\Delta_o\) + P | e3t23 | -3/5 \(\Delta_t\) | -6/45 \(\Delta_o\) |
| d7 | -4/5 \(\Delta_o\) | -9/5 \(\Delta_o\) + P | e4t23 | -6/5 \(\Delta_t\) | -12/45 \(\Delta_o\) |
| d8 | -6/5 \(\Delta_o\) | -6/5 \(\Delta_o\) | e4t24 | -4/5 \(\Delta_t\) | -38/45 \(\Delta_o\) |
| d9 | -3/5 \(\Delta_o\) | -3/5 \(\Delta_o\) | e4t25 | -2/5 \(\Delta_t\) | -19/45 \(\Delta_o\) |
| d10 | 0 | 0 | e4t26 | 0 \(\Delta_t\) | 0 \(\Delta_o\) |
\(P\) is the spin pairing energy and represents the energy required to pair up electrons within the same orbital.
Tetrahedral complexes are always high spin since the splitting is appreciably smaller than \(P\) (Equation \ref{3}).
After conversion with Equation \ref{3}. The data in Tables \(\PageIndex{1}\) and \(\PageIndex{2}\) are represented graphically by the curves in Figure \(\PageIndex{1}\) below for the high spin complexes only. The low spin complexes require knowledge of \(P\) to graph.

- The OSPE is small in \(d^1\), \(d^2\), \(d^5\), \(d^6\), \(d^7\) complexes and other factors influence the stability of the complexes including steric factors
- The OSPE is large in \(d^3\) and \(d^8\) complexes which strongly favor octahedral geometries
Applications
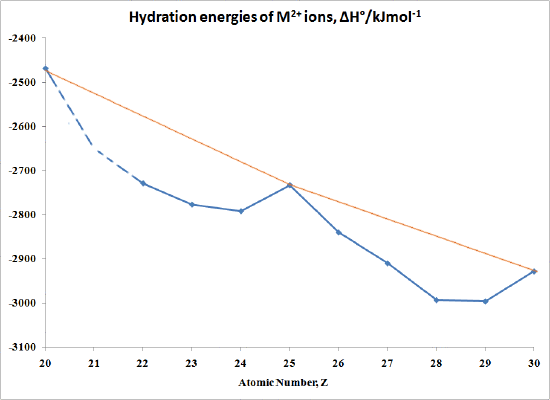
The "double-humped" curve in Figure \(\PageIndex{1}\) is found for various properties of the first-row transition metals, including Hydration and Lattice energies of the M(II) ions, ionic radii as well as the stability of M(II) complexes. This suggests that these properties are somehow related to Crystal Field effects.
In the case of Hydration Energies describing the complexation of water ligands to a bare metal ion:
\[M^{2+} (g) + H_2O \rightarrow [M(OH_2)_6]^{2+} (aq) \nonumber \]
Table \(\PageIndex{3}\) and Figure \(\PageIndex{1}\) shows this type of curve. Note that in any series of this type not all the data are available since a number of ions are not very stable in the M(II) state.
| M | ΔH°/kJmol-1 | M | ΔH°/kJmol-1 |
|---|---|---|---|
| Ca | -2469 | Fe | -2840 |
| Sc | no stable 2+ ion | Co | -2910 |
| Ti | -2729 | Ni | -2993 |
| >V | -2777 | Cu | -2996 |
| Cr | -2792 | Zn | -2928 |
| Mn | -2733 |
Contributors and Attributions
Prof. Robert J. Lancashire (The Department of Chemistry, University of the West Indies)

