6.1: Internal Energy

Defining the System

Chemists are interested in systems containing matter—that which has mass and occupies physical space. Classical thermodynamics looks at macroscopic aspects of matter. It deals with the properties of aggregates of vast numbers of microscopic particles (molecules, atoms, and ions). The macroscopic viewpoint, in fact, treats matter as a continuous material medium rather than as the collection of discrete microscopic particles we know are actually present. Although this e-book is an exposition of classical thermodynamics, at times it will point out connections between macroscopic properties and molecular structure and behavior.

A thermodynamic system is any three-dimensional region of physical space on which we wish to focus our attention. Usually we consider only one system at a time and call it simply “the system.” The rest of the physical universe constitutes the surroundings of the system.

The boundary is the closed three-dimensional surface that encloses the system and separates it from the surroundings. The boundary may (and usually does) coincide with real physical surfaces: the interface between two phases, the inner or outer surface of the wall of a flask or other vessel, and so on. Alternatively, part or all of the boundary may be an imagined intangible surface in space, unrelated to any physical structure. The size and shape of the system, as defined by its boundary, may change in time. In short, our choice of the three-dimensional region that constitutes the system is arbitrary—but it is essential that we know exactly what this choice is.

We usually think of the system as a part of the physical universe that we are able to influence only indirectly through its interaction with the surroundings, and the surroundings as the part of the universe that we are able to directly manipulate with various physical devices under our control. That is, we (the experimenters) are part of the surroundings, not the system.

For some purposes we may wish to treat the system as being divided into subsystems, or to treat the combination of two or more systems as a supersystem.

If over the course of time matter is transferred in either direction across the boundary, the system is open. If no matter is transferred into or out of the system, the system is closed. If the system is open, matter may pass through a stationary boundary, or the boundary may move through matter that is fixed in space.

Note

One difficulty in describing energy exchange is the fact that heat is not an object; it is the process of energy transfer because of a temperature difference. However, it often difficult to word statements so that heat does not sound like an entity. So, although it is preferable to write that that a system has "heated up", you will often read that a system "gained heat" or "gained energy in the form of heat".

Both open and closed systems can transfer energy in either direction across the boundary if the boundary allows such an energy transfer. A boundary that allows heat exchanges is called diathermal or diathermic. An adiabatic (Greek: impassable) boundary, on the other hand, is a boundary that does not allow heat transfer. We can, in principle, ensure that the boundary is adiabatic by surrounding the system with an adiabatic wall—one with perfect thermal insulation and a perfect radiation shield. An isolated system is one that exchanges no matter, heat, or work with the surroundings, so that the mass and total energy of the system remain constant over time. A closed system with an adiabatic boundary, constrained to do no work and to have no work done on it, is an isolated system.

In chemistry, systems can undergo changes in heat because of changes in the number and types of bonds, as well as changes in the type and effectiveness of intermolecular forces. Any process that results in the heating of the system is called an exothermic process. These processes occur when the energy released by the formation of new bonds and intermolecular forces is greater than the energy taken in by the breaking of existing bonds and intermolecular forces. When a system undergoes an exothermic process, its temperature will increase. If held in an adiabatic container, the system will maintain this increased temperature indefinitely. If held in a diathermic container, the system will lose heat to the surroundings until the temperatures are once again in thermal equilibrium.

Any process that results in the cooling of the system is called an endothermic process. These processes occur when the energy released by the formation of new bonds and intermolecular forces is less than the energy taken in by the breaking of existing bonds and intermolecular forces. When a system undergoes an endothermic process, its temperature will decrease. If held in an adiabatic container, the system will maintain this decreased temperature indefinitely. If held in a diathermic container, the system will gain heat from the surroundings until the temperatures are once again in thermal equilibrium.

The constraints required to prevent work usually involve forces between the system and surroundings. In that sense a system may interact with the surroundings even though it is isolated. For instance, a gas contained within rigid, thermally-insulated walls is an isolated system. However, the gas exerts a force on each wall, and the walls exert an equal and opposite force on the gas. An isolated system may also experience a constant external field, such as a gravitational field.

Heat

Thermal energy is kinetic energy associated with the random motion of atoms and molecules. Temperature is a quantitative measure of “hot” or “cold.” When the atoms and molecules in an object are moving or vibrating quickly, they have a higher average kinetic energy (KE), and we say that the object is “hot.” When the atoms and molecules are moving slowly, they have lower KE, and we say that the object is “cold” (Figure \(\PageIndex{1}\)). Assuming that no chemical reaction or phase change (such as melting or vaporizing) occurs, increasing the amount of thermal energy in a sample of matter will cause its temperature to increase. And, assuming that no chemical reaction or phase change (such as condensation or freezing) occurs, decreasing the amount of thermal energy in a sample of matter will cause its temperature to decrease.

'

Figure \(\PageIndex{1}\): (a) The molecules in a sample of water at a higher temperature move more rapidly than (b) those in a sample of water at a lower temperature.

Work

Work is the purposeful, or organized, transfer of energy associated with the non-random motion of atoms and molecules. On a macroscopic scale, we describe work as the result of a force moving an object. In other words, the energy is expended in an organized, coordinated fashion to make an object move. This same concept can be applied on the molecular level to describe the coordinated movement of molecules and atoms as work.

Figure \(\PageIndex{2}\): Pressure·Volume Work by Gas Particles. Using a frictionless piston, if the external pressure is less than P_int (a), the gas molecules with an upward component to their motion will collide with the piston, collectively forcing the piston to move upward. The final volume (V_f) will be greater than V_i. Alternatively, if the external pressure is greater than P_int (b), the piston will perform work on the gas particles as it causes them to collectively gain a downward component to their motion.The final volume (V_f) will be less than V_i.

Internal Energy

The First Law, Part 1

The state of a system is a complete description of a system at a given time, including its temperature and pressure, the amount of matter it contains, its chemical composition, and the physical state of the matter. A state function is a property of a system whose magnitude depends on only the present state of the system, not its previous history. Temperature, pressure, volume, and potential energy are all state functions. The temperature of an oven, for example, is independent of however many steps it may have taken for it to reach that temperature. Similarly, the pressure in a tire is independent of how often air is pumped into the tire for it to reach that pressure, as is the final volume of air in the tire. Heat and work, on the other hand, are not state functions because they are path dependent. For example, a car sitting on the top level of a parking garage has the same potential energy whether it was lifted by a crane, set there by a helicopter, driven up, or pushed up by a group of students (Figure \(\PageIndex{3}\)). The amount of work expended to get it there, however, can differ greatly depending on the path chosen. If the students decided to carry the car to the top of the ramp, they would perform a great deal more work than if they simply pushed the car up the ramp (unless, of course, they neglected to release the parking brake, in which case the work expended would increase substantially!). The potential energy of the car is the same, however, no matter which path they choose.

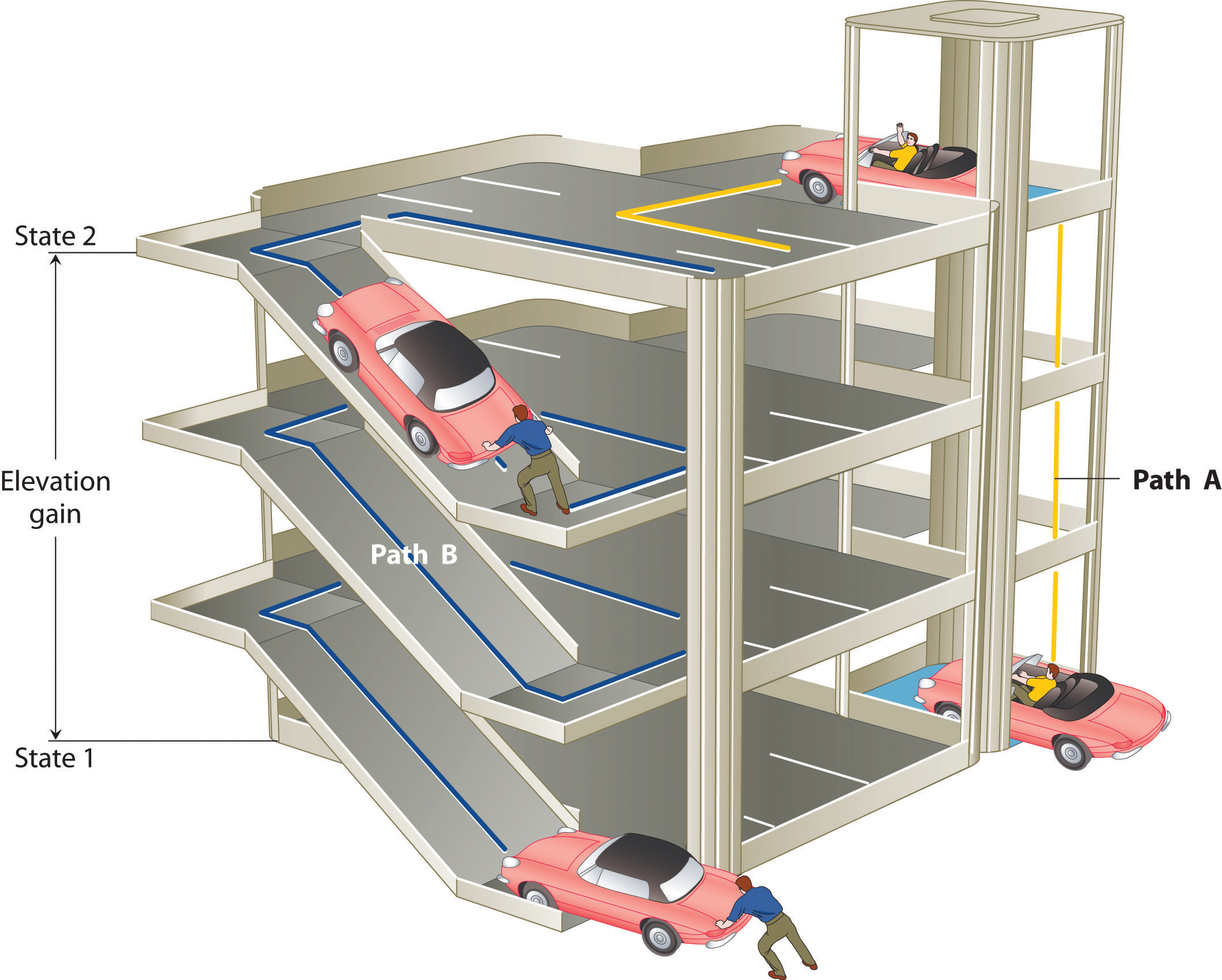
Figure \(\PageIndex{3}\): Elevation as an Example of a State Function. The change in elevation between state 1 (at the bottom of the parking garage) and state 2 (at the top level of the parking garage) is the same for both paths A and B; it does not depend on which path is taken from the bottom to the top. In contrast, the distance traveled and the work needed to reach the top do depend on which path is taken. Elevation is a state function, but distance and work are not state functions.

The relationship between the energy change of a system and that of its surroundings is given by the first law of thermodynamics, which states that the energy of the universe is constant. We can express this law mathematically as follows:

\[U_{univ}=ΔU_{sys}+ΔU_{surr}=0 \label{2.1.1}\]

\[\Delta{U_{sys}}=−ΔU_{surr} \label{2.1.2}\]

where the subscripts univ, sys, and surr refer to the universe, the system, and the surroundings, respectively. Thus \(ΔU_{sys}\), the change in internal energy of a system, is identical in magnitude but opposite in sign to the change in energy of its surroundings.

(\(ΔU_{sys}\)) is independent of the path taken and is therefore a state function. Thus \(ΔU_{sys}\) also can be expressed as:

\[ΔU_{sys} = U_{final} - U_{initial} \label{2.1.3}\]

Because we focus almost exclusively on the changes in the energy of a system, we will not use “sys” as a subscript unless we need to distinguish explicitly between a system and its surroundings. It should also be noted that \(ΔU_{sys}\) is an extensive property that changes with the amount of substance present. A related, intensive property is the molar internal energy, \(U_m\), defined as

\[U_m = \dfrac{U}{n}\label{2.1.4}\]

Contributions to Internal Energy

Internal energy can be explained on a molecular level by taking into account the various terms that can contribute to this total energy. This accounting process is easiest to carry out for a perfect gas sample because the particles do not interact with each other. The internal energy of a perfect gas can thus be approximated by adding the contributions of the zero-point energy, the translational energy, rotational energy, vibrational energy, and electronic energy. The translational and rotational energy contributions involve the most straightforward calculations because for these terms, each degree of freedom contributes \(\dfrac{1}{2}RT\) to the molar internal energy according to the equipartion theorem. Thus, the translational contribution for all particles is \(\dfrac{3}{2}RT\) for movement in the x, y and z directions. The rotational contribution depends on the number of atoms in the particle. Single atoms have no rotational degrees of freedom. Linear molecules have 2 degrees of freedom (along the two axes perpendicular to the bond axis. Polyatomic, nonlinear molecules all have three degrees of rotational freedom.

It is important to note that the internal energy of a sample of a perfect gas is independent of the volume occupied by the gas particles. There are no intermolecular attractions between the particles, so there is no difference in potential energy if the particles are very close together in a small container, or very far apart in a large container.

The internal energy of real gases, liquids, and solids cannot be so simply described because the particles do experience intermolecular forces of attraction, and thus there is a contribution of their potential energy to the total internal energy. It is still true, however, that as the temperature increases the internal energy increases because the likelihood of having higher-energy translational and rotational energy levels increases.

The First Law, Part 2

Because heat and work are the only two ways in which energy can be transferred between a system and its surroundings, any change in the internal energy of the system is the sum of the heat transferred (q) and the work done (w):

\[ΔU_{sys} = q + w \label{2.1.5}\]

Assuming the universe is an isolated system, the second law can be reworded as:

Definition

The internal energy of an isolated system is constant. Thus, q = 0 and w = 0 for an isolated system, just as the definition demands.

For a closed system, energy can be transferred into and out of the system. By convention, the \(q\) and \(w\) terms in Equation \(\ref{2.1.5}\) are assigned negative values if energy leaves the system (an exothermic process, or work is done by the system), and assigned positive values if energy enters the system (an endothermic process, or work is done on the system.)

Example \(\PageIndex{1}\):

Suppose that 150 kJ of work are used to compress a spring, and that 25 kJ of heat are given off by the spring during this compression. What is the change in internal energy of the spring during the process?

Strategy: Use \(ΔU_{sys} = q + w \) to solve for \(\Delta U_{sys}\) with the understanding that work is done on the system (+ w) and heat is lost from the system (- q).

Answer: \(\Delta U_{sys}\) = 150 kJ - 25 kJ = + 125 kJ.

Exercise \(\PageIndex{1}\)

Suppose that 100 kJ of work is done by a motor, but that it also gives off 10 kJ of heat while carrying out this work. What is the change in internal energy of the motor during the process?

Answer: \(\Delta U_{sys}\) = -100 kJ - 10 kJ = - 110 kJ.

Expansion/Compression Work

Work in general is defined as a product of a force \(\textbf{F}\) and a path element \(\textbf{ds}\). Both are vectors and work is computed by integrating over their product

\[w = \int \textbf{F} \cdot \textbf{ds}\label {2.1.6}\]

Moving an object against the force of friction is but one example of work.

\[w_{friction} = \int \textbf{F}_{friction} \cdot \textbf{ds}\label{2.1.7}\]

We could also think of electrical work. In that case we would be moving a charge e (e.g. the negative charge of an electron) against an electrical (vector) field \(\textbf{E}\). The work would be:

\[w_{electical} = \int e \textbf{E} \cdot \textbf{ds}\label{2.1.8}\]

Other examples are the stretching of a rubber band against the elastic force or moving a magnet in a magnetic field etc, etc.

In the case of a cylinder filled with a perfect gas, we can introduce the area of the piston A and forget about the vectorial nature. The movement of the piston is constrained to one direction, the one in which we apply an external pressure, P_ex. Recall that P is force (F) per area (A). We can also assume that the molecules of the gas rapidly equilibrate to the applied pressure and make it into an all-sided phenomenon.

\[w_{volume} = \int \left(\dfrac{F}{\cancel{A}} \right)(\cancel{A}\,ds) = \int P_{ex}\,dV \label{2.1.9}\]

This particular form of work is called volume work and will play an important role in the development of our theory. Notice however that volume work is only one form of work.

conventions

It is important to create a sign convention at this point: positive heat and positive work are always what you put in into the system. If the system happens to give off heat or to do work, these events get a minus sign.

In other words: you pay the bill.

To comply with this convention we need to rewrite volume work (Equation \(\ref{2.1.9}\)) as

\[w_{volume} = - \int \left( \dfrac{F}{\cancel{A}} \right) (\cancel{A}\,ds) = - \int P_{ex}\,dV \label{2.1.10}\]

Hence, to decrease the volume of the gas (\(\Delta V\) is negative), we must do work on the gas. This is a gain of energy by the system, so the sign of the work is positive. If the volume of the gas increases, work must be done by the gas to move the piston. This is a loss of energy from the system, and so the sign of the work is negative.

Irreversible Expansion/Contraction against a Constant Pressure

When a system is far from equilibrium, an infinitesimal change in any variable will be insignificant because at least one variable in the system will be undergoing a relatively large change as the system drives toward equilibrium. Because the system is far from equilibrium, the significant change(s) that occur as the system attains equilibrium are considered irreversible changes, not only because they are not easily undone, but also because to undo them would drive the system away from equilibrium. Such a situation occurs when starting materials in a chemical reaction are mixed together, when a very hot object is set next to a cold object, and when a 50 kilogram mass is placed on a piston that was in equilibrium with a gas sample that was at one atmosphere pressure.

If a gas expands against a constant pressure (atmospheric pressure or a constant mass set on the piston), Equation \(\ref{2.1.10}\) can be simplified to

\[w = -P_{ex}\, \int dV = -P_{ex}(V_{final} - V_{initial}) = -P_{ex}\Delta V\label{2.1.11}\]

Because integrals can be interpreted as an area under a curve, the value of \(w\) is equal to the area under the constant pressure line, \(P = P_{ex}\) between \(V_{initial}\) and \(V_{final}\). Figure \(\PageIndex{4}\) shows a PV graph (known as an indicator graph)of a constant pressure expansion.

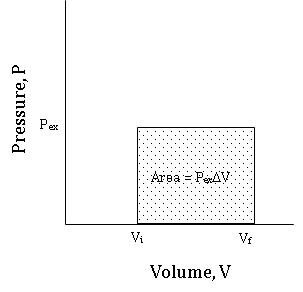
Figure \(\PageIndex{4}\): An indicator graph for a constant pressure expansion

This type of indicator graph could be obtained by adding energy to a gas sample, held in a cylinder by a piston that is exerting a constant pressure. The cylinder would need to have diathermal walls, and must be surrounded by a constant temperature bath. The initial state of this expansion is not stable, because the pressure of the gas, P_gas, must be quite different than the external pressure, P_ex. If you want the gas to undergo an expansion, P_gas > P_ex. If you want the gas to undergo a compression, P_gas < P_ex. For both processes, the piston must be held in place initially until you are ready to start the process. It is also true that in both compression and expansion, the process will continue until P_gas = P_ex. For the isothermal expansion, the energy needed for the expansion work will be delivered into the system by the surrounding constant temperature bath. For the isothermal compression, the heat created when the work is done on the system will be dissipated into the surrounding constant temperature bath.

Figure \(\PageIndex{5}\): An system undergoing a constant pressure expansion. The mass exerting the pressure is a fixed value, so P_ex is constant.

If the gas expands with no opposing force, then P_ex must be 0 and thus \(w\) must be 0. This special case of expansion is called free expansion, and occurs whenever a gas expands into a vacuum.

Example \(\PageIndex{2}\):

Suppose 3.00 moles of an perfect gas held in a 4.00 L container at 20.0 bar undergoes an irreversible, isothermal expansion against a constant external pressure of 5.00 bar. How much work was done by the gas?

Strategy: You need to use Equation \(\ref{2.1.11}\) to solve the Equation. You know P_ex and \(V_i\), so you must first find the \(V_f\) of the gas. To do so, you need to find the T of the gas, using PV=nRT.

Answer:

\(T = \dfrac{P_i·V_i}{nR} = \dfrac{(20.0 bar)(4.00 L)}{(3.00 moles)(0.08314 \dfrac{bar·L}{mole·K})} = 321 K\)

\(V_f = \dfrac{nRT}{P_f} = \dfrac{(3.00 moles)(0.08314 \dfrac{bar·L}{mole·K})(321 K)}{5.00 bar} = 16.0 L\)

\(w_{irreversible} = -P_{ex}\Delta V = - 5.00 bar\, x\, \dfrac {10^5 Pa}{bar} \, x\, (16.0 L - 4.00 L)\, x\, \dfrac{10^{-3}m^3}{L} = - 6.00 x 10^3 J\)

Exercise \(\PageIndex{2}\)

A. Suppose 2.50 moles of an perfect gas held in a 2.00 L container at 10.0 bar undergoes an irreversible, isothermal expansion against a constant external pressure of 2.00 bar. How much work was done by the gas?

B. Suppose 2.50 moles of an perfect gas held in a 2.00 L container at 10.0 bar undergoes three, separate irreversible, isothermal expansions. The first step involves an expansion against a P_ex of 6.00 bar. The second step involves an expansion against a P_ex of 3.00 bar. The third step involves an expansion against a P_ex of 2.00 bar. How much total work was done by the gas over the three combined steps?

Answer: A. -1.60 x 10³ J B. -2.47 x 10³ J

Notice that the final state in part B is the same as the final state in part A. However, the work done by the gas increased when the number of irreversible steps increased.

Example \(\PageIndex{3}\)

A sample of an ideal gas in the cylinder of an engine is compressed from 400 mL to 50.0 mL during the compression stroke against a constant pressure of 8.00 atm. At the same time, 140 J of energy is transferred from the gas to the surroundings as heat. What is the total change in the internal energy (ΔU) of the gas in joules?

Given: initial volume, final volume, external pressure, and quantity of energy transferred as heat

Asked for: total change in internal energy

Strategy:

1. Determine the sign of \(q\) to use in Equation \(\ref{2.1.5}\).
2. From Equation \(\ref{2.1.11}\) calculate \(w\) from the values given. Substitute this value into Equation \(\ref{2.1.5}\) to calculate \(ΔU\).

Solution

A. From Equation \(\ref{2.1.5}\), we know that ΔU = q + w. We are given the magnitude of q (140 J) and need only determine its sign. Because energy is transferred from the system (the gas) to the surroundings, q is negative by convention.

B Because the gas is being compressed, we know that work is being done on the system, so \(w\) must be positive. From Equation \(\ref{2.1.11}\),

\(w=-P_{\textrm{ext}}\Delta V=-8.00\textrm{ atm}(\textrm{0.0500 L} - \textrm{0.400 L})\left(\dfrac{\textrm{101.3 J}}{\mathrm{L\cdot atm}} \right)=284\textrm{ J}\)

Thus

ΔU = q + w = −140 J + 284 J = 144 J

In this case, although work is done on the gas, increasing its internal energy, heat flows from the system to the surroundings, decreasing its internal energy by 144 J. The work done and the heat transferred can have opposite signs.

Exercise \(\PageIndex{3}\)

A sample of an ideal gas is allowed to expand from an initial volume of 0.200 L to a final volume of 3.50 L against a constant external pressure of 0.995 atm. At the same time, 117 J of heat is transferred from the surroundings to the gas. What is the total change in the internal energy (ΔU) of the gas in joules?

Answer:

−216 J

Reversible Expansion/Contraction

When a system is at equilibrium, an infinitesimal change in any variable will cause the system to change infinitesimally to attain a new equilibrium. From this new equilibrium, a further infinitesimal change would cause the system to change infinitesimally once again to attain a new equilibrium, which could, in fact, be the original equilibrium state. Because the system is always at or infinitesimally close to equilibrium, all of the infinitesimal changes are considered reversible changes because any given change can be undone by one or more further infinitesimal changes. Such a situation can occur for a reaction at chemical equilibrium, for an object in thermal equilibrium with its surroundings, and for a gas held in a cylinder by a piston in mechanical equilibrium with the external pressure. A perfectly reversible process, also known as a quasi-static process, would never actually finish, yet we can use the concept to determine the limiting result for many thermodynamic processes.

As was just noted, we can approximate a reversible expansion with a gas sample held in a cylinder by a piston. If the pressure of the gas is equal to the external pressure on the piston, the system is in mechanical equilibrium with the surroundings. If the pressures are equal, then P_ex = P_gas, and Equation \(\ref{2.1.10}\) can be expressed as

\[w = -\int P_{gas}\,dV \label{2.1.12}\]

Isothermal Reversible Expansion/Contraction

Suppose we have a sample of a perfect gas held under pressure in a cylinder by a piston that can be moved in infinitesimally small increments by a motor. The cylinder has diathermal walls, and is submerged in a constant temperature bath. As will be shown in an upcoming section of this chapter, if there is no change in temperature for a perfect gas, there can be no change in internal energy. Thus, for an isothermal process carried out on/by an perfect gas:

\[\Delta U = 0 = q + w\label{2.1.13}\]

Inside the cylinder is a coil that adds heat to the gas sample. The constant temperature bath keeps the gas sample at a constant temperature, so the added heat cannot raise the temperature of the gas. If the temperature of the gas does not change, there is no change in internal energy. If there is no change in internal energy, even though heat is being added, then the gas must be using all the heat being added to the gas to do work on the surroundings. In other words:

\[w_{done\, by\, gas} = - q_{added\, to\, gas}\label{2.1.14}\]

The work that the gas is doing on the surroundings is to push against the piston to expand the volume of the contained gas. If the coil adds heat to the gas in infinitesimal increments, then the volume of the gas will increase by infinitesimal increments as it pushes against the P_ex. However, as the volume expands, the P_gas will decrease infinitesimally. To maintain (or remain extremely close to) the mechanical equilibrium between P_gas and P_ex, the motor will need to reduce the pressure exerted by the piston. When the pressure exerted by the piston is reduced, P_gas will once again equal P_ex, and both pressures will be infinitesimally less than they were before the coil added the infinitesimal increment of heat to the gas. We thus have a process that meets the requirements for a reversible expansion. If we carry out the heating process to the extent that we change the volume of a gas by a significant amount, we can can assume that the process actually occurred by way of an infinite number of reversible expansions in which the gas pressure always equaled the external pressure. The total work for such a process can be calculated if we express P as a function of V:

\[P = \dfrac{nRT}{V}\label{2.1.15}\]

and then substitute into Equation \(\ref{2.1.12}\) to obtain

\[w = -\int \dfrac{nRT}{V} \,dV = -nRT\int \dfrac{dV}{V} = -nRT\ln \dfrac{V_f}{V_i}\label{2.1.16}\]

Because \(V_f\) is larger than \(V_i\), the work will be negative, as is expected when work is done by the system.

(The exact same result could be obtained by reducing the pressure exerted by the piston by infinitesimal amounts. After each incremental reduction in P_ex, the gas would respond by expanding doing work against the piston until its volume increased to the point at which P_gas was equal to the new, lower P_ex. The heater coil would need to respond by transferring the appropriate amount of heat into the gas to maintain a constant temperature.)

Figure \(\PageIndex {5}\) is an indicator diagram for this reversible process, starting at the high pressure, low volume state, and ending at the low pressure, high volume state.

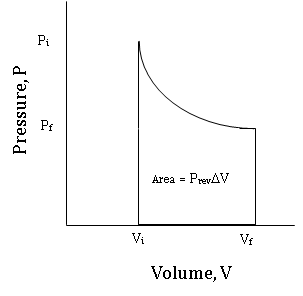
Figure \(\PageIndex {6}\) compares the indicator diagram for the reversible expansion from V_i to V_f to the indicator diagram of an irreversible expansion from V_i to V_f against a constant pressure equal to the final P_ex attained by the reversible process.

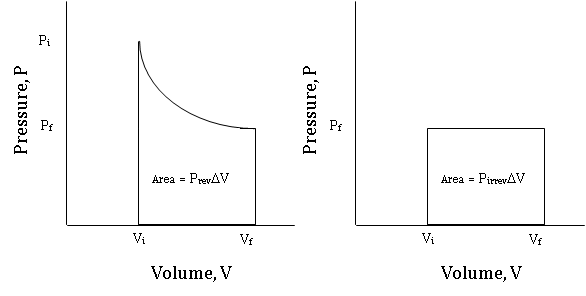
It is easy to see that the area under the curve of the reversible expansion is greater than the area under the curve of the constant pressure, irreversible expansion. This extra area represents the extra work that can be done by the system is the process is carried out reversibly rather than irreversibly. The fact that reversible processes provide maximum work will be expanded upon in Chapter 3, section A.

Note

In this example we are claiming that the heat added to the gas by the coil was never able to raise the temperature of the gas, but instead was used by the gas to do work. We are also claiming that the system was always at mechanical equilibrium, with P = P_ex, even though each infinitesimal change could happen only if P \(\ne\) P_ex. These are impossible parameters to meet, but by assuming them, we can calculate the maximum work that could be done by the process.

Example \(\PageIndex{4}\):

Suppose 3.00 moles of an perfect gas held in a 4.00 L container at 20.0 bar undergoes a reversible, isothermal expansion to a final pressure of 5.00 bar. How much work was done by the gas?

Strategy: As in Example 2.1.2, you need to calculate the temperature and final volume of the gas sample. You then use Equation \(\ref{2.1.16}\) to find the work done by the gas.

Answer: \(T = \dfrac{P_i·V_i}{nR} = \dfrac{(20.0 bar)(4.00 L)}{(3.00 moles)(0.08314 \dfrac{bar·L}{mole·K})} = 321 K\)

\(V_f = \dfrac{nRT}{P_f} = \dfrac{(3.00 moles)(0.08314 \dfrac{bar·L}{mole·K})(321 K)}{5.00 bar} = 16.0 L\)

\(w = -nRT\ln \dfrac{V_f}{V_i} = -(3.00 moles \, x \, 8.314 \dfrac{J}{mole·K} \, x \, 321 K \, x \, \ln \dfrac{16.0 L}{4.00 L} = - 1.11 x 10^4 J\)

Notice that the reversible process does about twice as much work as the one-step irreversible process!

Exercise \(\PageIndex{4}\)

Suppose 2.50 moles of an perfect gas held in a 2.00 L container at 10.0 bar undergoes an irreversible, isothermal expansion against a constant external pressure of 2.00 bar. How much work was done by the gas?

Answer: -3.22 x 10³ J

Heat Transfer

Some systems can do no work. If the system is a gas, this would mean that the container in which the gas is held has a constant volume. Because no work can be done, the only way in which the system can change internal energy is to gain or lose heat. For such a system, the first law would be

\[\Delta U = q_V\label{2.1.17}\]

where the subscript "V" indicates that the system is at constant volume.

Calorimetry

Calorimetry is the experimental measurement of heat changes. The basic premise of a calorimetry experiment is that the first law will always be followed; heat can be neither created nor destroyed:

\[q_{system} = - q_{surroundings}\label{2.1.18}\]

Constant Volume Calorimetry, also know as bomb calorimetry, is used to measure the \(q_V\) for many exothermic processes, such as combustion reactions. A bomb calorimeter structure consists of the following:

• Steel inner container ("bomb") which contains the reactants
• Water bath in which the bomb is submerged
• Thermometer
• A motorized stirrer
• Wire for ignition

All of these components are contained within the double-walled outer part of the calorimeter (Figure 1). Since the process takes place at constant volume, the reaction vessel must be constructed to withstand the high pressure resulting from the combustion process, which amounts to a confined explosion. The vessel is usually called a “bomb”, and the technique is known as bomb calorimetry.

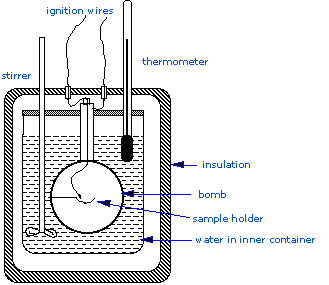
Figure 1: A simplified bomb calorimeter

In an adiabatic, constant-volume calorimeter, the entire experiment is sealed or isolated from the rest of the room so that no heat will enter or leave the calorimeter "universe". Under these conditions, the change in heat of the reaction will be equal, but opposite, to the change in heat of the surroundings, which is limited to the water and other components of the calorimeter.

\[q_{reaction} = - q_{calorimeter}\label{2.1.19}\]

The value of \(q_{calorimeter}\) actually depends on two terms

\[q_{calorimeter} = q_{water} + q_{bomb}\label{2.1.20}\]

but if the same amount of water is used for every experiment, then Equation \(\ref{2.1.19}\) is valid for all experiments.

Once the initial temperature of the calorimeter water has been measured, the heated wire inside the bomb is used to start the reaction. The temperature inside the calorimeter rises due to the conversion from chemical energy to thermal energy that occurs through the combustion reaction. To ensure complete combustion, the experiment is carried out in the presence of oxygen above atmospheric pressure. After combustion the final temperature of the calorimeter water is measured. However, the heat given off by the reaction not only heated the calorimeter water; it also heated the calorimeter apparatus, itself. Thus, it is necessary to determine the calorimeter constant, \(C\), which is the fixed amount of energy needed to raise the temperature of the calorimeter apparatus 1 kelvin.

\[C = \dfrac{q_{calorimeter}}{\Delta T}\label{2.1.21}\]

The value of C is usually determined by one of two methods. A chemical reaction with a known heat output can be carried out in the calorimeter. You know the value of \(q_{reaction}\) and thus the value of \(q_{calorimeter}\) for the known amount of water in your calorimeter. You also know the \(\Delta T\) for the reaction, so you can calculate the value of \(C\).

The second method involves adding heat to the calorimeter apparatus by means of an electrical heater. If you pass a constant electrical current (\(I\)) through a heater with a known voltage drop (\(\Delta\phi\)) for a known amount of time (\(t\)), you can calculate the heat added to the calorimeter apparatus by the fact that heat = (current)(time)(potential difference):

\[q = \Delta\phi·I·t\label{2.1.22}\]

Example \(\PageIndex{5}\):

The temperature of a calorimeter rises 6.00 K when a 12.0 V power supply is used to pass a 17.0 amp current through a heating coil for 200. seconds. What is the value of C for the calorimeter?

Strategy:

Step 1: Use Equation \(\ref{2.1.19}\) to calculate \(q_{reaction}\) (because the heater is the source of added heat). Remember that \(1\, Volt = 1 \dfrac{Joule}{Coulomb} = 1\dfrac{J}{C}\) and that \(1 \, ampere = 1 \dfrac{Coulomb}{second} = 1\dfrac {C}{s}\).

Step 2: Use Equation \(\ref{2.1.21}\) to calculate \(C\).

Answer:

Step 1: \(q_{reaction} = \Delta\phi·I·t = (12.0 \dfrac{J}{C})(17.0 \dfrac{C}{s})(200. s)(\dfrac{1 \, kJ}{1000 \, J)} = 40.8\, kJ\)

Step 2: \(C = \dfrac{40.8\, kJ}{6.00\, K} = 6.80 \dfrac{kJ}{K}\)

Exercise \(\PageIndex{5}\)

The temperature of a calorimeter rises 8.00 K when a 12.0 V power supply is used to pass a 20.0 amp current through a heating coil for 150. seconds. What is the value of C for the calorimeter?

Answer: 4.50 \(\dfrac{kJ}{K}\)

Other Calorimeters

There are many other types of calorimeters other than bomb calorimeters including isobaric calorimeters (example: a coffee cup open to the atmosphere), adiabatic flame calorimeters (a constant-pressure calorimeter used for combustion reactions), differential scanning calorimeters (DSC, a calorimeter which compares the amount of energy needed to keep the temperature of a sample and the temperature of a standard reference material the same as energy is added to both substances), and isothermal titration calorimeters (a calorimeter similar to a DSC, but which moderates the energy needed to maintain equal temperatures of a reference and a chemical reaction as precisely measured volumes of a reagent are added to the reaction mixture.)

Heat Capacity

As noted earlier, the internal energy of a system increases as the temperature of the system increases. If we are working with a pure substance that is kept at a constant volume, we can obtain both an intensive and extensive property of the substance from a plot of the internal energy versus the temperature. The slope of the tangent line to the \(U\) vs \(T\) curve at any temperature is known as the heat capacity at constant volume \(C_v\) for that substance:

\[C_V = \left( \dfrac{\partial U}{\partial T} \right)_V \label{2.1.23}\]

This is a partial derivative because the internal energy of a system will typically vary with both volume and temperature, but we are holding the volume constant and allowing only the temperature to change.

Because \(C_V\) tells us the amount of heat needed to change the temperature of a sample of a substance at constant volume, we can also say that an infinitesimal change in internal energy is equal to an infinitesimal change in temperature multiplied by the heat capacity at constant volume

\[dU = C_V \, dT\label{2.1.24}\]

If the heat capacity at constant volume of the substance does not change a great deal as the temperature changes, then the slope of the \(U\) versus \(T\) graph will be fairly constant. In this case

\[\Delta U = \int C_V \, dT \, = \, C_V·(T_2 - T_1) = C_V·\Delta T\label{2.1.25}\]

As noted in Equation \(\ref{2.1.17}\),

\[\Delta U = q_V\tag{2.1.17}\]

so that

\[q_V = C_V·\Delta T\label{2.1.26}\]

Equation \(\ref{2.1.26}\) shows us that we can experimentally determine the constant volume heat capacity of a substance fairly easily by measuring the change in temperature of a substance as heat is added to it.

The value of \(C_V\) is an extensive property because it tells us how much heat is need to change the temperature of that specific sample of the pure substance. We can determine the intensive property of this pure substance, the molar heat capacity at constant volume, \(C_{V,m}\), if we divide the experimentally obtained \(C_V\) by the number of moles of the substance used in the experiment:

\[C_{V,m} = \dfrac {C_V}{n}\label{2.1.27}\]

We can also calculate a second intensive property, the specific heat capacity, \(C_{V,s}\), which is the heat capacity per mass of sample:

\[C_{V,s} = \dfrac {C_V}{mass}\label{2.1.28}\]

Example \(\PageIndex{6}\):

When 18.9 kJ is transferred to a gas sample in a constant-volume adiabatic container with a calorimeter constant of 2.22 \(\dfrac{kJ}{K}\) , the temperature of the gas (and calorimeter) increases by 8.06 K.

A. What is the heat capacity of the sample?

B. If the sample has a mass of 0.500 kilograms, what is the specific heat capacity of the substance?

C. If the sample is krypton, what is the molar heat capacity at constant volume of krypton?

Strategy:

A. Use a modified version of Equation \(\ref{2.1.18}\),

\[q_{added} = -(q_{calorimeter} + q_{V \, gas})\label{2.1.29}\]

and substitute in Equations \(\ref{2.1.21}\) and \(\ref{2.1.26}\) to obtain

\[q_{added} = -(C_{calorimeter}\Delta T + C_{V \, gas}\Delta T)\label{2.1.30}\]

Then solve for \(C_{V\, gas}\).

B. Use Equation \(\ref{2.1.28}\) to find the specific heat capacity.

C. Determine the number of moles of krypton present and then use Equation \(\ref{2.1.27}\) to find the molar heat capacity at constant volume.

Answer:

A. \(-18,900 J = -[(2,220\dfrac{J}{K})(8.06 K) + (C_{V\, gas})(8.06 K)]\)

\(\dfrac{18,900 J - 17,893 J}{8.06 K} = C_{V\, gas}\)

\(125 \dfrac{J}{K} = C_{V\, gas}\)

B. \(C_{V,s\, gas} = \dfrac{C_{V\, gas}}{mass} = \dfrac{125 \dfrac{J}{K}}{0.500 kg} = 250. \dfrac{J}{kg·K}\)

C. \(moles Kr = \dfrac{grams Kr}{83.8 \dfrac{grams}{mole}} = \dfrac{500. grams}{83.8 \dfrac{grams}{mole}} = 5.97 moles\)

\(C_{V,m\, gas} = \dfrac{C_{V\, gas}}{moles} = \dfrac{125 \dfrac{J}{K}}{5.97 moles} = 20.9 \dfrac{J}{mole·K}\)

Exercise \(\PageIndex{6}\)

When 20.3 kJ is transferred to a 253 gram gas sample in a constant-volume adiabatic container with a calorimeter constant of 4.30 \(\dfrac{kJ}{K}\), the temperature of the gas (and calorimeter) increases by 4.50 K. What is the specific heat capacity of the substance?

Answer: \(C_{V,s} = 834 \dfrac{J}{kg·K}\)

Note

It should be noted that the temperature of a pure substance does not change during phase changes. The heat being added is breaking up the electrostatic interactions that hold the particles together. With \(\Delta T = 0\), Equation \(\ref{2.1.26}\) tells us that the \(C_V\) at phase changes must approach infinity:

\[C_V = \dfrac{q_V}{\Delta T} = \dfrac{q_V}{0}\label{2.1.31}\]

References

1. Chang, Raymond. Physical Chemistry for the Biosciences. Sausalito, CA: University Science, 2005.

• Contributors

  • Howard DeVoe, Associate Professor Emeritus, University of Maryland from Thermodynamics and Chemistry

• Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook

• Tom Neils (Grand Rapids Community College)