14.3: Kinetic vs. Thermodynamic Control of Reactions
- Page ID
- 239245
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)After completing this section, you should be able to
- explain the difference between thermodynamic and kinetic control of a chemical reaction; for example, the reaction of a conjugated diene with one equivalent of hydrogen halide.
- draw a reaction energy diagram for a reaction which can result in both a thermodynamically controlled product and a kinetically controlled product.
- explain how reaction conditions can determine the product ratio in a reaction in which there is competition between thermodynamic and kinetic control.
Make certain that you can define, and use in context, the key terms below.
- kinetic control
- thermodynamic control
Like non-conjugated dienes, conjugated dienes are subject to attack by electrophiles. In fact, conjugated dienes experience relatively greater kinetic reactivity when reacted with electrophiles than non-conjugated dienes do. The reaction mechanism is similar to other electrophilic addition reactions to alkenes (Section 7.9). During the electrophilic addition of HBr to a 1,3-butadiene, However, there are two possible outcomes once the carbocation intermediate is formed. The allyl carbocation is stabilized by resonance structures that vary in the position of the carbocation. This allows the bromide ion to add to either of these carbons resulting in the formation 1,2 and 1,4 addition products. When this reaction is run at a temperature of 0 oC or lower, the 1,2 addition product dominates. However, if the same reaction is run at 40 oC the 1,4 addition product dominates. The reaction of one equivalent of hydrogen bromide with 1,3-butadiene gives different products under different reaction conditions and is a classic example of the concept of thermodynamic versus kinetic control of a reaction.
At lower temperatures the formation of the 1,2 and 1,4 addition products are irreversible and thus do no have an equilibrium. When a reaction is irreversible the major product is determined by the relative reaction rates and not by thermodynamic stability. Of the two, the formation of the 1,2 addition product has a higher rate of reaction and forms faster making it the major product. The reaction product which formed with a higher rate of reaction is called the Kinetic Product and when the kinetic product dominates the reaction is said to be under Kinetic Control.
At higher temperatures the reaction to form both products becomes reversible and a reaction equilibrium is reached. When a reaction is reversible the major product is determined by thermodynamic stability. The 1,4 addition product is the more stable and becomes the major product under these reaction conditions. When the more stable product is called the Thermodynamic Product and when the thermodynamic product dominates the reaction is said to be under Thermodynamic Control.
The 1,4 addition product is more stable because has an internal, disubstituted double bond, and we know that as a general rule that the thermodynamic stability of an alkene increases with increasing substitution. So, when compared to the terminal, monosubstituted alkene of the 1,2 addition product, the 1,4 addition product is expected to be more stable.
A simple definition is that the kinetic product is the product that is formed faster, and the thermodynamic product is the product that is more stable. This is precisely what is happening here. The kinetic product is 3-bromobut-1-ene, and the thermodynamic product is 1-bromobut-2-ene (specifically, the trans isomer).
An explanation for the temperature influence is shown in the following energy diagram for the addition of HBr to 1,3-butadiene. The initial step in which a proton bonds to carbon #1 is the rate determining step, as indicated by the large activation energy (light gray arrow). The second faster step is the product determining step, and there are two reaction paths (colored blue for 1,2-addition and magenta for 1,4-addition).
At elevated temperatures, the products are more likely to have enough energy to overcome the reverse activation barriers to regenerate the carbocation intermediate. Under these conditions, this step of the mechanism will be reversible and an equilibrium will be established. Since the system is no longer limited by temperature, the system will minimize its Gibbs free energy, which is the thermodynamic criterion for chemical equilibrium. This places the reaction under thermodynamic control and the most thermodynamically stable molecule, the 1,4 addition product, will be predominantly formed.
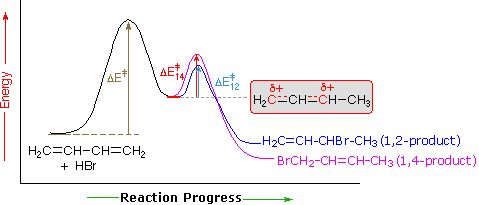
If the reaction temperature is kept sufficiently low, the products will probably not have enough energy to overcome the reverse activation barrier to regenerate the carbocation intermediate making this step of the mechanism effectively irreversible. This reaction is under kinetic control meaning the product which forms faster, the kinetic product, will predominate.
Of the two reaction pathways, the 1,2-addition has a smaller activation energy and would be expected to have a higher reaction rate than the 1,4-addition. The high reaction rate for 1,2-addition can also be attributed to the formation of an ion pair during the reaction mechanism. This means that, after a double bond is protonated, the halide counterion remains in close proximity to the carbocation generated. Immediately following dissociation of , the chloride ion is going to be much closer to than it is to , and therefore attack at is much faster. This ion pair mechanism is a pre-exponential constant effects that is attributed to the proximity and frequency of collision rather than a activation barrier effect.
Exercise \(\PageIndex{1}\)
1) Why is the 1,4-addition product the thermodynamically more stable product?
2) Addition of 1 equivalent of bromine to 2,4-hexadiene at 0 degrees C gives 4,5-dibromo-2-hexene plus an isomer. What is the structure of that isomer?
3) The kinetically controlled product in the below reaction is:

4) For the reaction above, which product is the result of 1,4-addition?

5) What would be the major product of the addition of HBr to 2,3-dimethyl-1,3-cyclohexadiene under thermodynamic conditions?
6) Consider the reaction with 1,3-buta-diene reacting with HCl. Propose a mechanism for the reaction. Also, Predict why the 1,4 adduct is the major product in this reaction compared to the 1,2.
- Answer
-
1) The 1,4- product is more thermodynamically stable because there are two alkyl groups on each side of the double bond and more substituted alkenes are more stable.
2) 2,5-Dibromo-3-hexene
3) 3-Chloro-1-butene
4) 1-Chloro-2-butene
5)

6)
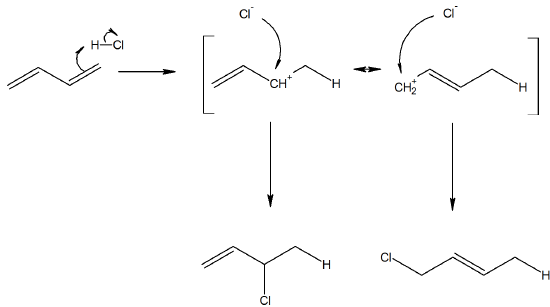
Even though the cation would prefer to be in a secondary position in the transition state, the final product is less stable with a terminal alkene. Therefore the major product will be the 1,4 adduct.
Contributors and Attributions
- Orthocresol (@chemistry StackExchange)
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
- Natasha Singh

