3.6: Conformations of Ethane
- Page ID
- 239096
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objectives
After completing this section, you should be able to
- explain the concept of free rotation about a carbon-carbon single bond.
- explain the difference between conformational isomerism and structural isomerism.
- draw the conformers of ethane using both sawhorse representation and Newman projection.
- sketch a graph of energy versus bond rotation for ethane, and discuss the graph in terms of torsional strain.
Key Terms
Make certain that you can define, and use in context, the key terms below.
- conformation (conformer, conformational isomer)
- dihedral angle
- eclipsed conformation
- Newman projection
- staggered conformation
- strain energy
- torsional strain (eclipsing strain)
Study Notes
You should be prepared to sketch various conformers using both sawhorse representations and Newman projections. Each method has its own advantages, depending upon the circumstances. Notice that when drawing the Newman projection of the eclipsed conformation of ethane, you cannot clearly draw the rear hydrogens exactly behind the front ones. This is an inherent limitation associated with representing a 3-D structure in two dimensions.
Conformational isomerism involves rotation about sigma bonds, and does not involve any differences in the connectivity of the atoms or geometry of bonding. Two or more structures that are categorized as conformational isomers, or conformers, are really just two of the exact same molecule that differ only in rotation of one or more sigma bonds.
Ethane Conformations
Although there are seven sigma bonds in the ethane molecule, rotation about the six carbon-hydrogen bonds does not result in any change in the shape of the molecule because the hydrogen atoms are essentially spherical. Rotation about the carbon-carbon bond, however, results in many different possible molecular conformations.

In order to better visualize these different conformations, it is convenient to use a drawing convention called the Newman projection. In a Newman projection, we look lengthwise down a specific bond of interest – in this case, the carbon-carbon bond in ethane. We depict the ‘front’ atom as a dot, and the ‘back’ atom as a larger circle.

The six carbon-hydrogen bonds are shown as solid lines protruding from the two carbons at 120°angles, which is what the actual tetrahedral geometry looks like when viewed from this perspective and flattened into two dimensions.
Interactive Element
A 3D Model of Staggered Ethane.
The lowest energy conformation of ethane, shown in the figure above, is called the ‘staggered’ conformation. In the staggered conformation, all of the C-H bonds on the front carbon are positioned at an angle of 60° relative to the C-H bonds on the back carbon. This angle between a sigma bond on the front carbon compared to a sigma bond on the back carbon is called the dihedral angle. In this conformation, the distance between the bonds (and the electrons in them) is maximized. Maximizing the distance between the electrons decreases the electrostatic repulsion between the electrons and results in a more stable structure.
If we now rotate the front CH3 group 60° clockwise, the molecule is in the highest energy ‘eclipsed' conformation, and the hydrogens on the front carbon are as close as possible to the hydrogens on the back carbon.
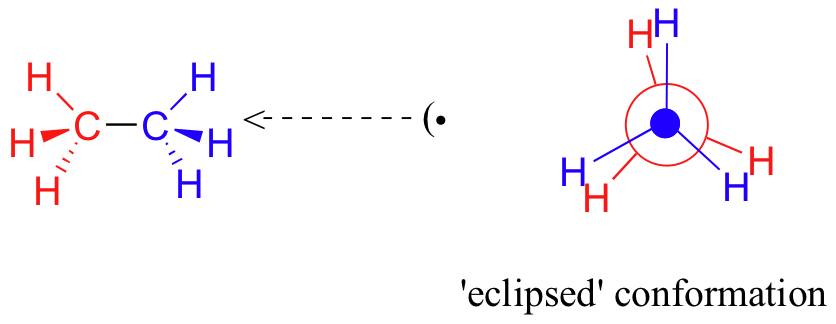
This is the highest energy conformation because of unfavorable electrostatic repulsion between the electrons in the front and back C-H bonds. Each hydrogen-hydrogen eclipsing interaction creates 1.0 kcal/mol (4.0 kJ/mol) of torsional strain. Because there are three such interactions, the energy of the eclipsed conformation is approximately 3 kcal/mol (12 kJ/mol) higher than that of the staggered conformation. Torsional strain (or eclipsing strain) is the name give to the energy difference caused by the increased electrostatic repulsion of eclipsing bonds.
Another 60° rotation returns the molecule to a second eclipsed conformation. This process can be continued all around the 360° circle, with three possible eclipsed conformations and three staggered conformations, in addition to an infinite number of variations in between. We will focus on the staggered and eclipsed conformers since they are, respectively, the lowest and highest energy conformers.
Unhindered (Free) Rotations Do Not Exist in Ethane
The carbon-carbon bond is not completely free to rotate – the 3 kcal/mol torsional strain in ethane creates a barrier to rotation that must be overcome for the bond to rotate from one staggered conformation to another. This rotational barrier is not large enough to prevent rotation except at extremely cold temperatures. So at normal temperatures, the carbon-carbon bond is constantly rotating. However, at any given moment the molecule is more likely to be in a staggered conformation - one of the rotational ‘energy valleys’ - than in any other conformer. The potential energy associated with the various conformations of ethane varies with the dihedral angle of the bonds, as shown in figure 3.6.1.
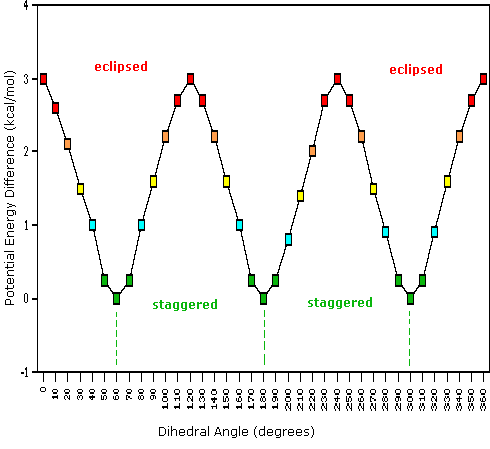
Figure 3.6.1: The potential energy associated with the various conformations of ethane varies with the dihedral angle of the bonds. Valleys in the graph represent the low energy staggered conformers, while peaks represent the higher energy eclipsed conformers.
Although the conformers of ethane are in rapid equilibrium with each other, the 3 kcal/mol energy difference leads to a substantial preponderance of staggered conformers (> 99.9%) at any given time. The animation below illustrates the relationship between ethane's potential energy and its dihedral angle
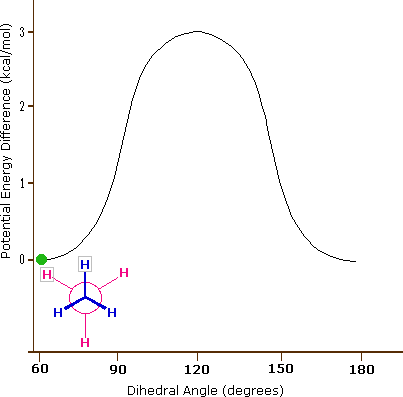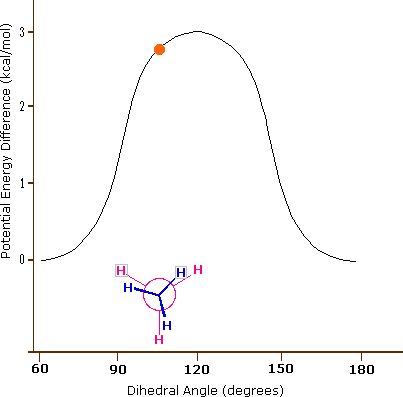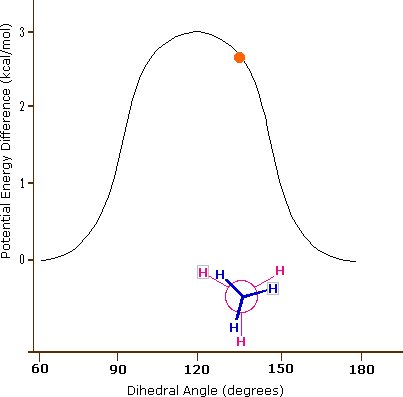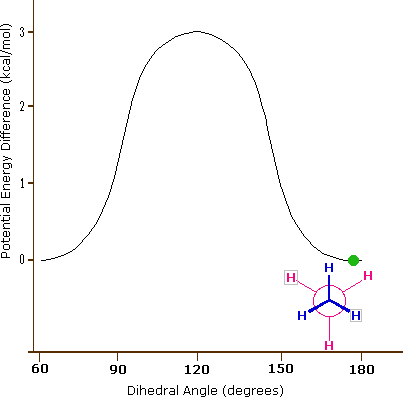
Figure 3.6.2: Animation of potential energy vs. dihedral angle in ethane
Exercises
1) What is the most stable rotational conformation of ethane and explain why it is preferred over the other conformation?
Solutions
1) Staggered, as there is less repulsion between the hydrogen atoms.
Contributors and Attributions
William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)

