Kinetic Theory of Gases
- Page ID
- 1520
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The kinetic theory of gases (also known as kinetic-molecular theory) explains the behavior of a hypothetical ideal gas. According to this theory, gases are made up of tiny particles in random, straight line motion. They move rapidly and continuously and make collisions with each other and the walls. This was the first theory to describe gas pressure in terms of collisions with the walls of the container, rather than from static forces that push the molecules apart. Kinetic theory also explains how the different sizes of the particles in a gas can give them different, individual speeds.
Postulates
Kinetic theory makes many assumptions in order to explain the reasons gases act the way they do. According to kinetic theory:
- Gases consist of particles in constant, random motion. They continue in a straight line until they collide with something—usually each other or the walls of their container.
- Particles are point masses with no volume. The particles are so small compared to the space between them, that we do not consider their size in ideal gases.
- No molecular forces are at work. This means that there is no attraction or repulsion between the particles.
- Gas pressure is due to the molecules colliding with the walls of the container. All of these collisions are perfectly elastic, meaning that there is no change in energy of either the particles or the wall upon collision. No energy is lost or gained from collisions.
- The time it takes to collide is negligible compared with the time between collisions.
- The kinetic energy of a gas is a measure of its Kelvin temperature. Individual gas molecules have different speeds, but the temperature and kinetic energy of the gas refer to the average of these speeds.
- The average kinetic energy of a gas particle is directly proportional to the temperature. An increase in temperature increases the speed in which the gas molecules move.
- All gases at a given temperature have the same average kinetic energy.
- Lighter gas molecules move faster than heavier molecules.
Thermal Energy
Keep in mind that the temperature of a gas is actually a measure of its average kinetic energy, and kinetic energy of a particle is related to its velocity according to the following equation:
\[ KE= \frac{1}{2} mv^2\]
where KE represents kinetic energy of a particle, m equals mass, and v2 is the square of its velocity. As velocity increases so does kinetic energy. Of course the inverse is also true, that as kinetic energy increases so does velocity. You can see from this relationship how a molecule with a higher temperature will be moving faster. The temperature of the system is the average kinetic energy of its particles. Thermal energy is the total kinetic energy of all the particles in a system. Temperature, thermal energy, and the speed of a molecule are all directly related.
The "ABC Gas Laws"
Avogadro's Law
Avogadro’s law states that the volume of a gas is directly related to the number of moles of atoms contained in the gas. The equation for Avogadro's law is
\[V/n= k\]
where \(V\) is the volume of the container, \(n\) is the amount of gas as measured by the moles of atoms, and \(k\) is a constant. Say you have a given amount of particles in a box. If you want to add more particles, but you do not want to increase the pressure, you must make the container larger.
Boyle's Law
Boyle’s law states that for the pressure and volume of a gas, when one value increases the other decreases, as long as temperature and number of moles remain constant. Boyle's law is summarized by the equation
\[PV=k\]
where \(P\) is the pressure of the molecules on the container, \(V\) is the volume of the container, and \(k\) is a constant.
The value of \(k\) always stays the same so that P and V vary appropriately. For example, if pressure increases, k must remains constant and thus volume will decrease. This is consistent with the predictions of Boyle's law.
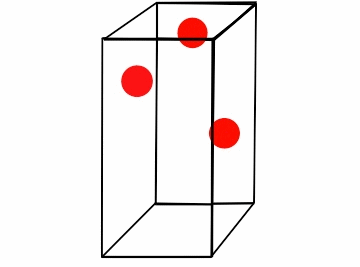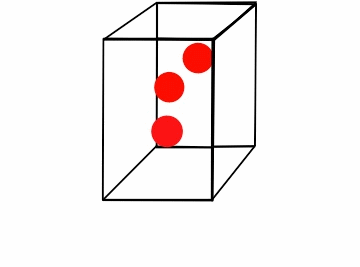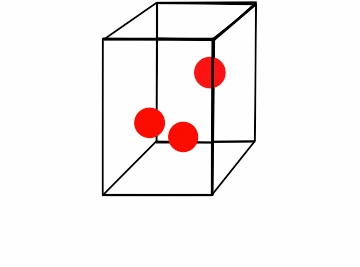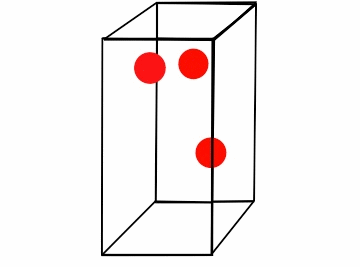
Figure \(\PageIndex{1}\): Boyle's law for a box of varying volume.*
Consider the box full of moving gas molecules (Figure \(\PageIndex{1}\)). The particles have the same energy (temperature) throughout. As the box gets smaller, they have a smaller distance to travel before they collide with the walls, and thus the time between collisions gets increasingly smaller. In a given amount of time the partials hit the walls more, which results in a greater amount of pressure. The amount of moles is clearly constant, as we are not adding or subtracting particles from the box. Another way of looking at this is that as the pressure increases, it drives the particles together. These compacted particles now occupy less volume. In order to compare a gas where either pressure or volume vary, we can combine the equations P1V1= k and P2V2= k. Because k is constant for both values of pressure and volume,
\[P_1V_1=P_2V_2\]
This equation for Boyle's law is helpful when solving problems.
Charles' Law
Charles’ law states that the values for temperature and volume of a gas are directly related. The equation for Charles' law is
\[\dfrac{V}{T}=k\]
where \(V\) is the volume of the container, \(T\) is the temperature of the system in Kelvin, and \(k\) is the constant.
For changes in volume and temperature, \(k\) remains the same.
According to Charles' law, gases will expand when heated. The temperature of a gas is really a measure of the average kinetic energy of the particles. As the kinetic energy increases, the particles will move faster and want to make more collisions with the container. However, remember that in order for the law to apply, the pressure must remain constant. The only way to do this is by increasing the volume. This idea is illustrated by the comparing the particles in the small and large boxes.
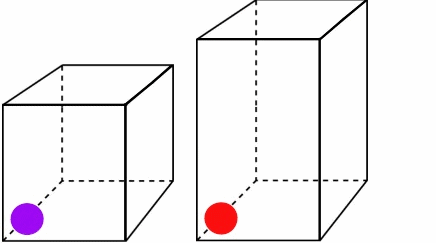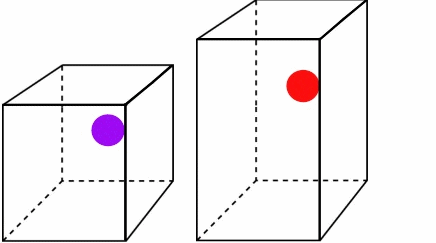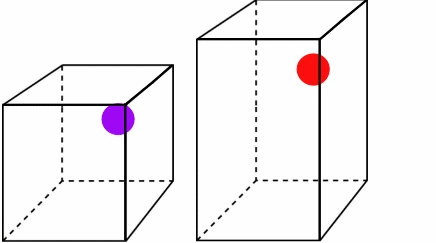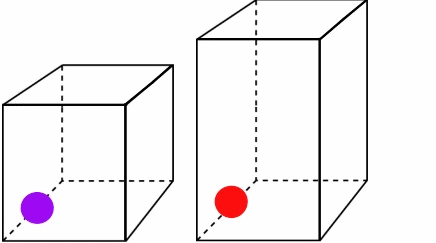
Figure \(\PageIndex{2}\):The higher temperature and speed of the red ball means it covers more volume in a given time.*
Both particles leave at and return at the same time, but since the red ball travels a longer distance, it must be moving faster and have more energy. You can see that as the temperature and kinetic energy increase, so does the volume. Also note how the pressure remains constant. Both boxes experience the same number of collisions in a given amount of time. For Charles' Law, you can write the combined equation
\[V_1/T_1= V_2/T_2\]
The Pressure Law (Gay-Lussac's Law)
The pressure law states that the values for temperature and pressure of a gas are directly related. As the temperature of a gas increases, so will the average speed and kinetic energy of the particles. This relationship is expressed in the following equation,
\[\dfrac{P}{T}= k\]
where \(P\) is the pressure of the particles on the container, \(T\) is the temperature in Kelvin, and \(k\) is a constant. At constant volume, this results in more collisions and thereby greater pressure the container. Because the value of k is the same for differing values of pressure and temperature, the pressure law can be written
\[\dfrac{P_1}{T_1} = \dfrac{P_2}{T_2}\]
Graham’s Law of Effusion
Effusion is the process where gas molecules escape from an evacuated container though a small hole into a vacuum. It is assumed that while a molecule is exiting, there are no collisions on that molecule.
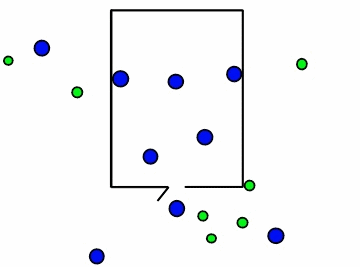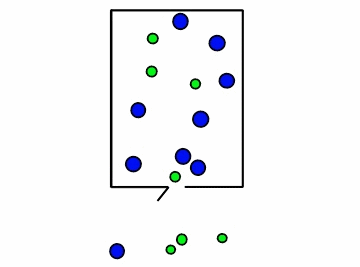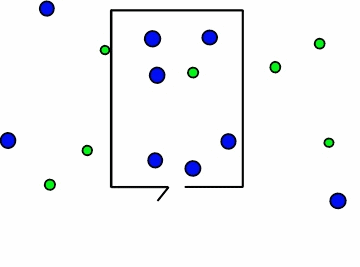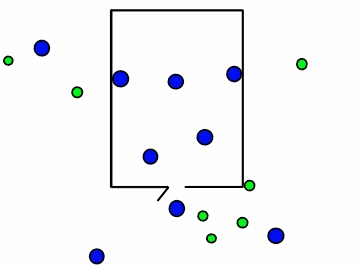
Figure \(\PageIndex{4}\): Effusion of gas molecules from an evacuated container.*
Note how the lighter molecules are the first to exit because they have a faster speed. You can see in Figure \(\PageIndex{4}\) above, the smaller green molecules exit at a faster rate. This is where Graham's law of effusion comes in. It tells us the rate at which the molecules of a certain gas exit the container, or effuse. Thomas Graham, a Scottish chemist, discovered that lightweight gases diffuse at a much faster rate than heavy gases. Graham's law of effusion shows the relationship between effusion rates and molar mass.
\[ \text{rate of diffusion} \propto \dfrac{1}{\sqrt{\text{molar mass}}} \]
To see how Graham's law of effusion is derived from kinetic theory, consider the equation for the kinetic energy of a gas (ignoring rotation).
\[ KE= \dfrac{1}{2} mv^2 \]
Because temperature is a measure of the average kinetic energy of a gas, two gases at the same temperature will also have the same kinetic energy. Thus,
\[ \dfrac{1}{2} m_1v_1^2= \dfrac{1}{2} m_2v_2^2 \]
Simplify by multiplying both sides by two,
\[ m_1v_1^2= m_2v_2^2 \]
By rearranging terms, we get
\[ \dfrac{v_1^2}{v_2^2}= \dfrac{m_2}{m_1} \]
Taking the square root of both sides gives the equation,
\[ \dfrac{v_1}{v_2}= \sqrt {\dfrac{m_2}{m_1}} \]
where \(v_1\) is the average velocity of the molecules in gas 1, \(v_2\) is the average velocity of the molecules in gas 2, and \(m_1\) and \(m_2\) are their respective molar masses. According to Graham's law, the molecular speed is directly proportional to the rate of effusion. You can imagine that molecules that are moving around faster will effuse more quickly, and similarity molecules with smaller velocities effuse slower. Because this is true, we can substitute the rates of effusion into the equation below. This yields Graham's law of effusion.
\[ \dfrac{rate_1}{rate_2}= \sqrt {\dfrac{M_2}{M_1}} \label{graham}\]
Equation \ref{graham} allows us to compare the rates of effusion for two different gases under the same conditions of temperature and pressure. It is important to note that when solving problems for effusion, the gases must contain equal moles of atoms. You can still solve the equation if they are not in equal amounts, but you must account for this. For example, if gas A and gas B both diffuse in the same amount of time, but gas A contains 2 moles and gas B contains 1 mole, then the rate of effusion for gas A is twice as much.
For example, consider the effusion of hydrogen and oxygen gases. Since both gases are diatomic at room temperature, the molar mass of hydrogen is about 2.0 grams/mol and the molar mass of oxygen is about 32 grams/mol. Inserting these values into Equation \ref{graham}
\[\dfrac{\text{rate of } \ce{H2}} {\text{rate of } \ce{O2}} = \sqrt{ \dfrac{32}{2}} = \sqrt{16} = 4\]
results in that hydrogen gas will diffuse four times faster than oxygen gas.
Diffusion
Diffusion is a process that involves mass transfer like effusion, but is more.complicated since the nature of the intermolecular interactions must be addressed. When you open a bottle of perfume, it can very quickly be smelled on the other side of the room. This is because as the scent particles drift out of the bottle, gas molecules in the air collide with the particles and gradually distribute them throughout the air. Diffusion of a gas is the process where particles of one gas are spread throughout another gas by molecular motion.

Figure \(\PageIndex{3}\): Diffusion of gas molecules into a less populated region.
As with effusion, not all gases diffuse at the same rate. Figure \(\PageIndex{3}\) above shows the perfume as being composed of all the same molecules. In reality the perfume would be composed of many different types of molecules: some larger, more dense molecules and other smaller, lighter molecules.
Root Mean Square (RMS) Speed
We know how to determine the average kinetic energy of a gas, but how does this relate to the average speed of the particles? We know that in a gas individual molecules have different speeds. Collisions between these molecules can change individual molecular speeds, but this does not affect the overall average speed of the system. As we have seen demonstrated through effusion, lighter gas molecules will generally move faster than heavier gases at the same temperature. But how do you determine the average speed, or velocity, of individual gas molecules at a certain temperature?
One approach would be to mathematically average the speed of the particles. Let's say we have a gas that contains only three molecules. Their relative speeds are 2 m/s, 3 m/s, and 4 m/s. The mean speed is the average of the molecular speeds of the particles of a gas:
\[ \dfrac{2+3+4}{3}= \dfrac{9}{3}= 3 \nonumber\]
The RMS speed is the average of the the squares of the molecular speeds. The RMS speed of our gas is:
\[ \sqrt{\dfrac{2^2+3^2+4^2}{3}}= \sqrt{\dfrac{29}{3}}= 3.11 \nonumber\]
However, seeing as there are almost always more than three molecules in a gas, and it would be nearly impossible to know all their speeds, this method is highly impractical.
There is another way of calculate average speed, as defined by the kinetic theory of gases.
where \(u_{rms} \) is the root mean square (RMS) speed, \(M_x\) is the molar mass of the gas, T is the absolute temperature in Kelvin, and R is the universal gas constant, which is also featured in the ideal gas law and the Nernst equation. Its value is
R= 8.314472 J/Kmol
\[ \dfrac{rate_1}{rate_2}= \dfrac{u_{rms,1}}{u_{rms,2}} = \sqrt{\dfrac{M_2}{M_1}} \]
Real Gases
Kinetic theory assumes that all gases behave ideally; however, we know that this is not the case. Obviously real gas particles do occupy space and attract each other. These properties become apparent at low temperatures or high pressures. Usually the particles have enough kinetic energy that they whiz by each other without being affected by the push or pull of neighboring molecules. However, at low temperatures the molecules have very little kinetic energy and move around much slower, so there is time for static forces to take hold. At very high pressures, the molecules of a gas become so tightly packed that their volume is significant compared to the overall volume. Also note that before a gas ever reaches absolute zero, it will condense to a liquid.
Problems
Q1
How much kinetic energy is possessed by a mole of helium atoms all moving at 30.0 m/s?
- Answer
-
This is a simple application of the definition of translational kinetic energy
\[KE= \frac{1}{2}mv^2 \nonumber\]
Note that in molecules (i.e., multiple atoms), there may be rotational and vibrational energy too. The velocity \(v\) is given in the problem and by looking at the periodic table, we see that the molar mass of helium is 4.0026 g/mol.
\[\begin{align*} KE (\text{per mole of helium}) &= \dfrac{1}{2} ( 4.0026 \;\cancel{g}) \left( \dfrac{1\; kg}{1,000 \; \cancel{g}} \right) (30 \;m/s)^2 \\[5pt] &= 1.80 \, kg \, m^2/s^2 = 1.8\; J \end{align*}\]
Q2
You are throwing a birthday party and decide to fill the room with helium balloons. You also want to have a few larger balloons to put at the door. The smaller balloons are filled occupy 0.240 m3 when the pressure inside them is 0.038 atm and the temperature of the room is 70° F. What pressure should you fill the larger balloons to so that they occupy 0.400 m3?
- Answer
-
a. First figure out which equation to use. The temperature of the room is assumed to be held constant, so it is extraneous information. Since you are dealing with volume and pressure, you would use Boyle's Law.
b. Organize the data.
P1= .038 atm, V1= .240 m3
P2=?, V2=.400 m3
c. Plug into the equation and solve.
P1V1=P2V2
(.038 atm)(.240 m3) = P2(.400 m3)
.00912 = .400 P2 (units cancel out so that pressure will be in atm)
P2 = 0.0228 atm
Q3
What is the rms velocity of an ensemble of neon atoms at 80° F.
- Answer
-
Convert Fahrenheit to Celsius
°C = (°F- 32)/1.8
= (80 -32)/1.8
= 48/1.8
= 26.6
Convert Celsius to Kelvin.
K = °C + 273.15
= 26.6 + 273.15
= 299.75 K
Plug known information into the equation for RMS speed and solve.
\[ \begin{align*} u_{rms} &= {\sqrt{\dfrac{3RT}{M_x}}} \\[5pt] &= {\sqrt{\dfrac{3(8.314472)(299.75)}{20.1797}}} \\[5pt] &= {19.2\; m/s} \end{align*}\]
References
- Biddle, Verne and Parker, Gregory. Chemistry Precision and Design. Pensacola: Pensacola Christian College. 2000.
- Egolf, Terrance R. and Shumate, Linda. Physics for Christian Schools. Greenville: BJU Publishers. 2004.
- Giancoli, Douglas C. Physics for Scientists and Engineers, 3rd Edition. Prentice Hall. 2000.
- "Gases: Graham's Laws of Diffusion and Effusion." Texas A&M University, Department of Chemistry.
- "Kinetic-Molecular Theory." University of Florida.
- Petrucci, Ralph H. General Chemistry: Principles & Modern Application, 9th Edition. New Jersey: Pearson Prentice Hall. 2007.
- Roscoe, Henry Enfield and Schorlemmer, Carl. "The Kinetic Theory of Gases." A Treatise On Chemistry. 1874.
- "Kinetic Theory of Gases." Gale Science in Context. 2008.
Contributors
- Caitlin Claunch (UCD), All animations are the original work of Caitlin Claunch.

