2.1: Octets

Charge

Up to now the charge has been added to the cation or anion without explanation. Still the convention for showing charge is straightforward. When aluminum, Al, loses 3 electrons its cation is show as Al³⁺. The 3 represents the number of electrons lost and the + indicates there is an excess of positive charge. Similarly, when oxygen, O, gains 2 electrons the anion is O^2–. The 2 represents the 2 gained electrons and the – is for the negative charge the oxygen gained.

Valence Electrons and Octets

The number of valence electrons, those electrons in the outermost energy level, determines the number of electrons an element will gain or lose. Since the families have the same pattern of outer electrons, the number of valence electrons is the same in each family.

The table above is a result of atoms losing and gaining electrons to form stable noble gas electron configurations. When an element loses electrons it commonly does so until all valence electrons are gone; thus, magnesium with 2 valence electrons will react to become Mg²⁺, magnesium cation by losing the 2 valence electrons. Likewise, when an element gains electrons, it will gain only enough electrons to fill the outer shell s and p-orbitals; such as, nitrogen with 5 valence electrons will gain 3 electrons to become N^3–, nitrogen anion, so that there are 8 electrons in the outer shell. The full outer shell of 8 electrons is is called an octet, and ions are said to be stable when they have an octet. Here are two more examples:

• K = [Ne]3s¹ ➔ (lose 1e – ) ➔ [Ne] = 1s²2s²2p⁶ = K¹⁺
• S = [Ne]3s²3p⁴ ➔ (gain 2e – ) ➔ [Ne]3s²3p⁶ = S^2– .

Noble gases do not react because they already have full shells, ns²np⁶. The energy change when electrons are added or removed is too large because the effective nuclear charge is too high for an electron to be removed easily and because adding electrons would require using a new shell which is not favorable. For nonmetals in the second period that lose electrons, the number of electrons lost will result in the noble gas electron configuration of helium 1s², so only two valence electrons are in the outer shell not an octet. Hydrogen usually loses one electron to become a single proton in the nucleus without any electrons in the electron cloud, H⁺; however, it very occasionally gains one electron to become H^– with an electron configuration similar to helium.

Lewis Structures

To show the movement of electrons in a reaction, Gilbert Lewis introduced method of writing atoms and their valence electrons using chemical symbols and dots for electrons. Lewis dot diagrams, also called Lewis structures, electron dot structures, electron dot diagrams, etc., simply show the valence electrons about the chemical symbol of an element placed on the top and bottom and on the left and right.

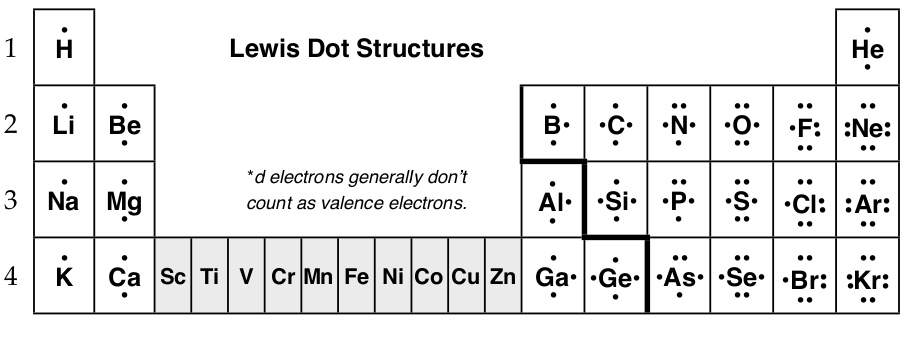
Forming Ionic Compounds

To form an ionic compound, elements must transfer electrons from one another. So if a metal and nonmetal react, then the metal will lose electrons and the nonmetal will gain electrons to make a cation and an anion. By convention the cation, usually a metal, is written before the anion. This is particularly important for writing the chemical formula of ionic compounds.

Balancing the Electrons Transferred

When electrons are transferred, the number of electrons lost and gained must be equal. To do this more atoms are added to provide a balanced number of valence electrons. For the first example below, beryllium, Be, needs to lose both outer electrons, but chlorine, Cl, only needs one. To balance the transfer of electrons needed for the atoms to reach a stable noble gas electron configuration another chlorine is added. The other examples demonstrate the balanced transfer of electrons. Here are some examples using electron dot diagrams:

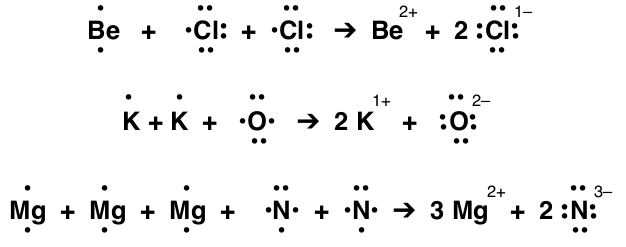
In each of these reactions the number of valence electrons lost from each metallic element must have a place to be gained by the nonmetal element. The total number of electrons lost then gained is the least common multiple of the number of valence electrons (or you can just keep track of the electrons and add elements and valence electrons until the number of electrons lost equals the number of electrons gained).

For example, Identify the number and type of ions formed in a reaction of calcium and carbon.

• Step 1: Determine the number of valence electrons for each element and whether the element loses or gains electrons. Calcium has 2 valence electrons and is a metal so it will give up two electrons. Carbon is the nonmetal and with 4 valence electrons it will gain 4 electrons (carbon gains and loses electrons depending on what the other element does, in this case calcium wants to give electrons so carbon will gain electrons).
• Step 2: Determine how many extra elements need to be added so the number of valence electrons gained equals the number lost. Carbon needs more than 2 electrons from calcium so add another calcium. Two calciums will have 4 valence electrons to lose which equals the 4 valence electrons one carbon gains.
• Step 3: Show the reaction:

Electrostatic Attractions

When ions are created they can usually dissolve in water (we will discuss solubility in another unit), or will form a solid by sticking together. The opposite charges of cations and anions will force the ions to attract. Electrostatic attraction is the name of the strong bonding force holding the cations and anions together in an ionic compound.

Crystal Lattice

There are, of course, a multitude of cations and anions present in any reaction. So each cation can attract several anions and each anion can attract several cations. The result is a repeating and organized arrangement of cations and anions called a crystal lattice. A crystal lattice is a very stable bonding for ions and a lattice bonding energy is associated with the repeated arrangement of cations and ions.

The crystal lattice of sodium chloride. Small sodium cations and larger chlorine anions in a repeating pattern held together by electrostatic attractions.

Contributors

• Kenneth Pringle and Curriki. This content is licensed under a Creative Commons Attribution Share-Alike 3.0 License.