3.3 Electrolysis of Water
- Page ID
- 32282
Our second example of electrolysis and electrolytic cells involves the breakdown of water. We will find a situation very similar to the electrolysis of molten \(\ce{NaCl}\).
The following equation represents the breaking apart of \(\ce{H2O(l)}\):
\(\ce{2H2O(l) -> 2H2(g) + O2(g)}\)
It may be more difficult to predict the half-reactions involved, but they are:
| E° | |||
| reduction | \(\ce{2H2O(l) + 2e- -> H2(g) + {2OH^{-}(g)}}\) | -0.83 V | |
| oxidation | \(\ce{2H2O(l) -> O2(g) + 4H+(aq) + 4e^{-}}\) | -1.23V | |
| net voltage required | - 2.06V | ||
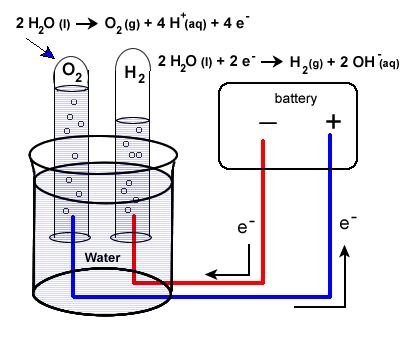
The set-up will be very similar to our last example with some minor differences. Water does not carry a charge well, so an electrolyte is added to the water. Vinegar, a weak acid (acetic acid) may be used. To collect the hydrogen and oxygen gases produced, inverted test tubes are often added, as shown in our diagram below.
Again, take special care to trace the path of the electrons. Unless electrons make a complete circuit, a reaction will not occur.
- Electrons are "produced" in the battery at the anode, the site of oxidation.
- The electrons leave the electrochemical cell through the external circuit.
- These negative electrons create a negative electrode in the electrolytic cell which causes the reduction of water.
Note that the area around this electrode will become basic as OH- ions are produced.
\(\ce{2H2O(l) + 2e- -> H2(g) + {2OH^{-}(g)}}\)
- Meanwhile the the positive electrode water will undergo oxidation:
| \(\ce{2H2O(l) -> O2(g) + 4H+(aq) + 4e^{-}}\) |
- Electrons produced during this oxidation process will return to the electrochemical cell.
 |
A note about the balanced equation for the electrolysis of water:
You may notice from the half reactions that adding up the equations doesn't initially give us our net equation of
\(\ce{2H2O(l) -> 2H2(g) + O2(g)}\)
Once you balance for electrons (multiply the reduction equation by 2) you'll find the equations actually add up to :
\(\ce{6H2O(l) -> 2H2(g) + O2(g) + 4H+(aq) + {4OH^{-}(g)}}\)
The hydrogen and hydroxide ions will combine to form 4 moles of \(\ce{2H2O(l)}\). Finding our net amount of \(\ce{2H2O(l)}\) involved gives us our final equation:
\(\ce{2H2O(l) -> 2H2(g) + O2(g)}\)

