10.E: Spectroscopic Methods (Exercises)
- Page ID
- 5616
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)1. Provide the missing information in the following table.
|
wavelength (m) |
frequency (s–1) |
wavenumber (cm–1) |
energy (J) |
|
4.50 × 10–9 |
|||
|
1.33 × 1015 |
|||
|
3215 |
|||
|
7.20 × 10–19 |
2. Provide the missing information in the following table.
|
|
|
|
molar absorptivity (M–1 cm–1) |
pathlength (cm) |
|
1.40×10–4 |
1120 |
1.00 |
||
|
0.563 |
750 |
1.00 |
||
|
2.56×10–4 |
0.225 |
440 |
||
|
1.55×10–3 |
0.167 |
5.00 |
||
|
33.3 |
565 |
1.00 |
||
|
4.35×10–3 |
21.2 |
1550 |
||
|
1.20×10–4 |
81.3 |
10.00 |
3. A solution’s transmittance is 35.0%. What is the transmittance if you dilute 25.0 mL of the solution to 50.0 mL?
4. A solution’s transmittance is 85.0% when measured in a cell with a pathlength of 1.00 cm. What is the %T if you increase the pathlength to 10.00 cm?
5. The accuracy of a spectrophotometer can be evaluated by preparing a solution of 60.06 ppm K2Cr2O7 in 0.0050 M H2SO4, and measuring its absorbance at a wavelength of 350 nm in a cell with a pathlength of 1.00 cm. The absorbance should be 0.640. What is the molar absorptivity of K2Cr2O7 at this wavelength?
6. A chemical deviation to Beer’s law may occur if the concentration of an absorbing species is affected by the position of an equilibrium reaction. Consider a weak acid, HA, for which Ka is 2 × 10–5. Construct Beer’s law calibration curves of absorbance versus the total concentration of weak acid (Ctotal = [HA] + [A−]), using values for Ctotal of 1 × 10–5, 3 × 10–5, 5 × 10–5, 9 × 10–5, 11 × 10–5, and 13 × 10–5 M for the following sets of conditions:
(a) εHA = εA– = 2000 M–1 cm–1; unbuffered solution.
(b) εHA = 2000 M–1 cm–1 and εA– = 500 M–1 cm–1; unbuffered solution.
(c) εHA = 2000 M–1 cm–1 and εA– = 500 M–1 cm–1; solution is buffered to a pH of 4.5.
Assume a constant pathlength of 1.00 cm for all samples.
7. One instrumental limitation to Beer’s law is the effect of polychromatic radiation. Consider a line source that emits radiation at two wavelengths, λ′ and λ″. When treated separately, the absorbances at these wavelengths, A′ and A″, are
\[A′ = −\log\dfrac{P_\ce{T}′}{P_0′} = ε′\,bC\]
\[A′′ = −\log\dfrac{P_\ce{T}′′}{P_0′′} = ε′′\,bC\]
If both wavelengths are measured simultaneously the absorbance is
\[A = −\log\dfrac{(P_\ce{T}′ + P_\ce{T}′′)}{(P_0′ + P_0′′)}\]
(a) Show that if the molar absorptivity at λ′ and λ″ are the same (ε′ = ε″ = ε), the absorbance is equivalent to
\[A = εbC\]
(b) Construct Beer’s law calibration curves over the concentration range of zero to 1 × 10–4 M using ε′ = 1000 and ε″ = 1000, and ε′ = 1000 and ε″ = 100. Assume a value of 1.00 cm for the pathlength. Explain the difference between the two curves.
8. A second instrumental limitation to Beer’s law is stray radiation. The following data were obtained using a cell with a pathlength of 1.00 cm when stray light is insignificant (Pstray = 0).
|
[analyte] (mM) |
absorbance |
|
0.00 |
0.00 |
|
2.00 |
0.40 |
|
4.00 |
0.80 |
|
6.00 |
1.20 |
|
8.00 |
1.60 |
|
10.00 |
2.00 |
Calculate the absorbance of each solution when Pstray is 5% of P0, and plot Beer’s law calibration curves for both sets of data. Explain any differences between the two curves. (Hint: Assume that P0 is 100).
9. In the process of performing a spectrophotometric determination of Fe, an analyst prepares a calibration curve using a single-beam spectrophotometer similar to that shown in Figure 10.26. After preparing the calibration curve, the analyst drops and breaks the cuvette. The analyst acquires a new cuvette, measures the absorbance of his sample, and determines the %w/w Fe in the sample. Will the change in cuvette lead to a determinate error in the analysis? Explain.
10. The spectrophotometric methods for determining Mn in steel and for determining glucose use a chemical reaction to produce a colored species whose absorbance we can monitor. In the analysis of Mn in steel, colorless Mn2+ is oxidized to give the purple MnO4– ion. To analyze for glucose, which is colorless, we react it with a yellow colored solution of the Fe(CN)63–, forming the colorless Fe(CN)64– ion. The directions for the analysis of Mn do not specify precise reaction conditions, and samples and standards may be treated separately. The conditions for the analysis of glucose, however, require that the samples and standards be treated simultaneously at exactly the same temperature and for exactly the same length of time. Explain why these two experimental procedures are so different.
11. One method for the analysis of Fe3+, which can be used with a variety of sample matrices, is to form the highly colored Fe3+–thioglycolic acid complex. The complex absorbs strongly at 535 nm. Standardizing the method is accomplished using external standards. A 10.00 ppm Fe3+ working standard is prepared by transferring a 10-mL aliquot of a 100.0 ppm stock solution of Fe3+ to a 100-mL volumetric flask and diluting to volume. Calibration standards of 1.00, 2.00, 3.00, 4.00, and 5.00 ppm are prepared by transferring appropriate amounts of the 10.0 ppm working solution into separate 50-mL volumetric flasks, each containing 5 mL of thioglycolic acid, 2 mL of 20% w/v ammonium citrate, and 5 mL of 0.22 M NH3. After diluting to volume and mixing, the absorbances of the external standards are measured against an appropriate blank. Samples are prepared for analysis by taking a portion known to contain approximately 0.1 g of Fe3+, dissolving in a minimum amount of HNO3, and diluting to volume in a 1-L volumetric flask. A 1.00-mL aliquot of this solution is transferred to a 50-mL volumetric flask, along with 5 mL of thioglycolic acid, 2 mL of 20% w/v ammonium citrate, and 5 mL of 0.22 M NH3 and diluted to volume. The absorbance of this solution is used to determine the concentration of Fe3+ in the sample.
(a) What is an appropriate blank for this procedure?
(b) Ammonium citrate is added to prevent the precipitation of Al3+. What is the effect on the reported concentration of iron in the sample if there is a trace impurity of Fe3+ in the ammonium citrate?
(c) Why does the procedure specify that the sample contain approximately 0.1 g of Fe3+?
(d) Unbeknownst to the analyst, the 100-mL volumetric flask used to prepare the 10.00 ppm working standard of Fe3+ has a volume that is significantly smaller than 100.0 mL. What effect will this have on the reported concentration of iron in the sample?
12. A spectrophotometric method for the analysis of iron has a linear calibration curve for standards of 0.00, 5.00, 10.00, 15.00, and 20.00 mg Fe/L. An iron ore sample that is 40–60% w/w is to be analyzed by this method. An approximately 0.5-g sample is taken, dissolved in a minimum of concentrated HCl, and diluted to 1 L in a volumetric flask using distilled water. A 5.00 mL aliquot is removed with a pipet. To what volume—10, 25, 50, 100, 250, 500, or 1000 mL—should it be diluted to minimize the uncertainty in the analysis? Explain.
13. Lozano-Calero and colleagues describe a method for the quantitative analysis of phosphorous in cola beverages based on the formation of the intensely blue-colored phosphomolybdate complex, (NH4)3[PO4(MoO3)12].21 The complex is formed by adding (NH4)6Mo7O24 to the sample in the presence of a reducing agent, such as ascorbic acid. The concentration of the complex is determined spectrophotometrically at a wavelength of 830 nm, using a normal calibration curve as a method of standardization.
In a typical analysis, a set of standard solutions containing known amounts of phosphorous was prepared by placing appropriate volumes of a 4.00 ppm solution of P2O5 in a 5-mL volumetric flask, adding 2 mL of an ascorbic acid reducing solution, and diluting to volume with distilled water. Cola beverages were prepared for analysis by pouring a sample into a beaker and allowing it to stand for 24 h to expel the dissolved CO2. A 2.50-mL sample of the degassed sample was transferred to a 50-mL volumetric flask and diluted to volume. A 250-μL aliquot of the diluted sample was then transferred to a 5-mL volumetric flask, treated with 2 mL of the ascorbic acid reducing solution, and diluted to volume with distilled water.
(a) The authors note that this method can be applied only to noncolored cola beverages. Explain why this is true.
(b) How might you modify this method so that it could be applied to any cola beverage?
(c) Why is it necessary to remove the dissolved gases?
(d) Suggest an appropriate blank for this method?
(e) The author’s report a calibration curve of
\[A = \mathrm{−0.02 + 0.72 × ppm\: P_2O_5}\]
A sample of Crystal Pepsi, analyzed as described above, yields an absorbance of 0.565. What is the concentration of phosphorous, reported as ppm P, in the original sample of Crystal Pepsi?
Note
Crystal Pepsi was a colorless, caffeine-free soda produced by PepsiCo. It was available in the United States from 1992 to 1993.
14. EDTA forms colored complexes with a variety of metal ions that may serve as the basis for a quantitative spectrophotometric method of analysis. The molar absorptivities of the EDTA complexes of Cu2+, Co2+, and Ni2+ at three wavelengths are summarized in the following table (all values of ε are in M–1 cm–1).
|
metal |
ε462.9 |
ε732.0 |
ε378.7 |
|
Co2+ |
15.8 |
2.11 |
3.11 |
|
Cu2+ |
2.32 |
95.2 |
7.73 |
|
Ni2+ |
1.79 |
3.03 |
13.5 |
Using this information determine the following:
(a) The concentration of Cu2+ in a solution that has an absorbance of 0.338 at a wavelength of 732.0 nm.
(b) The concentrations of Cu2+ and Co2+ in a solution that has an absorbance of 0.453 at a wavelength of 732.0 nm and 0.107 at a wavelength of 462.9 nm.
(c) The concentrations of Cu2+, Co2+, and Ni2+ in a sample that has an absorbance of 0.423 at a wavelength of 732.0 nm, 0.184 at a wavelength of 462.9 nm, and 0.291 at a wavelength of 378.7 nm.
The pathlength, b, is 1.00 cm for all measurements.
15. The concentration of phenol in a water sample is determined by separating the phenol from non-volatile impurities by steam distillation, followed by reacting with 4-aminoantipyrine and K3Fe(CN)6 at pH 7.9 to form a colored antipyrine dye. A phenol standard with a concentration of 4.00 ppm has an absorbance of 0.424 at a wavelength of 460 nm using a 1.00 cm cell. A water sample is steam distilled and a 50.00-mL aliquot of the distillate is placed in a 100-mL volumetric flask and diluted to volume with distilled water. The absorbance of this solution is found to be 0.394. What is the concentration of phenol (in parts per million) in the water sample?
16. Saito describes a quantitative spectrophotometric procedure for iron based on a solid-phase extraction using bathophenanthroline in a poly(vinyl chloride) membrane.22 In the absence of Fe2+ the membrane is colorless, but when immersed in a solution of Fe2+ and I–, the membrane develops a red color as a result of the formation of an Fe2+–bathophenanthroline complex. A calibration curve determined using a set of external standards with known concentrations of Fe2+ gave a standardization relationship of
\[A = \mathrm{(8.60×10^3\: M^{−1}) × [Fe^{2+}]}\]
What is the concentration of iron, in mg Fe/L, for a sample with an absorbance of 0.100?
17. In the DPD colorimetric method for the free chlorine residual, which is reported as mg Cl2/L, the oxidizing power of free chlorine converts the colorless amine N,N-diethyl-p-phenylenediamine to a colored dye that absorbs strongly over the wavelength range of 440–580 nm. Analysis of a set of calibration standards gave the following results.
|
mg Cl2/L |
absorbance |
|
0.00 |
0.000 |
|
0.50 |
0.270 |
|
1.00 |
0.543 |
|
1.50 |
0.813 |
|
2.00 |
1.084 |
A sample from a public water supply is analyzed to determine the free chlorine residual, giving an absorbance of 0.113. What is the free chlorine residual for the sample in mg Cl2/L?
18. Lin and Brown described a quantitative method for methanol based on its effect on the visible spectrum of methylene blue.23 In the absence of methanol, the visible spectrum for methylene blue shows two prominent absorption bands centered at approximately 610 nm and 660 nm, corresponding to the monomer and dimer, respectively. In the presence of methanol, the intensity of the dimer’s absorption band decreases, while that of the monomer increases. For concentrations of methanol between 0 and 30% v/v, the ratio of the absorbance at 663 nm, A663, to that at 610 nm, A610, is a linear function of the amount of methanol. Using the following standardization data, determine the %v/v methanol in a sample for which A610 is 0.75 and A663 is 1.07.
|
%v/v methanol |
A663/ A610 |
|
0.0 |
1.21 |
|
5.0 |
1.29 |
|
10.0 |
1.42 |
|
15.0 |
1.52 |
|
20.0 |
1.62 |
|
25.0 |
1.74 |
|
30.0 |
1.84 |
19. The concentration of the barbiturate barbital in a blood sample was determined by extracting 3.00 mL of blood with 15 mL of CHCl3. The chloroform, which now contains the barbital, is extracted with 10.0 mL of 0.45 M NaOH (pH ≈ 13). A 3.00-mL sample of the aqueous extract is placed in a 1.00-cm cell and an absorbance of 0.115 is measured. The pH of the sample in the absorption cell is then adjusted to approximately 10 by adding 0.5 mL of 16% w/v NH4Cl, giving an absorbance of 0.023. When 3.00 mL of a standard barbital solution with a concentration of 3 mg/100 mL is taken through the same procedure, the absorbance at pH 13 is 0.295 and the absorbance at a pH of 10 is 0.002. Report the mg barbital/100 mL in the sample.
20. Jones and Thatcher developed a spectrophotometric method for analyzing analgesic tablets containing aspirin, phenacetin, and caffeine.24 The sample is dissolved in CHCl3 and extracted with an aqueous solution of NaHCO3 to remove the aspirin. After the extraction is complete, the chloroform is transferred to a 250-mL volumetric flask and diluted to volume with CHCl3. A 2.00-mL portion of this solution is diluted to volume in a 200-mL volumetric flask with CHCl3. The absorbance of the final solution is measured at wavelengths of 250 nm and 275 nm, at which the absorptivities, in ppm–1 cm–1, for caffeine and phenacetin are
|
a250 |
a275 |
|
|
caffeine |
0.0131 |
0.0485 |
|
phenacetin |
0.0702 |
0.0159 |
Aspirin is determined by neutralizing the NaHCO3 in the aqueous solution and extracting the aspirin into CHCl3. The combined extracts are diluted to 500 mL in a volumetric flask. A 20.00-mL portion of the solution is placed in a 100-mL volumetric flask and diluted to volume with CHCl3. The absorbance of this solution is measured at 277 nm, where the absorptivity of aspirin is 0.00682 ppm–1 cm–1. An analgesic tablet treated by this procedure is found to have absorbances of 0.466 at 250 nm, 0.164 at 275 nm, and 0.600 at 277 nm when using a cell with a 1.00 cm pathlength. Report the milligrams of aspirin, caffeine, and phenacetin in the analgesic tablet.
21. The concentration of SO2 in a sample of air was determined by the p-rosaniline method. The SO2 was collected in a 10.00-mL solution of HgCl42–, where it reacts to form Hg(SO3)22–, by pulling the air through the solution for 75 min at a rate of 1.6 L/min. After adding p-rosaniline and formaldehyde, the colored solution was diluted to 25 mL in a volumetric flask. The absorbance was measured at 569 nm in a 1‑cm cell, yielding a value of 0.485. A standard sample was prepared by substituting a 1.00-mL sample of a standard solution containing the equivalent of 15.00 ppm SO2 for the air sample. The absorbance of the standard was found to be 0.181. Report the concentration of SO2 in the air in mg SO2/L. The density of air is 1.18 g/liter.
22. Seaholtz and colleagues described a method for the quantitative analysis of CO in automobile exhaust based on the measurement of infrared radiation at 2170 cm–1.25 A calibration curve was prepared by filling a 10-cm IR gas cell with a known pressure of CO and measuring the absorbance using an FT-IR. The standardization relationship was found to be
\[A = −1.1×10^{−4} + (9.9×10^{−4}) × P_\ce{CO}\]
Samples were prepared by using a vacuum manifold to fill the gas cell. After measuring the total pressure, the absorbance of the sample at 2170 cm–1 was measured. Results are reported as %CO (PCO/Ptotal). The analysis of five exhaust samples from a 1973 coupe give the following results.
|
Ptotal (torr) |
absorbance |
|
595 |
0.1146 |
|
354 |
0.0642 |
|
332 |
0.0591 |
|
233 |
0.0412 |
|
143 |
0.0254 |
Determine the %CO for each sample, and report the mean value and the 95% confidence interval.
23. Figure 10.32 shows an example of a disposable IR sample card made using a thin sheet of polyethylene. To prepare an analyte for analysis, it is dissolved in a suitable solvent and a portion of the sample placed on the IR card. After the solvent evaporates, leaving the analyte behind as a thin film, the sample’s IR spectrum is obtained. Because the thickness of the polyethylene film is not uniform, the primary application of IR cards is for a qualitative analysis. Zhao and Malinowski reported how an internal standardization with KSCN can be used for a quantitative IR analysis of polystyrene.26 Polystyrene was monitored at 1494 cm–1 and KSCN at 2064 cm–1. Standard solutions were prepared by placing weighed portions of polystyrene in a 10‑mL volumetric flask and diluting to volume with a solution of 10 g/L KSCN in methyl isobutyl ketone. A typical set of results is shown here.
|
g polystyrene |
0.1609 |
0.3290 |
0.4842 |
0.6402 |
0.8006 |
|
A1494 |
0.0452 |
0.1138 |
0.1820 |
0.3275 |
0.3195 |
|
A2064 |
0.1948 |
0.2274 |
0.2525 |
0.3580 |
0.2703 |
When a 0.8006-g sample of a poly(styrene/maleic anhydride) copolymer was analyzed, the following results were obtained.
|
replicate |
A1494 |
A2064 |
|
1 |
0.2729 |
0.3582 |
|
2 |
0.2074 |
0.2820 |
|
3 |
0.2785 |
0.3642 |
What is the %w/w polystyrene in the copolymer? Given that the reported %w/w polystyrene is 67%, is there any evidence for a determinate error at α = 0.05?
24. The following table lists molar absorptivities for the Arsenazo complexes of copper and barium.27 Suggest appropriate wavelengths for analyzing mixtures of copper and barium using their Arsenzao complexes.
|
wavelength (nm) |
εCu (M–1 cm–1) |
εBa (M–1 cm–1) |
|
595 |
11900 |
7100 |
|
600 |
15500 |
7200 |
|
607 |
18300 |
7400 |
|
611 |
19300 |
6900 |
|
614 |
19300 |
7000 |
|
620 |
17800 |
7100 |
|
626 |
16300 |
8400 |
|
635 |
10900 |
9900 |
|
641 |
7500 |
10500 |
|
645 |
5300 |
10000 |
|
650 |
3500 |
8600 |
|
655 |
2200 |
6600 |
|
658 |
1900 |
6500 |
|
665 |
1500 |
3900 |
|
670 |
1500 |
2800 |
|
680 |
1800 |
1500 |
25. Blanco and colleagues report several applications of multiwavelength linear regression analysis for the simultaneous determination of two-component mixtures.9 For each of the following, determine the molar concentration of each analyte in the mixture.
(a) Titanium and vanadium were determined by forming complexes with H2O2. Results for a mixture of Ti(IV) and V(V) and for standards of 63.1 ppm Ti(IV) and 96.4 ppm V(V) are listed in the following table.
|
absorbance |
|||
|
wavelength (nm) |
Ti(V) standard |
V(V) standard |
mixture |
|
390 |
0.895 |
0.326 |
0.651 |
|
430 |
0.884 |
0.497 |
0.743 |
|
450 |
0.694 |
0.528 |
0.665 |
|
470 |
0.481 |
0.512 |
0.547 |
|
510 |
0.173 |
0.374 |
0.314 |
(b) Copper and zinc were determined by forming colored complexes with 2-pyridyl-azo-resorcinol (PAR). The absorbances for PAR, a mixture of Cu2+ and Zn2+, and standards of 1.00 ppm Cu2+ and 1.00 ppm Zn2+ are listed in the following table. Note that you must correct the absorbances for the metal for the contribution from PAR.
|
absorbance |
||||
|
wavelength (nm) |
PAR |
Cu standard |
Zn standard |
mixture |
|
480 |
0.211 |
0.698 |
0.971 |
0.656 |
|
496 |
0.137 |
0.732 |
1.018 |
0.668 |
|
510 |
0.100 |
0.732 |
0.891 |
0.627 |
|
526 |
0.072 |
0.602 |
0.672 |
0.498 |
|
540 |
0.056 |
0.387 |
0.306 |
0.290 |
26. The stoichiometry of a metal–ligand complex, MLn, was determined by the method of continuous variations. A series of solutions was prepared in which the combined concentrations of M and L were held constant at 5.15 × 10–4 M. The absorbances of these solutions were measured at a wavelength where only the metal–ligand complex absorbs. Using the following data, determine the formula of the metal–ligand complex.
|
mole fraction M |
mole fraction L |
absorbance |
|
1.0 |
0.0 |
0.001 |
|
0.9 |
0.1 |
0.126 |
|
0.8 |
0.2 |
0.260 |
|
0.7 |
0.3 |
0.389 |
|
0.6 |
0.4 |
0.515 |
|
0.5 |
0.5 |
0.642 |
|
0.4 |
0.6 |
0.775 |
|
0.3 |
0.7 |
0.771 |
|
0.2 |
0.8 |
0.513 |
|
0.1 |
0.9 |
0.253 |
|
0.0 |
1.0 |
0.000 |
27. The stoichiometry of a metal–ligand complex, MLn, was determined by the mole-ratio method. A series of solutions was prepared in which the concentration of metal was held constant at 3.65 × 10–4 M, and the ligand’s concentration was varied from 1 × 10–4 M to 1 × 10–3 M. Using the following data, determine the stoichiometry of the metal-ligand complex.
|
[ligand] (M) |
absorbance |
|
1.0×10–4 |
0.122 |
|
2.0×10–4 |
0.251 |
|
3.0×10–4 |
0.376 |
|
4.0×10–4 |
0.496 |
|
5.0×10–4 |
0.625 |
|
6.0×10–4 |
0.752 |
|
7 .0×10–4 |
0.873 |
|
8 .0×10–4 |
0.937 |
|
9 .0×10–4 |
0.962 |
|
1 .0×10–3 |
1.002 |
28. The stoichiometry of a metal–ligand complex, MLn, was determined by the slope-ratio method. Two sets of solutions were prepared. For the first set of solutions the concentration of the metal was held constant at 0.010 M and the concentration of the ligand was varied. When the absorbance of these solutions was measured at a wavelength where only the metal–ligand complex absorbs, the following data were obtained.
|
[ligand] (M) |
absorbance |
|
1.0×10–5 |
0.012 |
|
2.0×10–5 |
0.029 |
|
3.0×10–5 |
0.042 |
|
4.0×10–5 |
0.055 |
|
5.0×10–5 |
0.069 |
For the second set of solutions the concentration of the ligand was held constant at 0.010 M, and the concentration of the metal was varied, yielding the following absorbances.
|
[metal] (M) |
absorbance |
|
1.0×10–5 |
0.040 |
|
2.0×10–5 |
0.085 |
|
3.0×10–5 |
0.125 |
|
4.0×10–5 |
0.162 |
|
5.0×10–5 |
0.206 |
Using this data, determine the stoichiometry of the metal-ligand complex.
29. Kawakami and Igarashi developed a spectrophotometric method for nitrite based on its reaction with 5, 10, 15, 20-tetrakis(4-aminophenyl)porphrine (TAPP). As part of their study they investigated the stoichiometry of the reaction between TAPP and NO2–. The following data are derived from a figure in their paper.28
|
[TAPP] (M) |
[NO2−] (M) |
absorbance |
|
8.0×10–7 |
1.6×10–7 |
0.227 |
|
8.0×10–7 |
3.2×10–7 |
0.192 |
|
8.0×10–7 |
4.8×10–7 |
0.158 |
|
8.0×10–7 |
8.0×10–7 |
0.126 |
|
8.0×10–7 |
1.6×10–6 |
0.065 |
|
8.0×10–7 |
2.4×10–6 |
0.047 |
|
8.0×10–7 |
3.2×10–6 |
0.042 |
|
8.0×10–7 |
4.0×10–6 |
0.042 |
What is the stoichiometry of the reaction?
30. The equilibrium constant for an acid–base indicator is determined by preparing three solutions, each of which has a total indicator concentration of 1.35× 10–5 M. The pH of the first solution is adjusted until it is acidic enough to ensure that only the acid form of the indicator is present, yielding an absorbance of 0.673. The absorbance of the second solution, whose pH is adjusted to give only the base form of the indicator, is 0.118. The pH of the third solution is adjusted to 4.17 and has an absorbance of 0.439. What is the acidity constant for the acid–base indicator?
31. The acidity constant for an organic weak acid was determined by measuring its absorbance as a function of pH while maintaining a constant total concentration of the acid. Using the data in the following table, determine the acidity constant for the organic weak acid.
|
pH |
absorbance |
|
1.53 |
0.010 |
|
2.20 |
0.010 |
|
3.66 |
0.035 |
|
4.11 |
0.072 |
|
4.35 |
0.103 |
|
4.75 |
0.169 |
|
4.88 |
0.193 |
|
5.09 |
0.227 |
|
5.69 |
0.288 |
|
7.20 |
0.317 |
|
7.78 |
0.317 |
32. Suppose you need to prepare a set of calibration standards for the spectrophotometric analysis of an analyte that has a molar absorptivity of 1138 M–1 cm–1 at a wavelength of 625 nm. To maintain an acceptable precision for the analysis, the %T for the standards should be between 15% and 85%.
(a) What is the concentration of the most concentrated and the least concentrated standard you should prepare, assuming a 1.00-cm sample cell.
(b) Explain how you will analyze samples with concentrations that are 10 μM, 0.1 mM, and 1.0 mM in the analyte.
33. When using a spectrophotometer whose precision is limited by the uncertainty of reading %T, the analysis of highly absorbing solutions can lead to an unacceptable level of indeterminate errors. Consider the analysis of a sample for which the molar absorptivity is 1.0 × 104 M–1 cm–1 and the pathlength is 1.00 cm.
(a) What is the relative uncertainty in concentration for an analyte whose concentration is 2.0 × 10–4 M if sT is ±0.002?
(b) What is the relative uncertainty in the concentration if the spectrophotometer is calibrated using a blank consisting of a 1.0 × 10–4 M solution of the analyte?
34. Hobbins reported the following calibration data for the flame atomic absorption analysis for phosphorous.29
|
mg P / L |
absorbance |
|
2130 |
0.048 |
|
4260 |
0.110 |
|
6400 |
0.173 |
|
8530 |
0.230 |
To determine the purity of a sample of Na2HPO4, a 2.469-g sample is dissolved and diluted to volume in a 100-mL volumetric flask. Analysis of the resulting solution gives an absorbance of 0.135. What is the purity of the Na2HPO4?
35. Bonert and Pohl reported results for the atomic absorption analysis of several metals in the caustic suspensions produced during the manufacture of soda by the ammonia-soda process.30
(a) The concentration of Cu was determined by acidifying a 200-mL sample of the caustic solution with 20 mL of concentrated HNO3, adding 1 mL of 27% w/v H2O2, and boiling for 30 min. The resulting solution was diluted to 500 mL, filtered, and analyzed by flame atomic absorption using matrix matched standards. The results for a typical analysis are shown in the following table.
|
solution |
mg Cu / L |
absorbance |
|
blank |
0.000 |
0.007 |
|
standard 1 |
0.200 |
0.014 |
|
standard 2 |
0.500 |
0.036 |
|
standard 3 |
1.000 |
0.072 |
|
standard 4 |
2.000 |
0.146 |
|
sample |
0.027 |
Determine the concentration of Cu in the caustic suspension.
(b) The determination of Cr was accomplished by acidifying a 200-mL sample of the caustic solution with 20 mL of concentrated HNO3, adding 0.2 g of Na2SO3 and boiling for 30 min. The Cr was isolated from the sample by adding 20 mL of NH3, producing a precipitate that includes the chromium as well as other oxides. The precipitate was isolated by filtration, washed, and transferred to a beaker. After acidifying with 10 mL of HNO3, the solution was evaporated to dryness. The residue was redissolved in a combination of HNO3 and HCl and evaporated to dryness. Finally, the residue was dissolved in 5 mL of HCl, filtered, diluted to volume in a 50-mL volumetric flask, and analyzed by atomic absorption using the method of standard additions. The atomic absorption results are summarized in the following table.
|
sample |
mg Cradded / L |
absorbance |
|
blank |
0.001 |
|
|
sample |
0.045 |
|
|
standard addition 1 |
0.200 |
0.083 |
|
standard addition 2 |
0.500 |
0.118 |
|
standard addition 3 |
1.000 |
0.192 |
Report the concentration of Cr in the caustic suspension.
36. Quigley and Vernon report results for the determination of trace metals in seawater using a graphite furnace atomic absorption spectrophotometer and the method of standard additions.31 The trace metals were first separated from their complex, high-salt matrix by coprecipitating with Fe3+. In a typical analysis a 5.00-mL portion of 2000 ppm Fe3+ was added to 1.00 L of seawater. The pH was adjusted to 9 using NH4OH, and the precipitate of Fe(OH)3 allowed to stand overnight. After isolating and rinsing the precipitate, the Fe(OH)3 and coprecipitated metals were dissolved in 2 mL of concentrated HNO3 and diluted to volume in a 50-mL volumetric flask. To analyze for Mn2+, a 1.00-mL sample of this solution was diluted to 100 mL in a volumetric flask. The following samples were injected into the graphite furnace and analyzed.
|
sample |
absorbance |
|
2.5-μL sample + 2.5 μL of 0 ppb Mn2+ |
0.223 |
|
2.5-μL sample + 2.5 μL of 2.5 ppb Mn2+ |
0.294 |
|
2.5-μL sample + 2.5 μL of 5.0 ppb Mn2+ |
0.361 |
Report the parts per billion Mn2+ in the sample of seawater.
37. The concentration of Na in plant materials may be determined by flame atomic emission. The material to be analyzed is prepared by grinding, homogenizing, and drying at 103oC. A sample of approximately 4 g is transferred to a quartz crucible and heated on a hot plate to char the organic material. The sample is heated in a muffle furnace at 550oC for several hours. After cooling to room temperature the residue is dissolved by adding 2 mL of 1:1 HNO3 and evaporated to dryness. The residue is redissolved in 10 mL of 1:9 HNO3, filtered and diluted to 50 mL in a volumetric flask. The following data were obtained during a typical analysis for the concentration of Na in a 4.0264-g sample of oat bran.
|
sample |
mg Na / L |
emission (arbitrary units) |
|
blank |
0.00 |
0.0 |
|
standard 1 |
2.00 |
90.3 |
|
standard 2 |
4.00 |
181 |
|
standard 3 |
6.00 |
272 |
|
standard 4 |
8.00 |
363 |
|
standard 5 |
10.00 |
448 |
|
sample |
238 |
Determine the mg Na/L in the sample of oat bran.
38. Gluodenis describes the use of ICP atomic emission to analyze samples of brass for Pb and Ni.32 The analysis for Pb uses external standards prepared from brass samples containing known amounts of lead. Results are shown in the following table.
|
%w/w Pb |
emission intensity |
| 0.000 | 4.29 × 104 |
| 0.0100 | 1.87 × 105 |
| 0.0200 | 3.20 × 105 |
| 0.0650 | 1.28 × 106 |
| 0.350 | 6.22 × 106 |
| 0.700 | 1.26 × 107 |
| 1.04 | 1.77 × 107 |
| 2.24 | 3.88 × 107 |
| 3.15 | 5.61 × 107 |
| 9.25 | 1.64 × 108 |
What is the %w/w Pb in a sample of brass that gives an emission intensity of 9.25 × 104?
The analysis for Ni uses an internal standard. Results for a typical calibration are show in the following table.
|
% w/w Ni |
emission intensity ratio |
|
0.000 |
0.00267 |
|
0.0140 |
0.00154 |
|
0.0330 |
0.00312 |
|
0.130 |
0.120 |
|
0.280 |
0.246 |
|
0.280 |
0.247 |
|
0.560 |
0.533 |
|
1.30 |
1.20 |
|
4.82 |
4.44 |
What is the %w/w Ni in a sample for which the ratio of emission intensity is 1.10 × 10–3?
39. Yan and colleagues developed a method for the analysis of iron based its formation of a fluorescent metal–ligand complex with the ligand 5-(4-methylphenylazo)-8-aminoquinoline.33 In the presence of the surfactant cetyltrimethyl ammonium bromide the analysis is carried out using an excitation wavelength of 316 nm with emission monitored at 528 nm. Standardization with external standards gives the following calibration curve.
\[I_\ce{f} = \mathrm{−0.03 + 1.594 × \dfrac{mg\: Fe^{3+}}{L}}\]
A 0.5113-g sample of dry dog food was ashed to remove organic materials, and the residue dissolved in a small amount of HCl and diluted to volume in a 50-mL volumetric flask. Analysis of the resulting solution gave a fluorescent emission intensity of 5.72. Determine the mg Fe/L in the sample of dog food.
40. A solution of 5.00 × 10–5 M 1,3-dihydroxynaphthelene in 2 M NaOH has a fluorescence intensity of 4.85 at a wavelength of 459 nm. What is the concentration of 1,3-dihydroxynaphthelene in a solution with a fluorescence intensity of 3.74 under identical conditions?
41. The following data was recorded for the phosphorescence intensity for several standard solutions of benzo[a]pyrene.
|
[benzo[a]pyrene] (M) |
emission intensity |
|
0 |
0.00 |
|
1.00×10–5 |
0.98 |
|
3.00×10–5 |
3.22 |
|
6.00×10–5 |
6.25 |
|
1.00×10–4 |
10.21 |
What is the concentration of benzo[a]pyrene in a sample yielding a phosphorescent emission intensity of 4.97?
42. The concentration of acetylsalicylic acid, C9H8O4, in aspirin tablets can be determined by hydrolyzing to the salicylate ion, C7H5O2–, and determining the concentration of the salicylate ion spectrofluorometrically. A stock standard solution is prepared by weighing 0.0774 g of salicylic acid, C7H6O2, into a 1-L volumetric flask and diluting to volume with distilled water. A set of calibration standards is prepared by pipeting 0, 2.00, 4.00, 6.00, 8.00, and 10.00 mL of the stock solution into separate 100-mL volumetric flasks containing 2.00 mL of 4 M NaOH and diluting to volume with distilled water. The fluorescence of the calibration standards was measured at an emission wavelength of 400 nm using an excitation wavelength of 310 nm; results are listed in the following table.
|
mL of stock solution |
emission intensity |
|
0.00 |
0.00 |
|
2.00 |
3.02 |
|
4.00 |
5.98 |
|
6.00 |
9.18 |
|
8.00 |
12.13 |
|
10.00 |
14.96 |
Several aspirin tablets are ground to a fine powder in a mortar and pestle. A 0.1013-g portion of the powder is placed in a 1-L volumetric flask and diluted to volume with distilled water. A portion of this solution is filtered to remove insoluble binders and a 10.00-mL aliquot transferred to a 100-mL volumetric flask containing 2.00 mL of 4 M NaOH. After diluting to volume the fluorescence of the resulting solution is found to be 8.69. What is the %w/w acetylsalicylic acid in the aspirin tablets?
43. Selenium (IV) in natural waters can be determined by complexing with ammonium pyrrolidine dithiocarbamate and extracting into CHCl3. This step serves to concentrate the Se(IV) and to separate it from Se(VI). The Se(IV) is then extracted back into an aqueous matrix using HNO3. After complexing with 2,3-diaminonaphthalene, the complex is extracted into cyclohexane. Fluorescence is measured at 520 nm following its excitation at 380 nm. Calibration is achieved by adding known amounts of Se(IV) to the water sample before beginning the analysis. Given the following results what is the concentration of Se(IV) in the sample.
|
[Se(IV)] added (nM) |
emission intensity |
|
0.00 |
323 |
|
2.00 |
597 |
|
4.00 |
862 |
|
6.00 |
1123 |
44. Fibrinogen is a protein that is produced by the liver and found in human plasma. Its concentration in plasma is clinically important. Many of the analytical methods used to determine the concentration of fibrinogen in plasma are based on light scattering following its precipitation. For example, da Silva and colleagues describe a method in which fibrinogen precipitates in the presence of ammonium sulfate in a guanidine hydrochloride buffer.34 Light scattering is measured nephelometrically at a wavelength of 340 nm. Analysis of a set of external calibration standards gives the following calibration equation
\[I_\ce{s} = −4.66 + 9907.63 × C\]
where Is is the intensity of scattered light and C is the concentration of fibrinogen in g/L. A 9.00-mL sample of plasma was collected from a patient and mixed with 1.00 mL of an anticoagulating agent. A 1.00-mL aliquot of this solution was then diluted to 250 mL in a volumetric flask. Analysis of the resulting solution gave a scattering intensity of 44.70. What is the concentration of fibrinogen, in gram per liter, in the plasma sample?
10.9.3 Solutions to Practice Exercises
Practice Exercise 10.1
The frequency and wavenumber for the line are
\[ν = \dfrac{c}{λ} = \mathrm{\dfrac{3.00×10^8\: m/s}{656.3×10^{−9}\:m} = 4.57×10^{14}\: s^{−1}}\]
\[\overline{ν} = \dfrac{1}{λ} = \mathrm{\dfrac{1}{656.3×10^{−9}\: m} × \dfrac{1\: m}{100\: cm} = 1.524×10^4\: cm^{−1}}\]
Click here to return to the chapter.
Practice Exercise 10.2
The photon’s energy is
\[E = \dfrac{hc}{λ} = \mathrm{\dfrac{(6.626×10^{−34}\: J⋅s)(3.00×10^8\: m/s)}{656.3×10^{−9}\: m} = 3.03×10^{−19}\: J}\]
Click here to return to the chapter.
Practice Exercise 10.3
To find the transmittance, T, we begin by noting that
\[A = 1.27 = -\log T\]
Solving for T
\[–1.27 = \log T\]
\[10^{–1.27} = T\]
gives a transmittance of 0.054, or a %T of 5.4%.
Click here to return to the chapter.
Practice Exercise 10.4
Making appropriate substitutions into Beer’s law
\[A = 0.228 = εbC= \mathrm{(676\: M^{–1}\: cm^{–1})(1\: cm)}C\]
and solving for C gives a concentration of 3.37×10-4 M.
Click here to return to the chapter.
Practice Exercise 10.5
For this standard addition we can write the following equations relating absorbance to the concentration of Cu2+ in the sample. First, for the sample, we have
\[0.118 = εbC_\ce{Cu}\]
and for the standard addition we have
\[0.162 = εb\left(C_\ce{Cu} + \mathrm{\dfrac{20.00\: mg\: Cu}{L} × \dfrac{1.00\: mL}{10.00\: mL}}\right)\]
The value of εb is the same in both equation. Solving each equation for εb and equating
\[\dfrac{0.162}{C_\ce{Cu} + \mathrm{\dfrac{20.00\: mg\: Cu}{L} × \dfrac{1.00\: mL}{10.00\: mL}}} = \dfrac{0.118}{C_\ce{Cu}}\]
leaves us with an equation in which CCu is the only variable. Solving for CCu gives its value as
\[\dfrac{0.162}{C_\ce{Cu} + \mathrm{2.00\: mg\: Cu/L}} = \dfrac{0.118}{C_\ce{Cu}}\]
\[0.162C_\ce{Cu} = 0.118C_\ce{Cu} + \mathrm{0.236\: mg\: Cu/L}\]
\[0.044C_\ce{Cu} = \mathrm{0.236\: mg\: Cu/L}\]
\[C_\ce{Cu} = \mathrm{5.4\: mg\: Cu/L}\]
Click here to return to the chapter.
Practice Exercise 10.6
Substituting into equation 10.11 and equation 10.12 gives
\[A_{400}= 0.336 = 15.2C_\ce{Cr} + 5.60C_\ce{Co}\]
\[A_{505} = 0.187 = 0.533C_\ce{Cr} + 5.07C_\ce{Co}\]
To determine CCr and CCo we solve the first equation for CCo
\[C_\ce{Co} = \dfrac{0.336 − 15.2C_\ce{Cr}}{5.60}\]
and substitute the result into the second equation.
\[0.187 = 0.533C_\ce{Cr} + 5.07 × \dfrac{0.336 − 15.2C_\ce{Cr}}{5.60} = 0.3042 − 13.23C_\ce{Cr}\]
Solving for CCr gives the concentration of Cr3+ as 8.86 × 10–3 M. Substituting this concentration back into the equation for the mixture’s absorbance at 400 nm gives the concentration of Co2+ as 3.60 × 10–2 M.
Click here to return to the chapter.
Practice Exercise 10.7
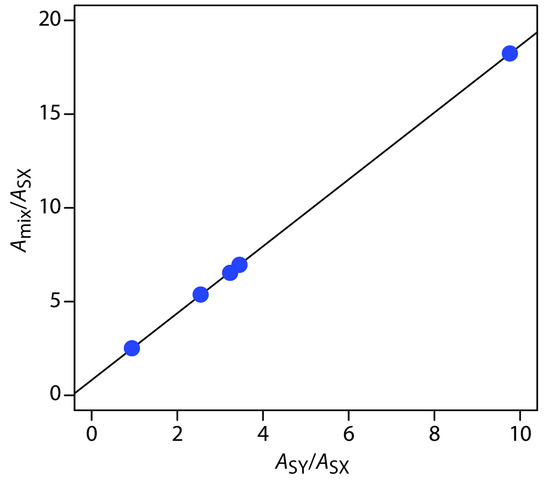
Letting X represent MnO4– and Y represent Cr2O72–, we plot the equation
\[\dfrac{A_\ce{mix}}{A_\ce{SX}} = \dfrac{C_\ce{X}}{C_\ce{SX}} + \dfrac{C_\ce{Y}}{C_\ce{SY}} × \dfrac{A_\ce{SY}}{A_\ce{SX}}\]
placing Amix/ASX on the y-axis and ASY/ASX on the x-axis. For example, at a wavelength of 266 nm the value of Amix/ASX is 0.766/0.042, or 18.2, and the value of ASY/ASX is 0.410/0.042, or 9.76. Completing the calculations for all wavelengths and plotting the data gives the result shown in Figure 10.67. Fitting a straight-line to the data gives a regression model of
\[\dfrac{A_\ce{mix}}{A_\ce{SX}} = 0.8147 + 1.7839 × \dfrac{A_\ce{SY}}{A_\ce{SX}}\]
Using the y-intercept, the concentration of MnO4–is
\[\dfrac{C_\ce{X}}{C_\ce{SX}} = \dfrac{[\ce{MnO4-}]}{1.0×10^{−4}\:\ce{M\: MnO_4^-} = 0.8147}\]
or 8.15 × 10–5 M MnO4–, and using the slope, the concentration of Cr2O72– is
\[\dfrac{C_\ce{Y}}{C_\ce{SY}}= \dfrac{[\ce{Cr2O7^2-}]}{1.0×10^{−4}\: \ce{M\: Cr2O7^2-}} = 1.7839\]
or 1.78×10–4 M Cr2O72–.
Figure 10.67 Multiwavelength linear regression analysis for the data in Practice Exercise 10.7.
Click here to return to the chapter.
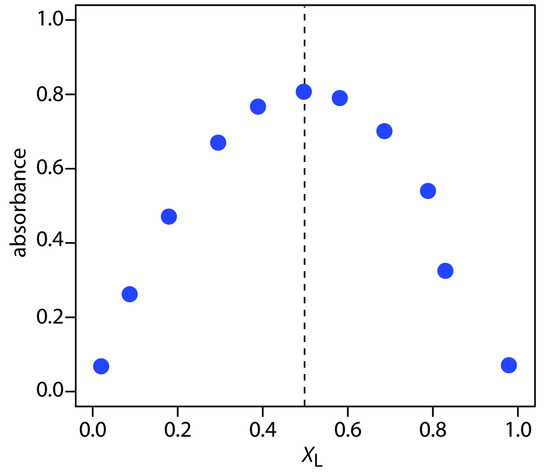
Practice Exercise 10.8
Figure 10.68 shows a continuous variations plot for the data in this exercise. Although the individual data points show substantial curvature—enough curvature that there is little point in trying to draw linear branches for excess metal and excess ligand—the maximum absorbance clearly occurs at an XL of approximately 0.5. The complex’s stoichiometry, therefore, is Fe(SCN)2+.
Figure 10.68 Continuous variations plot for the data in Practice Exercise 10.8.
Click here to return to the chapter.
Practice Exercise 10.9
The value of Ka is
\[K_\ce{a} = (1.00×10^{−6}) × \dfrac{0.225 − 0.000}{0.680 − 0.225} = 4.95×10^{−7}\]
Click here to return to the chapter.
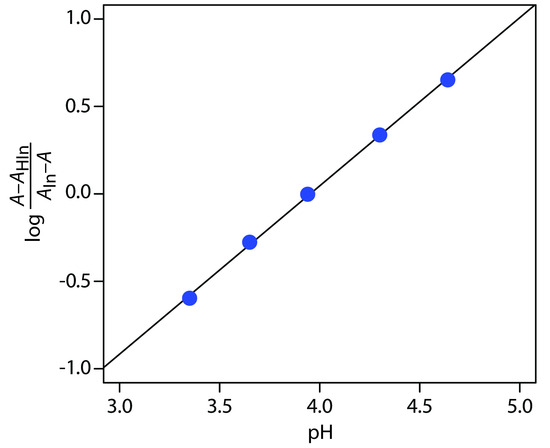
Practice Exercise 10.10
To determineKa we use equation 10.21, plotting log[(A – AHIn) / (AIn – A)] versus pH, as shown in Figure 10.69. Fitting a straight-line to the data gives a regression model of
\[\log\dfrac{A − A_\ce{HIn}}{A_\ce{In} − A} = \mathrm{−3.80 + 0.962pH}\]
The y-intercept is –pKa; thus, the pKa is 3.80 and the Ka is 1.58×10–4.
Figure 10.69 Determining the pKa of bromothymol blue using the data in Practice Exercise 10.10.
Click here to return to the chapter.