7.E: Collecting and Preparing Samples (Exercises)
- Page ID
- 70450
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
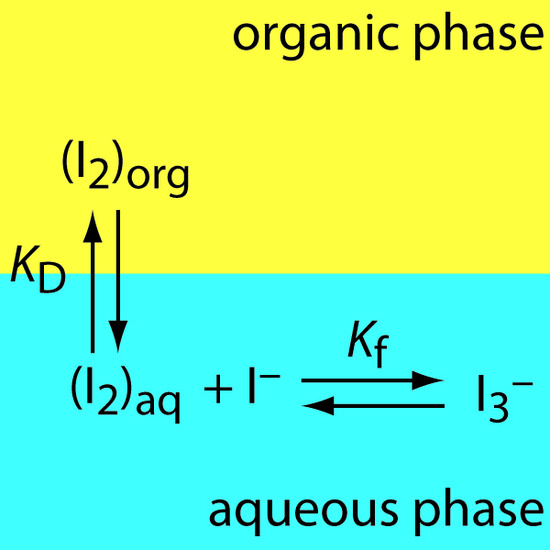
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)1. Because of the risk of lead poisoning, the exposure of children to lead-based paint is a significant public health concern. The first step in the quantitative analysis of lead in dried paint chips is to dissolve the sample. Corl has evaluated several dissolution techniques.22 In this study, samples of paint were collected and pulverized with a Pyrex mortar and pestle. Replicate portions of the powdered paint were then taken for analysis. The following table shows results for a paint sample and for a standard reference material. Both samples and standards were digested with HNO3 on a hot plate.
| Replicate | % w/w Pb in Sample |
% w/w Pb in Standard |
| 1 | 5.09 | 11.48 |
| 2 | 6.29 | 11.62 |
| 3 | 6.64 | 11.47 |
| 4 | 4.63 | 11.86 |
(a) Determine the overall variance, the variance due to the method and the variance due to sampling. (b) What percentage of the overall variance is due to sampling? (c) How might you decrease the variance due to sampling?
2. To analyze a shipment of 100 barrels of an organic solvent, you plan to collect and analyze single samples from ten barrels using a random sampling. From which barrels should you collect samples if the first barrel is given by the 12th entry in the random number table in Appendix 14, with subsequent barrels given by every third entry? Assume that entries in the random number table are arranged by rows.
3. The concentration of dissolved O2 in a lake shows a daily cycle from the effect of photosynthesis, and a yearly cycle due to seasonal changes in temperature. Suggest an appropriate systematic sampling plan for monitoring the daily change in dissolved O2. Suggest an appropriate systematic sampling plan for monitoring the yearly change in dissolved O2.
4. The data in the following table were collected during a preliminary study of the pH of an industrial wastewater stream.
|
Time (h) |
pH |
Time (h) |
pH |
|
0.5 |
4.4 |
9.0 |
5.7 |
|
1.0 |
4.8 |
9.5 |
5.5 |
|
1.5 |
5.2 |
10.0 |
6.5 |
|
2.0 |
5.2 |
10.5 |
6.0 |
|
2.5 |
5.6 |
11.0 |
5.8 |
|
3.0 |
5.4 |
11.5 |
6.0 |
|
3.5 |
5.4 |
12.0 |
5.6 |
|
4.0 |
4.4 |
12.5 |
5.6 |
|
4.5 |
4.8 |
13.0 |
5.4 |
|
5.0 |
4.8 |
13.5 |
4.9 |
|
5.5 |
4.2 |
14.0 |
5.2 |
|
6.0 |
4.2 |
14.5 |
4.4 |
|
6.5 |
3.8 |
15.0 |
4.0 |
|
7.0 |
4.0 |
15.5 |
4.5 |
|
7.5 |
4.0 |
16.0 |
4.0 |
|
8.0 |
3.9 |
16.5 |
5.0 |
|
8.5 |
4.7 |
17.0 |
5.0 |
Construct a graph of pH as a function of time and suggest an appropriate sampling frequency for a long-term monitoring program.
5. You have been asked to monitor the daily fluctuations in atmospheric ozone in the downtown area of a city to determine if there is relationship between daily traffic patterns and ozone levels. (a) Which of the following sampling plan will you use: random, systematic, judgmental, systematic–judgmental, or stratified? (b) Do you plan to collect and analyze a series of grab samples, or will you form a single composite sample? (c) Will your answers to these questions change if your goal is to determine if the average daily ozone level exceeds a threshold value? If your answer is yes, then what is your new sampling strategy?
6. The distinction between a homogeneous population and a heterogeneous population is important when you are developing a sampling plan. (a) Define homogeneous and heterogeneous. (b) If you collect and analyze a single sample, can you determine if the population is homogeneous or heterogeneous?
7. The sampling of a heterogeneous population is particularly challenging. Explain why you can minimize the sampling variance for a heterogeneous population by increasing the number of samples, but not by increasing the mass of individual samples.
8. Beginning with equation 7.4, derive equation 7.5. Assume that the particles are spherical with a radius of r and a density of d.
9. The sampling constant for the radioisotope 24Na in homogenized human liver has been reported as approximately 35 g.23 (a) What is the expected relative standard deviation for sampling if you analyze 1.0-g samples? (b) How many 1.0-g samples must you analyze to obtain a maximum sampling error of ±5% at the 95% confidence level?
10. Engels and Ingamells reported the following results for the % w/w K2O in a mixture of amphibolite and orthoclase.24
|
0.247 |
0.300 |
0.236 |
0.258 |
0.304 |
0.330 |
|
0.247 |
0.275 |
0.212 |
0.311 |
0.258 |
0.187 |
Each of the 12 samples had a nominal weight of 0.1 g. Determine the approximate value for Ks and the mass of sample needed to achieve a percent relative standard deviation of 2%.
11. The following data has been reported for the determination of KH2PO4 in a mixture of KH2PO4 and NaCl.25
| Nominal Mass (g) | Actual Mass (g) | % w/w KH2PO4 |
|
0.10 |
0.1039 0.1015 0.1012 0.1010 0.1060 0.0997 |
0.085 1.078 0.413 1.248 0.654 0.507 |
|
0.25 |
0.2515 0.2465 0.2770 0.2460 0.2485 0.2590 |
0.847 0.598 0.431 0.842 0.964 1.178 |
|
0.50 |
0.5084 0.4954 0.5286 0.5232 0.4965 0.4995 |
1.009 0.947 0.618 0.744 0.572 0.709 |
|
1.00 |
1.027 0.987 0.991 0.998 0.997 1.001 |
0.696 0.843 0.535 0.750 0.711 0.639 |
|
2.50 |
2.496 2.504 2.496 2.496 2.557 2.509 |
0.766 0.769 0.682 0.609 0.589 0.617 |
(a) Prepare a graph of % w/w KH2PO4 versus the actual sample mass and discuss how this graph is consistent with your understanding of the factors affecting sampling variance. (b) For each nominal mass, calculate the percent relative standard deviation for the analysis. The value of Ks for this analysis has been estimated as 350. For each nominal mass, use this Ks to determine the percent relative standard deviation due to sampling. Considering these calculations, what is your conclusion about the importance of indeterminate sampling errors for this analysis? (c) For each nominal mass, convert the percent relative standard deviation to an absolute standard deviation. Plot points on your graph corresponding to ±1 absolute standard deviations about the overall average % w/w KH2PO4. Draw smooth curves through these two sets of points. Considering these curves, does the sample appear to be homogeneous on the scale at which it is sampled?
12. In this problem you will collect and analyze data in a simulation of the sampling process. Obtain a pack of M&M’s (or other similar candy). Collect a sample of five candies and count the number that are red (or any other color of your choice). Report the result of your analysis as % red. Return the candies to the bag, mix thoroughly, and repeat the analysis for a total of 20 determinations. Calculate the mean and the standard deviation for your data. Remove all candies from the bag and determine the true % red for the population. Sampling in this exercise should follow binomial statistics. Calculate the expected mean value and the expected standard deviation, and compare to your experimental results.
13. Determine the error (α = 0.05) for the following situations. In each case assume that the variance for a single determination is 0.0025 and that the variance for collecting a single sample is 0.050. (a) Nine samples are collected, each analyzed once. (b) One sample is collected and analyzed nine times. (c) Three samples are collected, each analyzed three times.
14. Which of the sampling schemes in problem 13 is best if you wish to limit the overall error to less than ±0.25, and the cost of collecting a single sample is 1 (arbitrary units), and the cost of analyzing a single sample is 10? Which is the best sampling scheme if the cost of collecting a single sample is 7, and the cost of analyzing a single sample is 3?
15. Maw, Witry, and Emond evaluated a microwave digestion method for Hg against the standard open-vessel digestion method.26 The standard method requires a 2-h digestion and is operator-intensive. The microwave digestion is complete in approximately 0.5 h and requires little monitoring by the operator. Samples of baghouse dust from air-pollution-control equipment were collected from a hazardous waste incinerator and digested in triplicate before determining the concentration of Hg in ppm. Results are summarized in the following tables.
|
ppm Hg Following Microwave Digestion |
|||
|
Sample |
Replicate 1 |
Replicate 2 |
Replicate 3 |
|
1 |
7.12 |
7.66 |
7.17 |
|
2 |
16.1 |
15.7 |
15.6 |
|
3 |
4.89 |
4.62 |
4.28 |
|
4 |
9.64 |
9.03 |
8.44 |
|
5 |
6.76 |
7.22 |
7.50 |
|
6 |
6.19 |
6.61 |
7.61 |
|
7 |
9.44 |
9.56 |
10.7 |
|
8 |
30.8 |
29.0 |
26.2 |
|
ppm Hg Following Standard Digestion |
|||
|
Sample |
Replicate 1 |
Replicate 2 |
Replicate 3 |
|
1 |
5.50 |
5.54 |
5.40 |
|
2 |
13.1 |
12.8 |
13.0 |
|
3 |
5.39 |
5.12 |
5.36 |
|
4 |
6.59 |
6.52 |
7.20 |
|
5 |
6.20 |
6.03 |
5.77 |
|
6 |
6.25 |
5.65 |
5.61 |
|
7 |
15.0 |
13.9 |
14.0 |
|
8 |
20.4 |
16.1 |
20.0 |
Does the microwave digestion method yields acceptable results in comparison to the standard digestion method?
16. Simpson, Apte, and Batley investigated methods for preserving water samples collected from anoxic (O2-poor) environments that contain high concentrations of dissolved sulfide.27 They found that preserving water samples with HNO3 (a common method for preserving aerobic samples) gave significant negative determinate errors when analyzing for Cu2+. Preserving samples by first adding H2O2 and then adding HNO3, eliminated the determinate error. Explain their observations.
17. In a particular analysis the selectivity coefficient, KA,I, is 0.816. When a standard sample with an analyte-to-interferent ratio of 5:1 is carried through the analysis, the error in determining the analyte is +6.3%. (a) Determine the apparent recovery for the analyte if RI = 0. (b) Determine the apparent recovery for the interferent if RA = 0.
18. The amount of Co in an ore is to be determined using a procedure for which Fe in an interferent. To evaluate the procedure’s accuracy, a standard sample of ore known to have a Co/Fe ratio of 10.2:1 is analyzed. When pure samples of Co and Fe are taken through the procedure the following calibration relationships are obtained
\[S_\textrm{Co}=0.786\times m_\textrm{Co}\]
\[S_\textrm{Fe}=0.669\times m_\textrm{Fe}\]
where S is the signal and m is the mass of Co or Fe. When 278.3 mg of Co are taken through the separation step, 275.9 mg are recovered. Only 3.6 mg of Fe are recovered when a 184.9 mg sample of Fe is carried through the separation step. Calculate (a) the recoveries for Co and Fe; (b) the separation factor; (c) the error if no attempt is made to separate the Co and Fe before the analysis; (d) the error if the separation step is carried out; and (e) the maximum recovery for Fe if the recovery for Co is 1.00, and the maximum allowed error is 0.05%.
19. The amount of calcium in a sample of urine was determined by a method for which magnesium is an interferent. The selectivity coefficient, KCa,Mg, for the method is 0.843. When a sample with a Mg/Ca ratio of 0.50 was carried through the procedure, an error of –3.7% was obtained. The error was +5.5% when using a sample with a Mg/Ca ratio of 2.0. (a) Determine the recoveries for Ca and Mg. (b) What is the expected error for a urine sample in which the Mg/Ca ratio is 10.0?
20. Using the formation constants in Appendix 12, show that F– is an effective masking agent for preventing a reaction between Al3+ and EDTA. Assume that the only significant forms of fluoride and EDTA are F– and Y4-.
21. Cyanide is frequently used as a masking agent for metal ions. Its effectiveness as a masking agent is better in more basic solutions. Explain the reason for this pH dependency.
22. Explain how an aqueous sample consisting of Cu2+, Sn4+, Pb2+, and Zn2+ can be separated into its component parts by adjusting the pH of the solution.
23. A solute, S, has a distribution ratio between water and ether of 7.5. Calculate the extraction efficiency if you extract a 50.0-mL aqueous sample of S using 50.0 mL of ether as: (a) a single portion of 50.0 mL; (b) two portions, each of 25.0 mL; (c) four portions, each of 12.5 mL; and (d) five portions, each of 10.0 mL. Assume that the solute is not involved in any secondary equilibria.
24. What volume of ether is needed to extract 99.9% of the solute in problem 23 when using: (a) 1 extraction; (b) 2 extractions; (c) four extractions; and (d) five extractions.
25. What is the minimum distribution ratio if 99% of the solute in a 50.0-mL sample is to be extracted with a single 50.0-mL portion of an organic solvent? Repeat for the case where two 25.0-mL portions of the organic solvent are used.
26. A weak acid, HA, with a Ka of 1.0 × 10–5 has a partition coefficient, KD, of 1.2 × 103 between water and an organic solvent. What restriction on the sample’s pH is necessary to ensure that 99.9% of the weak acid in a 50.0-mL sample is extracted with a single 50.0-mL portion of the organic solvent?
27. For problem 26, how many extractions are needed if the sample’s pH cannot be decreased below 7.0?
28. A weak base, B, with a Kb of 1.0 × 10–3 has a partition coefficient, KD, of 5.0 × 102 between water and an organic solvent. What restriction on the sample’s pH is necessary to ensure that 99.9% of the weak base is in a 50.0-mL sample is extracted with two 25.0-mL portions of the organic solvent?
29. A sample contains a weak acid analyte, HA, and a weak acid interferent, HB. The acid dissociation constants and the partition coefficients for the weak acids are as follows: Ka,HA = 1.0 × 10–3, Ka,HB = 1.0 × 10–7, KD,HA = KD,HB = 5.0 × 102. (a) Calculate the extraction efficiency for HA and HB when a 50.0-mL sample, buffered to a pH of 7.0, is extracted with 50.0 mL of the organic solvent. (b) Which phase is enriched in the analyte? (c) What are the recoveries for the analyte and the interferent in this phase? (d) What is the separation factor? (e) A quantitative analysis is conducted on the phase enriched in analyte. What is the expected relative error if the selectivity coefficient, KHA,HB, is 0.500 and the initial ratio of HB/HA is 10.0?
30. The relevant equilibria for the extraction of I2 from an aqueous solution of KI into an organic phase are shown in Figure 7.32. (a) Is the extraction efficiency for I2 better at higher or at lower concentrations of I–? (b) Derive an expression for the distribution ratio for this extraction.
Figure 7.32 Extraction scheme for Problem 7.30.
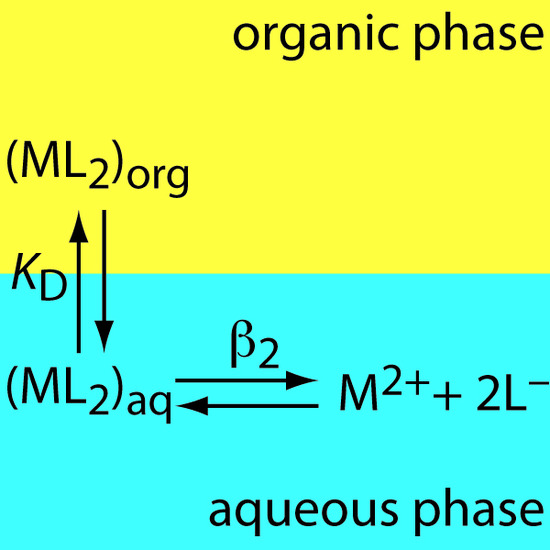
31. The relevant equilibria for extracting the metal-ligand complex ML2 from an aqueous solution into an organic phase are shown in Figure 7.31. (a) Derive an expression for the distribution ratio for this extraction. (b) Calculate the extraction efficiency when a 50.0-mL aqueous sample that is 0.15 mM in M2+ and 0.12 M in L– is extracted with 25.0 mL of the organic phase. Assume that KD is 10.3 and that β2 is 560.
Figure 7.33 Extraction scheme for Problem 7.31.
32. Derive equation 7.32.
33. The following information is available for the extraction of Cu2+ by CCl4 and dithizone: KD,c = 7 × 104; β2 = 5 × 1022; Ka,HL = 2 × 10–5;KD,HL = 1.01 × 104; and n = 2. What is the extraction efficiency if a 100-mL sample of an aqueous solution that is 1.0 × 10–7 M Cu2+ and 1 M in HCl is extracted with 10 mL of CCl4 containing 4.0 × 10–4 M dithizone (HL)?
34. Cupferron is a ligand whose strong affinity for metal ions makes it useful as a chelating agent in liquid–liquid extractions. The following table provides pH-dependent distribution ratios for the extraction of Hg2+, Pb2+, and Zn2+ from an aqueous solution to an organic solvent.
|
Distribution Ratio for |
|||
|
pH |
Hg2+ |
Pb2+ |
Zn2+ |
|
1 |
3.3 |
0.0 |
0.0 |
|
2 |
10.0 |
0.43 |
0.0 |
|
3 |
32.3 |
999 |
0.0 |
|
4 |
32.3 |
9999 |
0.0 |
|
5 |
19.0 |
9999 |
0.18 |
|
6 |
4.0 |
9999 |
0.33 |
|
7 |
1.0 |
9999 |
0.82 |
|
8 |
0.54 |
9999 |
1.50 |
|
9 |
0.15 |
9999 |
2.57 |
|
10 |
0.05 |
9999 |
2.57 |
(a) Suppose you have a 50.0-mL sample of an aqueous solution containing Hg2+, Pb2+, and Zn2+. Describe how you can effect a separation of these metal ions. (b) Under the conditions of your extraction for Hg2+, what percent of the Hg2+ remains in the aqueous phase after three 50.0-mL extractions with the organic solvent? (c) Under the conditions of your extraction for Pb2+, what is the minimum volume of organic solvent needed to extract 99.5% of the Pb2+ in a single extraction? (d) Under the conditions of your extraction for Zn2+, how many extractions are needed to remove 99.5% of the Zn2+ if each extraction uses 25.0 mL of organic solvent?
7.9.3 Solutions to Practice Exercises
Practice Exercise 7.1
To reduce the overall variance by improving the method’s standard deviation requires that
\[s^2=5.00\;\textrm{ppm}^2=s_\textrm{samp}^2+s_\textrm{meth}^2=(2.1\;\textrm{ppm})^2+s_\textrm{meth}^2\]
Solving for smeth gives its value as 0.768 ppm. Relative to its original value of 1.1 ppm, this is reduction of 3.0 × 101%. To reduce the overall variance by improving the standard deviation for sampling requires that
\[s^2=5.00\;\textrm{ppm}^2=s_\textrm{samp}^2+s_\textrm{meth}^2=s_\textrm{samp}^2+(1.1\;\textrm{ppm})^2\]
Solving for ssamp gives its value as 1.95 ppm. Relative to its original value of 2.1 ppm, this is reduction of 7.1%.
Click here to return to the chapter.
Practice Exercise 7.2
The analytical method’s standard deviation is 1.96 × 10–3 g/cm3 as this is the standard deviation for the analysis of a single sample of the polymer. The sampling variance is
\[s_\textrm{samp}^2=s^2-s_\textrm{meth}^2=(3.65\times10^{-2})^2-(1.96\times10^{-3})^2=1.33\times10^{-3}\]
Converting the variance to a standard deviation gives smeth as 3.64 × 10–2 g/cm3.
Click here to return to the chapter.
Practice Exercise 7.3
To determine the sampling constant, Ks, we need to know the average mass of the samples and the percent relative standard deviation for the concentration of olaquindox in the feed. The average mass for the five samples is 0.95792 g. The average concentration of olaquindox in the samples is 23.14 mg/kg with a standard deviation of 2.200 mg/kg. The percent relative standard deviation, R, is
\[R=\dfrac{s_\textrm{samp}}{\bar X}\times100=\mathrm{\dfrac{2.200\;mg/kg}{23.14\;mg/kg}\times100}=9.507\approx9.51\]
Solving for Ks gives its value as
\[K_\textrm s=mR^2=\mathrm{(0.95792\;g)(9.507)^2=86.58\;g\approx86.6\;g}\]
To obtain a percent relative standard deviation of 5.0%, individual samples need to have a mass of at least
\[m=\dfrac{K_\textrm s}{R^2}=\mathrm{\dfrac{86.58\;g}{(5.0)^2}=3.5\;g}\]
To reduce the sample’s mass from 3.5 g to 1 g, we must change the mass by a factor of
\[\mathrm{\dfrac{3.5\;g}{1\;g}=3.5\times}\]
If we assume that the sample’s particles are spherical, then we must reduce a particle’s radius by a factor of
\[r^3=3.5\times\]
\[r=1.5\times\]
Click here to return to the chapter.
Practice Exercise 7.4
Because the value of t depends on the number of samples—a result we have yet to calculate—we begin by letting nsamp = ∞ and using t(0.05, ∞) for the value of t. From Appendix 4, the value for t(0.05, ∞) is 1.960. Our first estimate for nsamp is
\[n_\textrm{samp}=\dfrac{t^2s_\textrm{samp}^2}{e^2}=\dfrac{(1.960)^2(5.0)^2}{(2.5)^2}=15.4\approx15\]
Letting nsamp = 15, the value of t(0.05, 14) from Appendix 4 is 2.145. Recalculating nsamp gives
\[n_\textrm{samp}=\dfrac{t^2s_\textrm{samp}^2}{e^2}=\dfrac{(2.145)^2(5.0)^2}{(2.5)^2}=18.4\approx18\]
Letting nsamp = 18, the value of t(0.05, 17) from Appendix 4 is 2.103. Recalculating nsamp gives
\[n_\textrm{samp}=\dfrac{t^2s_\textrm{samp}^2}{e^2}=\dfrac{(2.103)^2(5.0)^2}{(2.5)^2}=17.7\approx18\]
Because two successive calculations give the same value for nsamp, we need 18 samples to achieve a sampling error of ±2.5% at the 95% confidence interval.
Click here to return to the chapter.
Practice Exercise 7.5
If we collect a single sample (cost $20), then we can analyze that sample 13 times (cost $650) and stay within our budget. For this scenario, the percent relative error is
\[e=t \sqrt{\dfrac{s_\textrm{samp}^2}{n_\textrm{samp}}+\dfrac{s_\textrm{meth}^2} {n_\textrm{samp}n_\textrm{rep}}}=2.179\sqrt{\dfrac{0.10}{1}+\dfrac{0.20}{1\times13}}=0.74\]
where t(0.05, 12) is 2.179. Because this percent relative error is larger than ±0.50%, this is not a suitable sampling strategy.
Next, we try two samples (cost $40), analyzing each six times (cost $600). For this scenario, the percent relative error is
\[e=t \sqrt{\dfrac{s_\textrm{samp}^2}{n_\textrm{samp}}+\dfrac{s_\textrm{meth}^2} {n_\textrm{samp}n_\textrm{rep}}}=2.2035\sqrt{\dfrac{0.10}{2}+\dfrac{0.20}{2\times6}}=0.57\]
where t(0.05, 11) is 2.2035. Because this percent relative error is larger than ±0.50%, this also is not a suitable sampling strategy.
Next we try three samples (cost $60), analyzing each four times (cost $600). For this scenario, the percent relative error is
\[e=t \sqrt{\dfrac{s_\textrm{samp}^2}{n_\textrm{samp}}+\dfrac{s_\textrm{meth}^2} {n_\textrm{samp}n_\textrm{rep}}}=2.2035\sqrt{\dfrac{0.10}{3}+\dfrac{0.20}{3\times4}}=0.49\]
where t(0.05, 11) is 2.2035. Because both the total cost ($660) and the percent relative error meet our requirements, this is a suitable sampling strategy.
There are other suitable sampling strategies that meet both goals. The strategy requiring the least expense is to collect eight samples, analyzing each once for a total cost of $560 and a percent relative error of ±0.46%. Collecting 10 samples and analyzing each one time, gives a percent relative error of ±0.39% at a cost of $700.
Click here to return to the chapter.
Practice Exercise 7.6
The fluoride ion, F–, is a suitable masking agent as it binds with Al3+ to form the stable AlF63– complex, leaving iron in solution.
Click here to return to the chapter.
Practice Exercise 7.7
The relevant reactions and equilibrium constants are
\[\mathrm{Fe^{2+}}(aq)+\mathrm{3phen}(aq)\rightleftharpoons \mathrm{Fe(phen)_3^{2+}}(aq)\hspace{3mm}\beta_3=5\times10^{20}\]
\[\mathrm{Fe^{3+}}(aq)+\mathrm{3phen}(aq)\rightleftharpoons \mathrm{Fe(phen)_3^{3+}}(aq)\hspace{3mm}\beta_3=6\times10^{13}\]
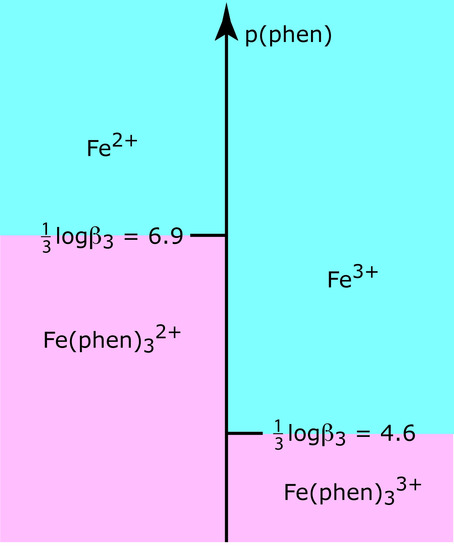
where phen is an abbreviation for 1,10-phenanthroline. Because β3 is larger for the complex with Fe2+ than it is for the complex with Fe3+, 1,10-phenanthroline will bind Fe2+ before it binds Fe3+. A ladder diagram for this system (Figure 6.34) suggests that an equilibrium p(phen) between 5.6 and 5.9 will fully complex Fe2+ without any significant formation of the Fe(phen)33+ complex. Adding a stoichiometrically equivalent amount of 1,10-phenanthroline to a solution of Fe2+ will be sufficient to mask Fe2+ in the presence of Fe3+. Adding a large excess of 1,10-phenanthroline, however, will decrease p(phen) and allow the formation of both metal–ligand complexes.
Figure 7.34 Ladder diagram for Practice Exercise 7.7.
Click here to return to the chapter.
Practice Exercise 7.8
(a) The solute’s distribution ratio between water and toluene is
\[D=\dfrac{[S_\textrm{org}]}{[S_\textrm{aq}]}=\mathrm{\dfrac{0.889\;g\times\dfrac{1\;mol}{117.3\;g}\times\dfrac{1}{0.00500\;L}}{(1.235\;g-0.889\;g)\times\dfrac{1\;mol}{117.3\;g}\times\dfrac{1}{0.01000\;L}}}=5.14\]
(b) The fraction of solute remaining in the aqueous phase after one extraction is
\[(q_\textrm{aq})_1=\dfrac{V_\textrm{aq}}{DV_\textrm{org}+V_\textrm{aq}}=\mathrm{\dfrac{20.00\;mL}{(5.14)(10.00\;mL)+20.00\;mL}}=0.280\]
The extraction efficiency, therefore, is 72.0%.
(c) To extract 99.9% of the solute requires
\[(Q_\textrm{aq})_n=0.001=\mathrm{\dfrac{20.00\;mL}{(5.14)(10.00\;mL)+20.00\;mL}}^n=0.280^n\]
\[\log(0.001)=n\log(0.280)\]
\[n=5.4\]
a minimum of six extractions.
Click here to return to the chapter.
Practice Exercise 7.9
Because the weak base exists in two forms, only one of which extracts into the organic phase, the partition coefficient, KD, and the distribution ratio, D, are not identical.
\[K_\textrm D=\mathrm{\dfrac{[B_{org}]}{[B_{aq}]}}\]
\[D=\mathrm{\dfrac{[B_{org}]_{total}}{[B_{aq}]_{total}}=\dfrac{[B_{org}]}{[B_{aq}]+[HB_{aq}^+]}}\]
Using the Kb expression for the weak base
\[K_\textrm b=\mathrm{\dfrac{[\ce{OH_{aq}^-}][HB^+_{aq}]}{[B_{aq}]}}\]
we solve for the concentration of HB+ and substitute back into the equation for D, obtaining
\[D=\mathrm{\dfrac{[B_{org}]}{[B_{aq}]+\dfrac{\mathit K_b\times[B_{aq}]}{[\ce{OH_{aq}^-}]}}=\dfrac{[B_{org}]}{[B_{aq}]1+\dfrac{\mathit K_b}{[\ce{OH_{aq}^-}]}}=\dfrac{\mathit K_D[\ce{OH_{aq}^-}]}{[\ce{OH_{aq}^-}]+\mathit K_b}}\]
At a pH of 9.0, the [OH−] is 1 × 10–5 M and the distribution ratio has a value of
\[D=\mathrm{\dfrac{\mathit{K_D}[\ce{OH_{aq}^-}]}{[\ce{OH_{aq}^-}]+\mathit{K_b}}}=\dfrac{(5.00)(1.0\times10^{-5})}{1.0\times10^{-5}+1.0\times10^{-4}}=0.455\]
After one extraction, the fraction of B remaining in the aqueous phase is
\[(q_\textrm{aq})_1=\mathrm{\dfrac{25.00\;mL}{(0.455)(50.00\;mL)+25.00\;mL}}=0.524\]
The extraction efficiency, therefore, is 47.6%. At a pH of 9, most of the weak base is present as HB+, which explains why the overall extraction efficiency is so poor.
Click here to return to the chapter.