Example Emphasized Terms

Introduction

So far, we have been analyzing compounds with a single chiral center. Next, we turn our attention to those which have multiple chiral centers. We'll start with some stereoisomeric four-carbon sugars with two chiral centers.

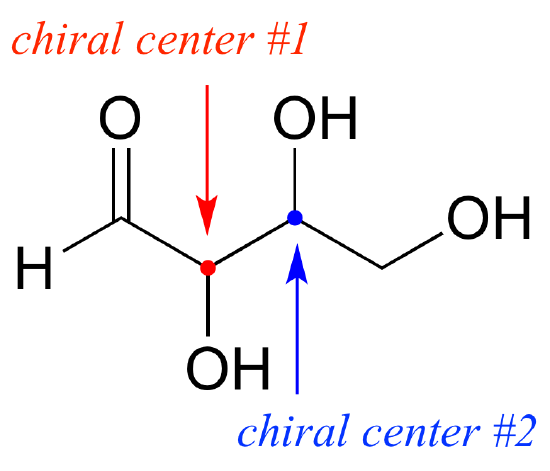
We will start with a common four-carbon sugar called D-erythrose.

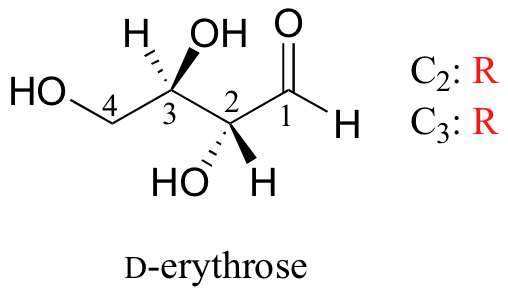
A note on sugar nomenclature: biochemists use a special system to refer to the stereochemistry of sugar molecules, employing names of historical origin in addition to the designators 'D' and 'L'. You will learn about this system if you take a biochemistry class. We will use the D/L designations here to refer to different sugars, but we won't worry about learning the system.

As you can see, D-erythrose is a chiral molecule: C₂ and C₃ are stereocenters, both of which have the R configuration. In addition, you should make a model to convince yourself that it is impossible to find a plane of symmetry through the molecule, regardless of the conformation. Does D-erythrose have an enantiomer? Of course it does – if it is a chiral molecule, it must. The enantiomer of erythrose is its mirror image, and is named L-erythrose (once again, you should use models to convince yourself that these mirror images of erythrose are not superimposable).

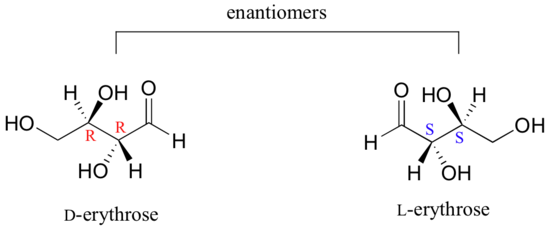
Notice that both chiral centers in L-erythrose both have the S configuration. To avoid confusion, we will simply refer to the different stereoisomers by capital letters.

Now let's consider all the possible stereoisomers

Look first at compound A below. Both chiral centers in have the R configuration (you should confirm this for yourself!). The mirror image of Compound A is compound B, which has the S configuration at both chiral centers. If we were to pick up compound A, flip it over and put it next to compound B, we would see that they are not superimposable (again, confirm this for yourself with your models!). A and B are nonsuperimposable mirror images: in other words, enantiomers.

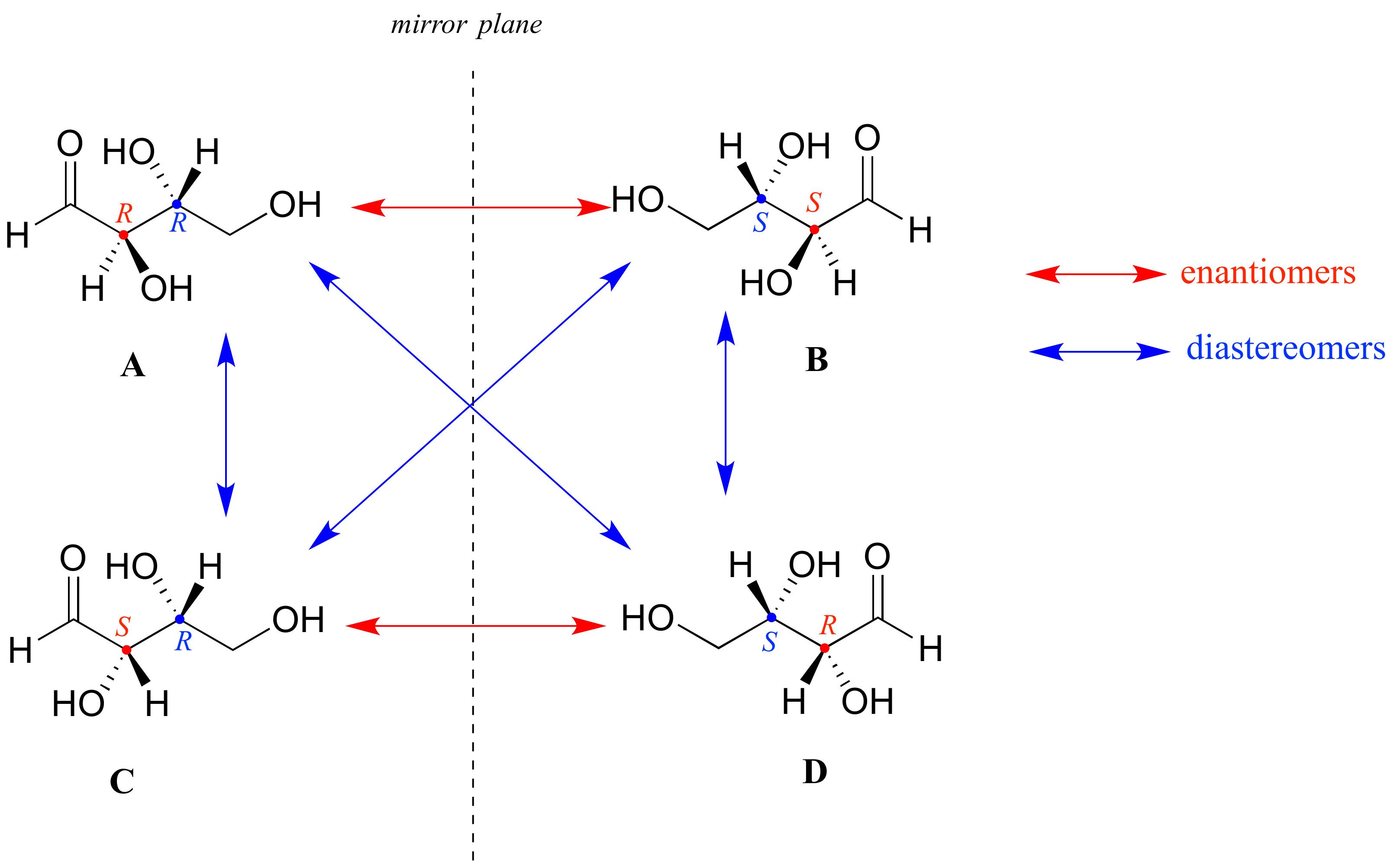
Now, look at compound C, in which the configuration is S at chiral center 1 and R at chiral center 2. Compounds A and C are stereoisomers: they have the same molecular formula and the same bond connectivity, but a different arrangement of atoms in space (recall that this is the definition of the term 'stereoisomer). However, they are not mirror images of each other (confirm this with your models!), and so they are not enantiomers. By definition, they are diastereomers of each other.

Notice that compounds C and B also have a diastereomeric relationship, by the same definition.

So, compounds A and B are a pair of enantiomers, and compound C is a diastereomer of both of them. Does compound C have its own enantiomer? Compound D is the mirror image of compound C, and the two are not superimposable. Therefore, C and D are a pair of enantiomers. Compound D is also a diastereomer of compounds A and B.

This can also seem very confusing at first, but there some simple shortcuts to analyzing stereoisomers:

Stereoisomer Shortcuts

If all of the chiral centers are of opposite R/S configuration between two stereoisomers, they are enantiomers.

If at least one, but not all of the chiral centers are opposite between two stereoisomers, they are diastereomers.

Here's another way of looking at the four stereoisomers, where one chiral center is associated with red and the other blue. Pairs of enantiomers are stacked together.

We know, using the shortcut above, that the enantiomer of RR must be SS - both chiral centers are different. We also know that RS and SR are diastereomers of RR, because in each case one - but not both - chiral centers are different.

Determining the Maximun Number of Stereoisomers for a Compound

In general, a structure with n stereocenters will have a maximum of 2ⁿ different stereoisomers. (We are not considering, for the time being, the stereochemistry of double bonds – that will come later). For example, let's consider the glucose molecule in its open-chain form (recall that many sugar molecules can exist in either an open-chain or a cyclic form). There are two enantiomers of glucose, called D-glucose and L-glucose. The D-enantiomer is the common sugar that our bodies use for energy. It has n = 4 stereocenters, so therefore there are 2ⁿ = 2⁴ = 16 possible stereoisomers (including D-glucose itself).

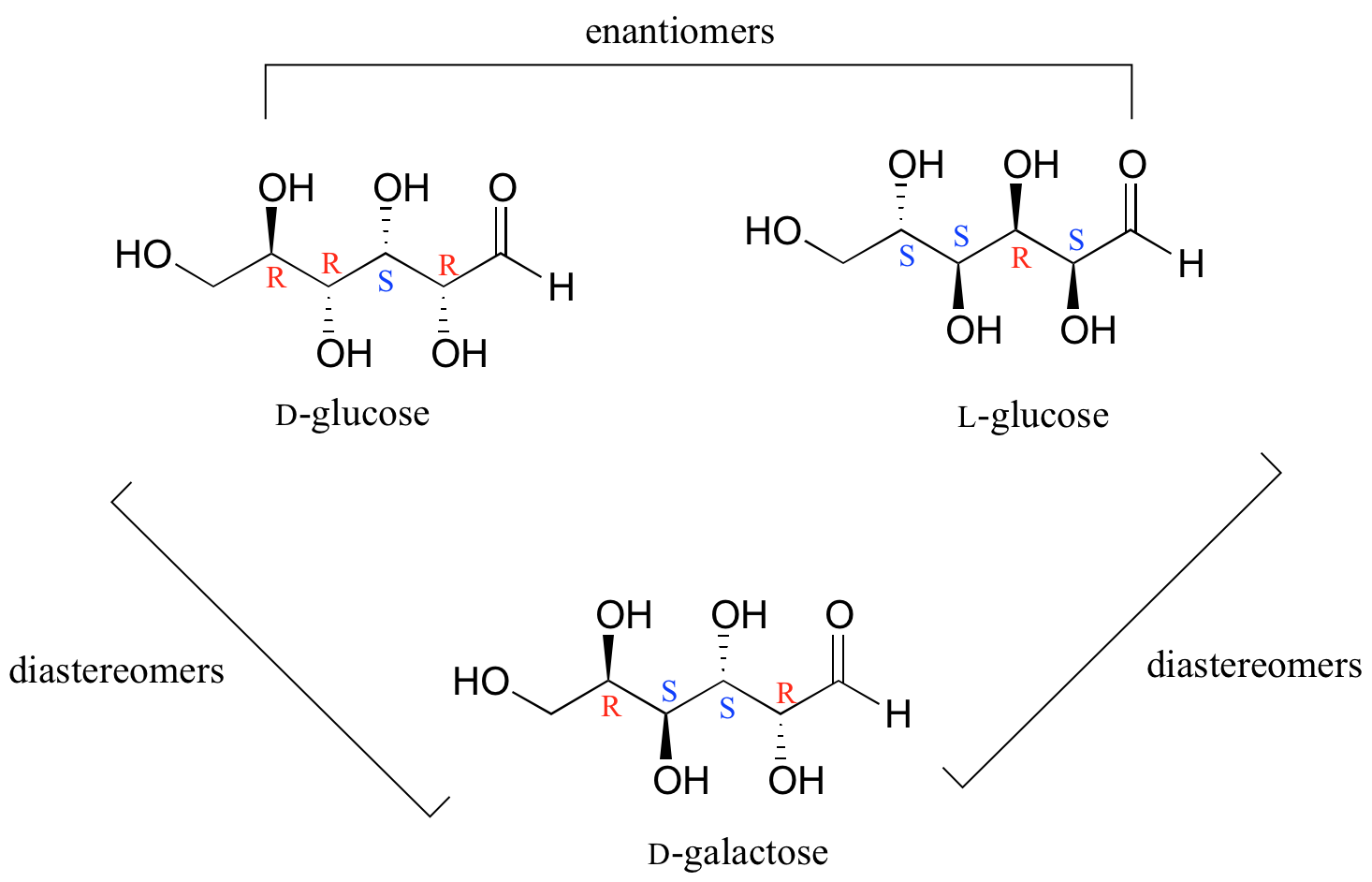
In L-glucose, all of the stereocenters are inverted relative to D-glucose. That leaves 14 diastereomers of D-glucose: these are molecules in which at least one, but not all, of the stereocenters are inverted relative to D-glucose. One of these 14 diastereomers, a sugar called D-galactose, is shown above: in D-galactose, one of four stereocenters is inverted relative to D-glucose. Diastereomers which differ in only one stereocenter (out of two or more) are called epimers. D-glucose and D-galactose can therefore be refered to as epimers as well as diastereomers.

Erythronolide B, a precursor to the 'macrocyclic' antibiotic erythromycin, has 10 stereocenters. It’s enantiomer is that molecule in which all 10 stereocenters are inverted.

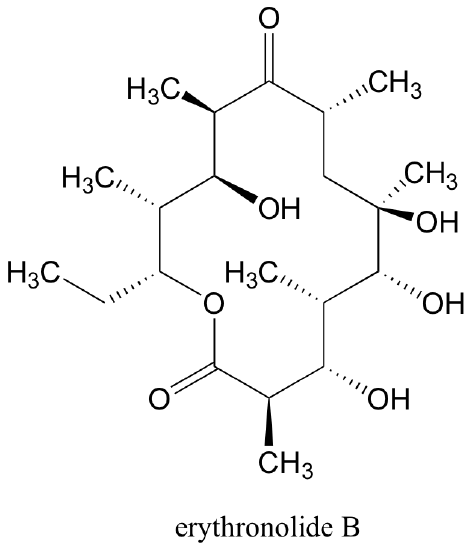
In total, there are 2¹⁰ = 1024 stereoisomers in the erythronolide B family: 1022 of these are diastereomers of the structure above, one is the enantiomer of the structure above, and the last is the structure above.

We know that enantiomers have identical physical properties and equal but opposite degrees of specific rotation. Diastereomers, in theory at least, have different physical properties – we stipulate ‘in theory’ because sometimes the physical properties of two or more diastereomers are so similar that it is very difficult to separate them. In addition, the specific rotations of diastereomers are unrelated – they could be the same sign or opposite signs, and similar in magnitude or very dissimilar.