Cyclic Monosaccharides
In Section 19-10 it was discussed that the reaction of one equivalent of an alcohol, in the presence of an acid catalyst, adds reversibly to aldehydes and ketones to form a hydroxy ether called a hemiacetal (R2COHOR') (hemi, Greek, half).

Molecules which have both an alcohol and a carbonyl can undergo an intramolecular version of the same reaction forming a cyclic hemiacetal.

Because sugars often contain alcohol and carbonyl functional groups, intramolecular hemiacetal formation is common in carbohydrate chemistry. Five and six-membered rings are favored over other ring sizes because of their low angle and eclipsing strain. Cyclic structures of this kind are termed furanose (five-membered) or pyranose (six-membered), reflecting the ring size relationship to the common heterocyclic compounds furan and pyran shown below.

Furan (5-membered ring) and pyran (6-membered ring) structures
Unlike most of the biochemical reactions you will see in this text, sugar cyclization reactions are not catalyzed by enzymes: they occur spontaneously and reversibly in aqueous solution. Sugars are often shown in their open-chain form, however, in aqueous solution, glucose, fructose, and other sugars of five or six carbons rapidly interconvert between straight-chain and cyclic forms. For most five- and six-carbon sugars, the cyclic forms predominate in equilibrium since they are more stable. The size of the cyclic hemiacetal ring adopted by a given sugar is not constant, but may vary with substituents and other structural features.
Aldohexoses usually form pyranose rings and their pentose homologs tend to prefer the furanose form, but there are many counter examples. At equilibrium less than 1% of glucose is in an open chain form with the rest being almost exclusively in its cyclic pyranose form. The pyranose ring is formed by attack of the hydroxyl on carbon 5 of glucose to the aldehyde carbon (carbon #1, also called the anomeric carbon in carbohydrate terminology). The cyclic form of glucose is called glucopyranose. Notice that for glucose and other aldohexoses the hydroxyl that forms the cyclic hemiacetal is also the one that determines the D/L designation of a sugar.
Pyranose rings are often drawn in a chair conformation like cyclohexane rings (Section 4-6) with substituents being either an axial or equatorial position. Pyranose rings are even capable of undergoing a ring flip to change between chair conformations. By convention the ring oxygen is placed to the right and to the rear of the structure (top right of the drawing). Groups which go to the right in a Fischer projection will be orientend 'down' of the pyranose ring while groups to the left are oriented 'up' in the chair structure. Also, the terminal -CH2OH group is oriented up on the pyranose ring for D-sugars and down for L-Sugars.
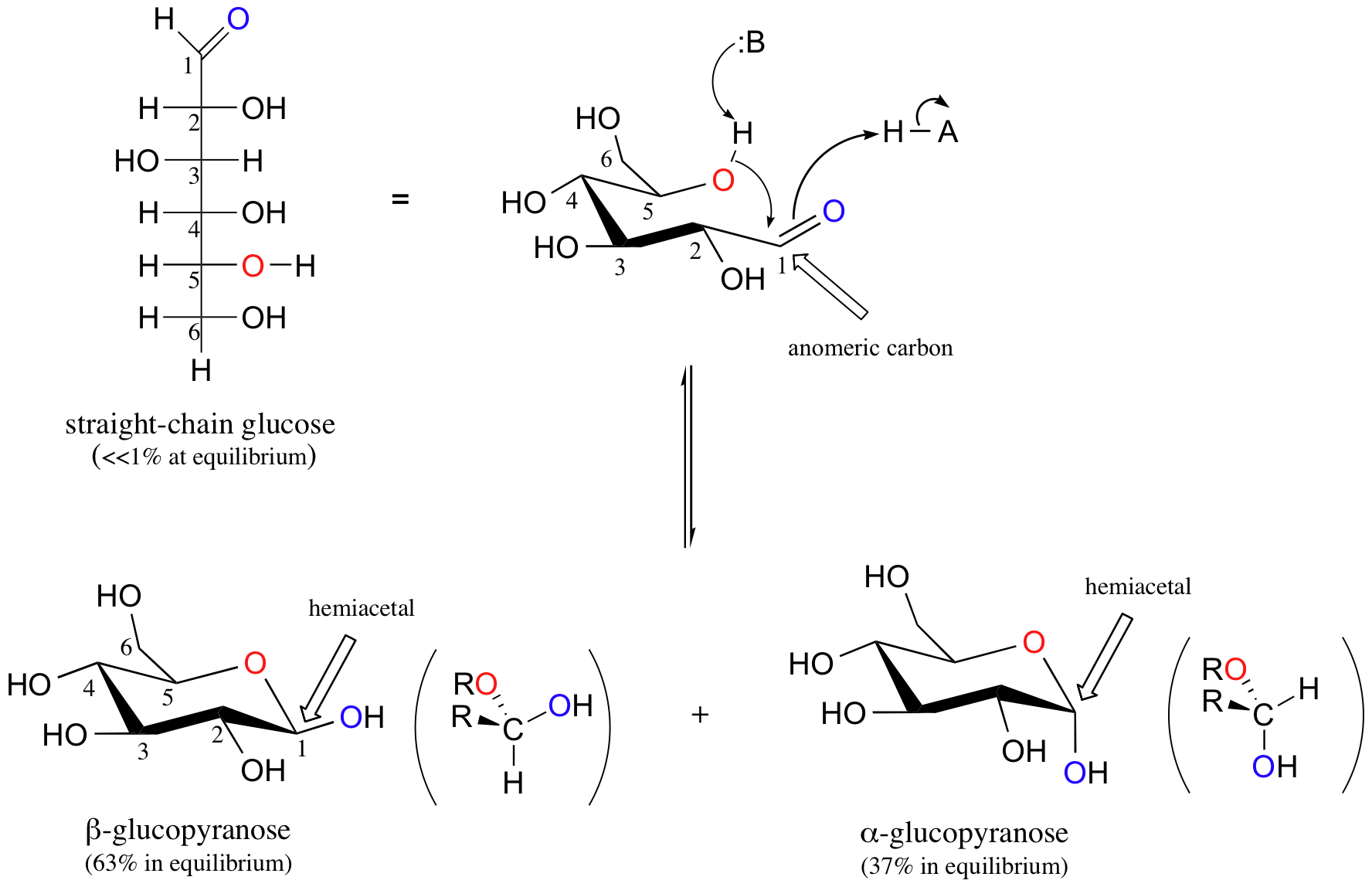
When D-glucose cyclizes it forms a 37/63 mixture of the alpha and beta anomer respectively. The beta anomer is preferred because β-D-glucopyranose is the only aldohexose which can be drawn with all its bulky substituents (-OH and -CH2OH) in equatorial positions, making it the most stable of the eight D-aldohexoses, which probably accounts for its widespread prevalence in nature.

It is possible to obtain a sample of crystalline glucose in which all the molecules have the α structure or all have the β structure. The α form melts at 146°C and has a specific rotation of +112°, while the β form melts at 150°C and has a specific rotation of +18.7°. When the sample is dissolved in water, however, a mixture is soon produced containing both anomers as well as the straight-chain form, in dynamic equilibrium. You can start with a pure crystalline sample of glucose consisting entirely of either anomer, but as soon as the molecules dissolve in water, they open to form the carbonyl group and then re-close to form either the α or the β anomer. The opening and closing repeats continuously in an ongoing interconversion between anomeric forms and is referred to as mutarotation (Latin mutare, meaning “to change”). At equilibrium, the mixture consists of about 36% α-D-glucose, 64% β-D-glucose, and less than 0.02% of the open-chain aldehyde form. The observed rotation of this solution is +52.7°.
Example \(\PageIndex{1}\)
-
Fructose in aqueous solution forms a six-membered cyclic hemiketal called fructopyranose when the hydroxyl oxygen on carbon #6 attacks the ketone carbon (carbon #2, the anomeric carbon in fructose).
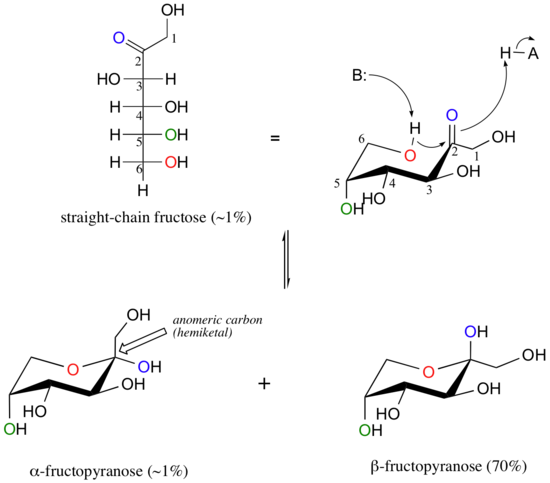
In this case, the β anomer is heavily favored in equilibrium by a ratio of 70:1, because in the minor α anomer the bulkier -CH2OH group occupies an axial position. Notice in the above figure that the percentages of α and β anomers present at equilibrium do not add up to 100%. Fructose also exists in solution as a five-membered cyclic hemiketal, referred to in carbohydrate nomenclature as fructofuranose. In the formation of fructofuranose from open-chain fructose, the hydroxyl group on the fifth carbon attacks the ketone.

In aqueous solution, then, fructose exists as an equilibrium mixture of 70% β-fructopyranose, 23% β-fructofuranose, and smaller percentages of the open chain and cyclic α-anomers. The β-pyranose form of fructose is one of the sweetest compounds known, and is the main component of high-fructose corn syrup. The β-furanose form is much less sweet.
Although we have been looking at specific examples for glucose and fructose, other five- and six-carbon monosaccharides also exist in solution as equilibrium mixtures of open chains and cyclic hemiacetals and hemiketals. Shorter monosaccharides are unlikely to undergo analogous ring-forming reactions, however, due to the inherent instability of three and four-membered rings.
Drawing Cyclic Structures of Monosaccharides
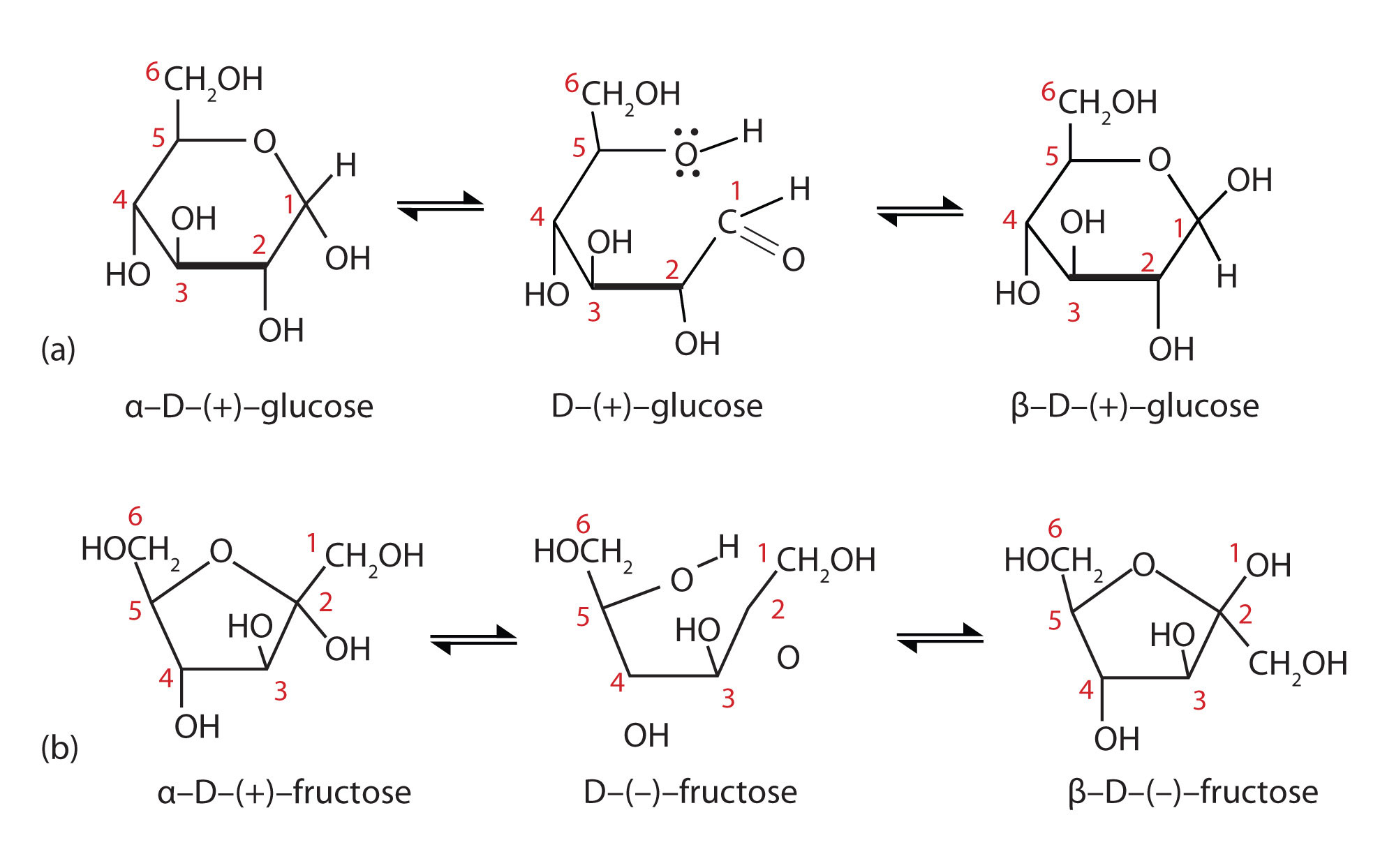
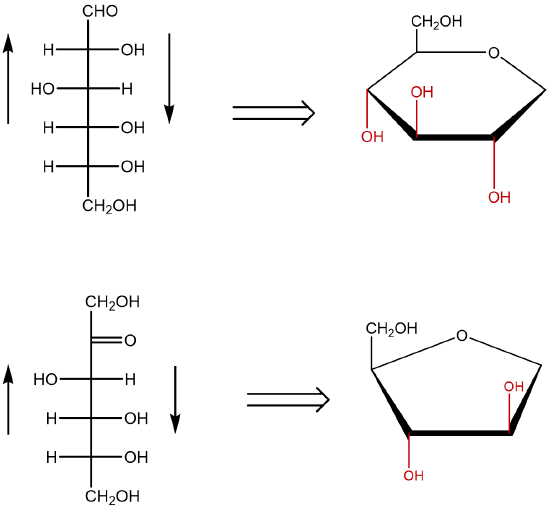
The cyclic forms of sugars are commonly depicted as Haworth projections. This convention, first suggested by the English chemist Walter N. Haworth, shows molecules drawn as planar rings with darkened edges representing the side facing toward the viewer. The structure is simplified to show only the functional groups attached to the carbon atoms. Any group written to the right in a Fischer projection appears below (bottom face) the plane of the ring in a Haworth projection, and any group written to the left in a Fischer projection appears above (top face) the plane in a Haworth projection.

Figure: Conversion of the Fischer projection of D-glucose to the Haworth projection of ß-D-glucose.
- When converting a Fischer projection (line) to a Haworth projection, you must first identify the type of monosaccharide involved. If the carbohydrate represents an aldohexose, the pyranose ring is typically used. A pyranose is a cyclic structure that contains five carbon atoms and an oxygen. If the carbohydrate represents a ketohexose, the furanose ring is typically used. The furanose ring contains four carbon atoms and an oxygen.
.png?revision=1&size=bestfit&width=412&height=201)
- Indicate the arrangement of the hydroxyl group attached to the anomeric carbon to identify the sugar as an alpha or beta anomer. The α and β anomers are determined with respect to carbon 6. If the molecule represents a D-sugar, carbon 6 will be above the plane of the ring (top face) and form an L-sugar, carbon 6 will be below the plane of the ring (ring). The α anomer occurs when the OH on the anomeric carbon is trans to carbon 6 and the β anomer occurs when the OH on the anomeric carbon is cis to carbon 6. If the cyclic structure contains a furanose, since carbon 1 is not included within the ring, that carbon group would be arranged in the opposite direction of the OH group.
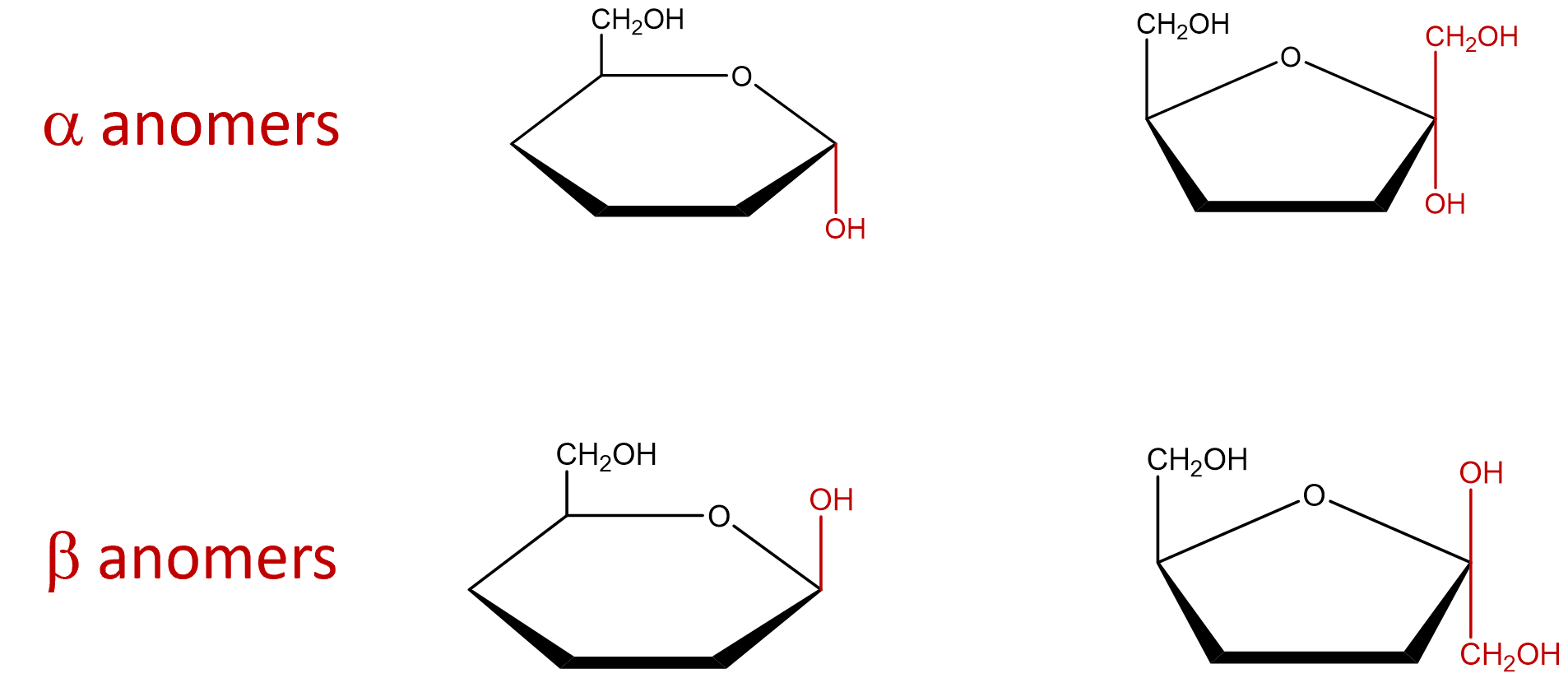
- The remaining chiral centers (carbons 2, 3 and 4 of the pyranose or carbons 3 and 4 of the furanose) are arranged based on the directions of the hydroxyl from the Fischer projection structures. Groups to the left of the Fischer projection would point up (top face), while groups to the right would point down (bottom face).
Since the Fischer Projection of any given carbohydrate is always the same, the Haworth Projection is essentially always the same. The only differences between the Haworth Projection of the alpha or beta form of a single carbohydrate, is how the OH (and carbon 1 if furanose ring) is arranged around the anomeric carbon to determine whether the molecule is alpha or beta.
.png?revision=1&size=bestfit&width=480&height=461)
Previously, we have seen the six ring atoms of cyclic glucose drawn in two dimensions. A more accurate depiction shows that the molecule adopts, as expected, a chair conformation.
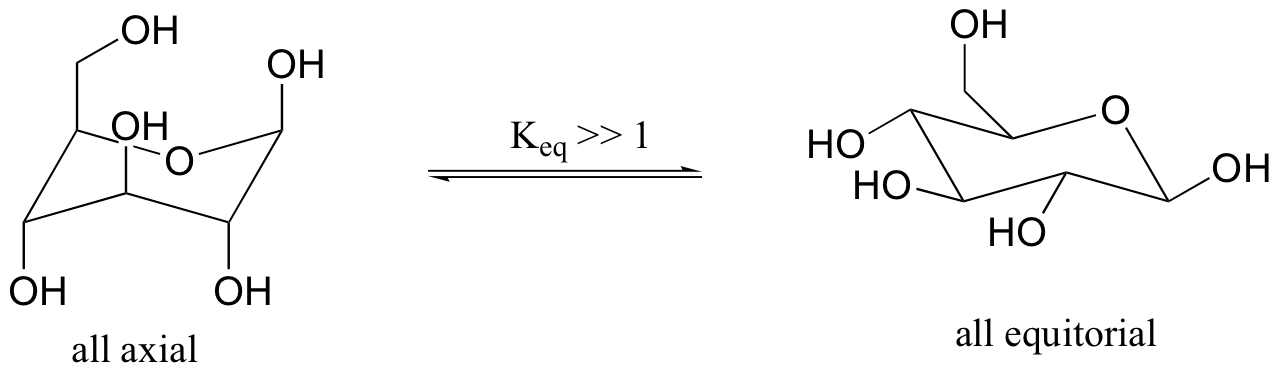
The conformation in which all substituents are equatorial is lower in energy. The two isomeric forms are referred to by the Greek letters alpha (α) and beta (β).

We have not learned about stereoisomerism quite yet, but you can still recognize that the bonding configuration on one carbon is different. On the alpha isomer, one of the hydroxyl groups is axial – this isomer is not able to adopt a chair conformation in which all non-hydrogen substituents are equatorial. The lower energy conformation is the one in which four of the five substituents are equatorial, but the presence of the one axial hydroxyl group means that the alpha isomer is, overall, less stable than the beta isomer.
The most abundant form of fructose in aqueous solution is also a six-membered ring.

The lower energy chair conformation is the one with three of the five substituents (including the bulky –CH2OH group) in the equatorial position.
Exercise \(\PageIndex{1}\)
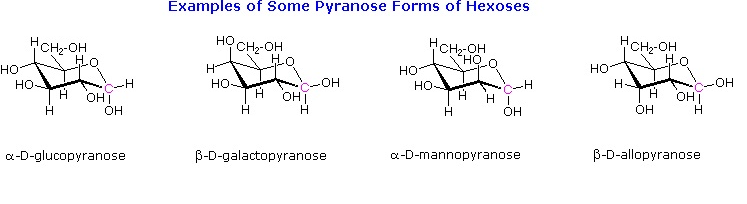
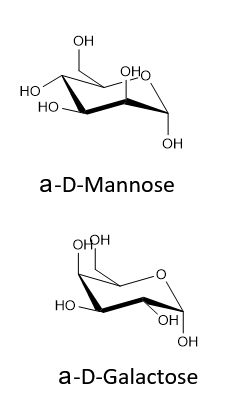
Draw the following in their most stable chair conformation: α-D-galactopyranose and α-D-mannopyranose. Which is expected to be the more stable?
- Answer
-
Because the both have two axial OH's their chair conformations should be roughly the same stability.
Exercise \(\PageIndex{2}\)
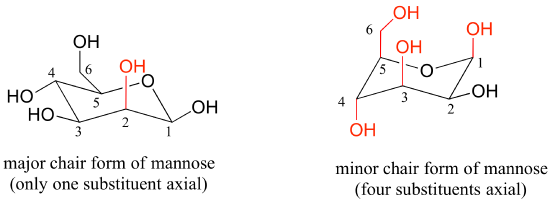
Draw the two chair conformations of the sugar called mannose, being sure to clearly show each non-hydrogen substituent as axial or equatorial. Predict which conformation is likely to be more stable, and explain why.

- Answer
-
Exercise \(\PageIndex{3}\)
Draw the cyclic structure of α-D-altrose.
- Answer
-

Exercise \(\PageIndex{4}\)
Draw the cyclic structure for β-D-galactose. Identify the anomeric carbon.
- Answer
-
.png?revision=1&size=bestfit&width=288&height=163)
To identify the structure, we should first start with the Fischer projection of D-galactose. Since it is an aldohexose, we will start with the pyranose ring. The beta anomer was requested, so the OH on the anomeric carbon (C1) is cis to C6. Since C6 is top face (pointing up), the OH will be top face. Carbons 2, 3, and 4 are then arranged based on the Fischer projection arrangement at those carbons (C2 right, C3 left, and C4 left).
Exercise \(\PageIndex{5}\)
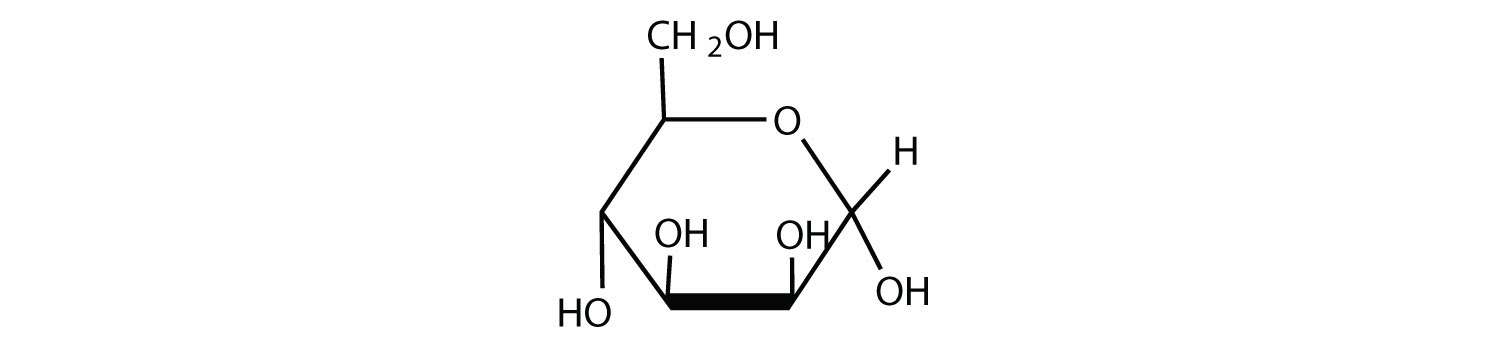
Given that the aldohexose D-mannose differs from D-glucose only in the configuration at the second carbon atom, draw the cyclic structure for α-D-mannose.
- Answer
-
Exercise \(\PageIndex{6}\)
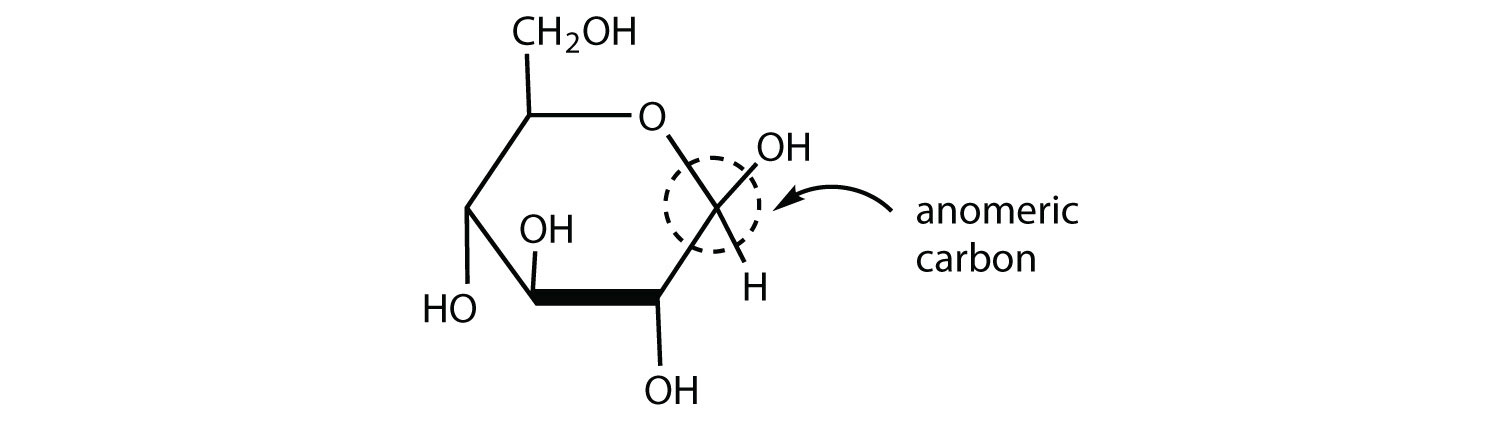
Draw the cyclic structure for β-D-glucose. Identify the anomeric carbon.
- Answer
-
Exercise \(\PageIndex{7}\)
a) Identify the anomeric carbon of each of the sugars shown below, and specify whether the structure shown is a hemiacetal or hemiketal.
b) Draw mechanisms for cyclization of the open-chain forms to the cyclic forms shown.

- Answer
-

Exercise \(\PageIndex{8}\)
Draw a mechanism for the conversion of α-glucopyranose to open-chain glucose.
- Answer
-

6.
Exercise \(\PageIndex{9}\)
Identify the following monosaccharide, write its full name, and draw its open-chain form as a Fischer projection.
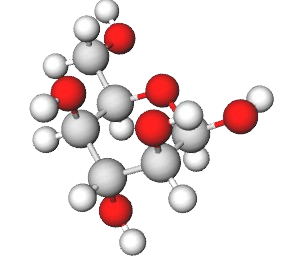
- Answer
-
β-D-idopyranose.








.png?revision=1&size=bestfit&width=412&height=201)


.png?revision=1&size=bestfit&width=480&height=461)
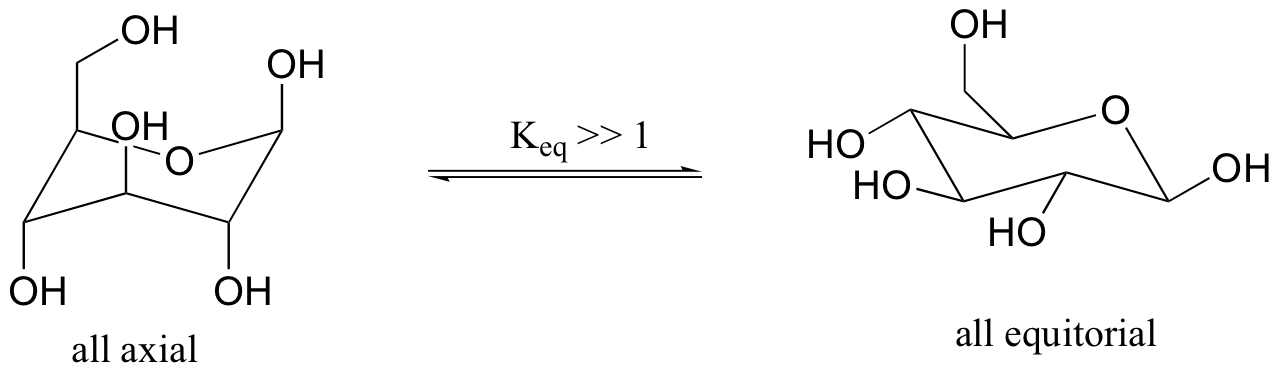






.png?revision=1&size=bestfit&width=288&height=163)





