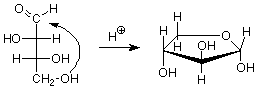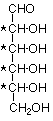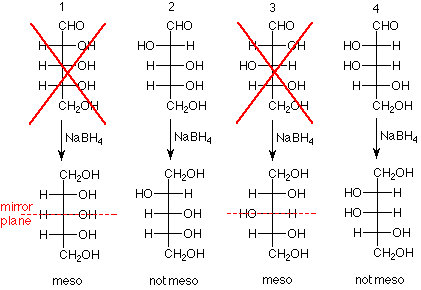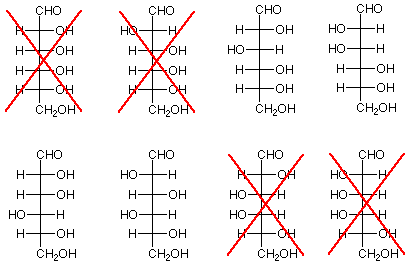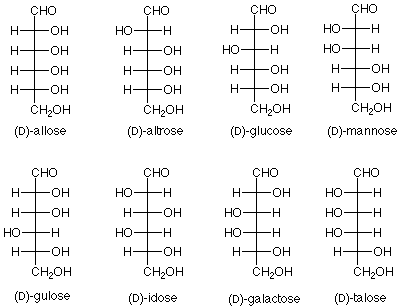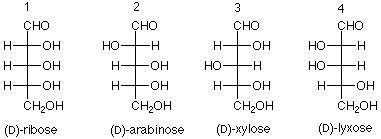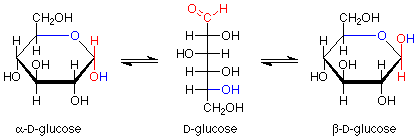14.2: Carbohydrates- Monosaccharides

Mono-, Di-, and Polysaccharides

Sugars are small molecules which belong to the class of carbohydrates. As the name implies, a carbohydrate is a molecule whose molecular formula can be expressed in terms of just carbon and water. For example, glucose has the formula C₆(H₂O)₆ and sucrose (table sugar) has the formula C₆(H₂O)₁₁. More complex carbohydrates such as starch and cellulose are polymers of glucose. Their formulas can be be expressed as C_n(H₂O)_n-1. We'll look at them in more detail next time.

The difference between a monosaccharide and a disaccharide can be seen in the following example:

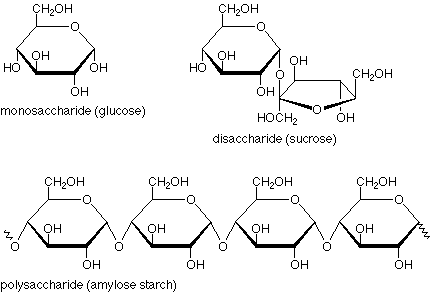
A quick glance tells us that a monosaccharide has just one ring, a disaccharide has two, and a polysaccharide has many. Beyond that, though, there's another important structural feature. Look at the disaccharide and focus on the oxygen which links the two rings together. The atom above it is connected to two oxygens, both of which are in ether-type situations. The carbon and these oxygens are in an acetal linkage. (The bonds are heavier and in blue.)

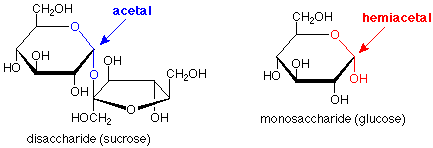
If we look at the corresponding location in the monosaccharide and ask what the functional group might be, we see that it is a hemiacetal. (Here the bonds are heavier and in red.) So, another way to describe the situation is that a monosaccharide has a single ring with a hemiacetal in it, a disaccharide has two rings linked by an acetal functional group, and a polysaccharide has many rings linked by many acetal functional groups. (Check this last statement against the polysaccharide structure above).

How about the "sugars" we saw last time with just 4 carbons. Why are they monosaccharides when there is no ring? If we consider that the OH group on the bottom carbon could form a hemiacetal with the aldehyde function, then we get a ring, and that structure fits our description of a monosaccharide.

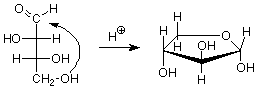
We'll take a more detailed look at the cyclic and non-cyclic structures of sugars shortly.

"Oses" and D-Sugars

Now let's see what aldotetrose means. Taking the name apart from right to left, the ending "ose" means a sugar, which may be a monosaccharide, a disaccharide or an oligosaccharide (a "short" polysaccharide). The middle part "tetr" means that our sugar has four carbons linked in a straight unbranched chain. Terms like "pent" for five carbons and "hex" for six carbons are also in common use. The beginning "aldo" means that there is an aldehyde in the compound. The alternative would be a ketone group, for which we would use the prefix "keto."

Glucose, the most common monosaccharide, is an aldohexose. We understand that to mean that it is a sugar having six carbons in a straight unbranched chain which ends in an aldehyde group. We can represent that structure in this fashion:

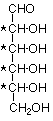
This structure includes four stereogenic carbon atoms (marked with an asterisk *). There are a total of sixteen stereoisomers possible. Eight of these are enantiomers of the other eight. The rest of the relationships are diastereoisomeric. Since the groups at the top and the bottom of the chain are not the same, there are no meso isomers. Eight of the isomers are shown here. The other eight are mirror images of these and may be readily drawn.

The question is "which of the sixteen stereochemical representations (Fischer projections, remember that each stereoisomer shown also has an enantiomer which is not shown) describes the absolute configuration of glucose? When Emil Fischer took up this problem about 100 years ago, he realized that there was no way to determine if glucose was one of the eight structures above or one of the unshown enantiomers. He made the assumption that it was one of the ones above so that he could work on the diastereoisomeric part of the problem, hoping that later work would resolve the question of which enantiomer best represented glucose.

Fischer also developed the D/L system for specifying the structures of sugars. If the OH group on the stereogenic carbon farthest from the aldehyde group is to the right in the Fischer projection, then the compound is a D-sugar. All of the sugars in the figure above are D-sugars. If the OH group on the stereogenic carbon farthest from the aldehyde group is to the left in the Fischer projection, then the compound is an L sugar. The enantiomers of all the sugars in the figure above are L sugars. Fischer's assumption amounts to saying that glucose is a D-sugar. Later work resolved this issue, and Fischer was right.

Which D-aldohexose is Glucose?

How did Fischer determine which of the eight structures above was glucose? He had available samples of glucose and mannose, both aldohexoses, and arabinose, an aldopentose. He also learned how to reduce the aldehyde functional group to a primary alcohol. (We'll illustrate this with NaBH₄ to avoid learning a new reaction, but he used another reagent.) He developed a method for extending the carbon chain of an aldose (called the Kiliani-Fischer chain extension). He also had a polarimeter so he could determine whether a sample was optically active or not. Perhaps most importantly, he had a group of talented and dedicated students.

Now, some data.

Experimental result: When the aldehyde group of arabinose was reduced to a primary alcohol group, the product was optically active.

Conclusion: Arabinose has either structure 2 or 4 in the scheme below. This is because if arabinose were either 1 or 3, the product would have a plane of symmetry (mirror plane) and would be optically inactive.

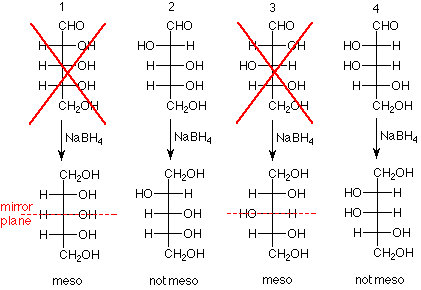
Experimental result: When the aldehyde group of glucose was reduced to a primary alcohol group, the product was optically active. The same result was obtained for mannose.

Conclusion: The structures "X'd" out below do not represent either glucose or mannose since the products from these structures would be meso compounds.

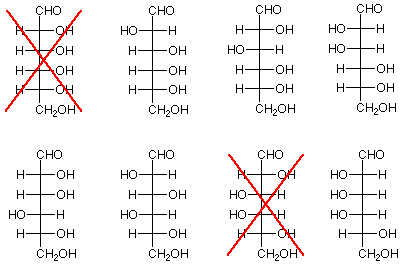
Experimental result: Kiliani-Fischer chain extension applied to arabinose produces glucose and mannose.

Conclusion: The bottom three stereogenic carbon atoms of glucose and mannose are have identical configurations to the three stereogenic carbon atoms of arabinose. This means that glucose and mannose differ only in the configuration of the stereogenic carbon atom nearest the aldehyde functional group. We can further conclude that if one member of a pair of aldohexoses (paired because their bottom three stereogenic carbons are identical) is ruled out, so is the other

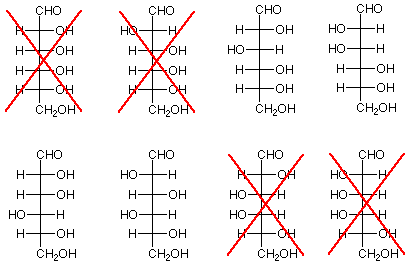
Now let's see what we have left. There are four structures remaining as candidates. They are on the right below. If we go back to the possibilities for arabinose, we find that the two on the top come from structure 2 for arabinose, which was a possibility, while the two on the bottom come from structure 3, which was ruled out earlier. The conclusion is that arabinose is represented by structure 2, and glucose and mannose are the two structures to its right.

But which is glucose and which is mannose? Fischer noticed that if reactions could be developed which changed the aldehyde group into a primary alcohol and the primary alcohol into an aldehyde (switch ends) one of these structures would give itself, and the other would give back a new L sugar. The reactions are complex and we will not look at them, but when the chemistry was applied to the sample called mannose, the product was mannose. When the chemistry was applied to the sample called glucose, a new sugar was formed.

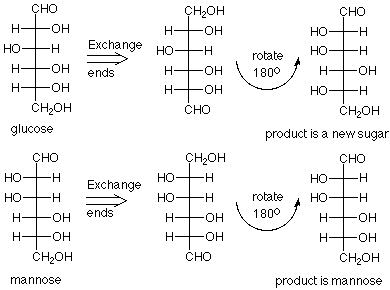
There was a great deal more to be done to confirm this conclusion and to synthesize the other six aldohexoses, but Fischer's exercise in logic and dedicated experimentation led to the conclusion that the eight D-aldohexoses are:

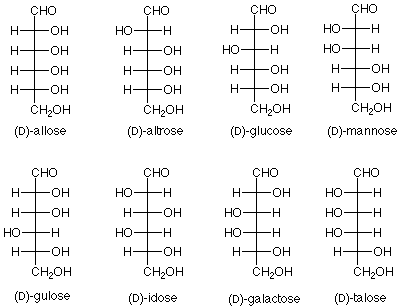
Notice that the new sugar which was produced from glucose by the "exchange ends" experiment is L-gulose. The names of the hexoses tell us which diastereoisomer we have; the D or L designation gives us which enantiomer we have.

The corresponding names for the aldopentoses are:

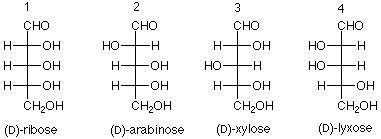
Cyclic Structures - Anomers

To finish today, we'll see what happens when a hemiacetal is formed between the aldehyde carbon and one of the OH groups on the chain. We'll look at two examples, ribose, which is a key component of RNA, and glucose because of its abundance. (You may wish to review the mechanism for hemiacetal formation.)

Since there are four OH groups in ribose, we could anticipate four different ring sizes. In three atom rings and four atom rings the bond angles are far from 109.5^o, so these rings are strained, have higher energies and are hard to form. Remember that there is an equilibrium between a hemiacetal and the aldehyde/alcohol it comes from, and that high energy materials don't persist at equilibrium. We are left with rings which have either five or six atoms in them. In the case of ribose the important ring (found in RNA) is the five membered ring.

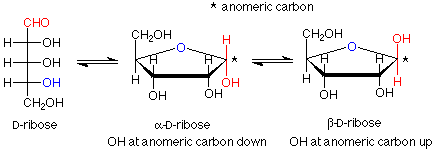
Notice that the carbon in the newly formed hemiacetal group is stereogenic. This means that there are two possible diastereoisomers for the cyclic structure. Usually both are formed, and they have a special name -- they are anomers of each other. The carbon between the two oxygens in the hemiacetal group is called the anomeric carbon. If the OH group is down (in a drawing with the ring oxygen to the rear center or right), the designation for that anomer is alpha. If the OH group is up, the designation is beta. Since the alpha and beta anomers are diastereoisomers, they have different properties; in particular, different optical activities. The term for a five atom sugar ring is "furanose."

Glucose usually makes hemiacetal cyclic structures with six atom rings, although five membered rings can also be formed when the six membered rings are precluded. Such six membered rings are named by the term "pyranose." The ring forms look like this, keeping in mind that alpha and beta anomers are also involved here:

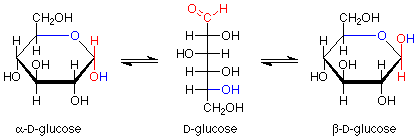
Again, we have an equilibrium between the open chain form and the two diastereoisomeric anomers.

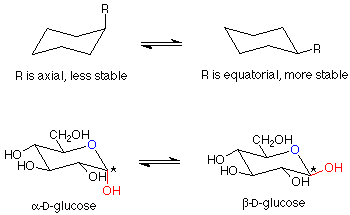
There is one further point to be made about these glucopyranoses. The structure we have drawn for the ring is flat. The bond angles would be 120^o, quite far from the normal tetrahedral value of 109.5^o. The atoms in the ring can have bond angles of about 109.5^o if the ring puckers as shown here:

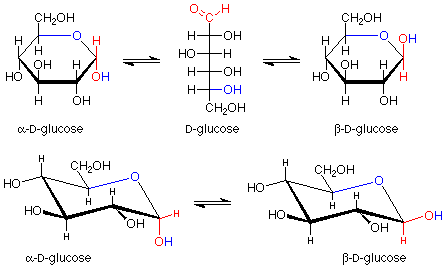
Of course, molecules adopt these puckered shapes (called chair conformations from their resemblance to a rather wide lounge chair) automatically. You can review the material on cyclohexane for a more detailed analysis of this material. It has been established that in these chair conformations, the molecules have a lower energy if the larger substituents on the carbons are roughly in the plane of the ring itself. These positions are called "equatorial" to distinguish them from the other positions (roughly perpendicular to the ring, called "axial"). A compound which can have all of its larger substituents (everything is larger than hydrogen) in an equatorial position is more stable than one which cannot. beta-D-glucose has all of its substituents in equatorial positions, and is thus the most stable hexopyranose. It is also the most abundant.