Molecular modeling - Computational chemistry

Introduction

The general theory of quantum mechanics is now almost complete… The underlying physical laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known, and the difficulty is only that exact application of these laws leads to equations much too complicated to be soluble. It therefore becomes desirable that approximate practical methods of applying quantum mechanics should be developed.

—P. A. M. Dirac, 1929

An Introduction to Computational Chemistry

The quantum mechanical calculations utilized in this exercise are beyond the scope of General Chemistry as the concepts require a thorough understanding of calculus and differential equations. If you are interested, these topics are covered in Physical Chemistry. That being said, a general idea of inner workings (excluding as much complex math as possible) will be detailed herein.

Quantum chemistry is centered on the Schrödinger equation:

EΨ = ĤΨ [1]

, where Ψ is the wavefunction, E is the energy of the system, and Ĥ is the Hamiltonian operator.

You might be asking yourself, “What is this wavefunction thing?” A wavefunction is a mathematical function to describe the wave-like behavior of an electron. The wavefunction itself does not describe anything physical, but if you multiply the wavefunction by its complex conjugate (Ψ^*):

Ψ^*Ψ = |Ψ²| [2]

, then you get the electron probability density (ρ), which is an observable property. However, the Schrödinger equation can currently only be solved exactly for one electron systems, such as the hydrogen atom. So what good is this model if we can only look at one electron systems? The answer is not much, so we need to make additional approximations to move beyond one electron systems.

An example of one of these approximations is the Linear Combinations of Atomic Orbitals (LCAO). In this approximation, basis functions (φ) are used in the construction of molecular orbitals (MOs). MOs are used to describe the electronic structure of a molecule whereas atomic orbitals (AOs) describe the electronic structure of an atom. The mathematical form of the LCAO approximation is given by:

\(\psi_{mo} = \ \sum_{}^{}{{\ c}_{i\ }\varphi}_{i}\) [3]

,where \(\psi_{mo}\) is the wavefunction of the molecular orbital, φ_i represents the atomic orbital wavefunctions, and the c_i terms are the “percentages” for each atomic orbital. In an H₂ molecule, the form of the σ bonding MO would look like the following:

ψ₊=  c_a φ_a+  c_b φ_b [4]

, where φ_a is the atomic orbital on “hydrogen a”, φ_b is the atomic orbital on “hydrogen b”, and c_a/c_b are the contributions of atomic orbitals to the overall MO. If we use a minimal basis set then we know that the atomic orbitals for each hydrogen can be represented by a 1s orbital, and the fact that each AO of the hydrogen contributes equally in this so-called pure covalent system, then the H₂ σ bonding MO could be expressed by:

\(\psi_{+} = \ {\frac{1}{\sqrt{2}}\lbrack\varphi}_{a,1s} + \ \varphi_{b,1s}\rbrack\) [5]

Depending on the approximations made one arrives at different ways to model quantum chemical systems. Despite the large number of approximations that go into these different models, they can get within “chemical accuracy” if properly used. Some approximations include Hartree-Fock (HF) Theory, Density Functional Theory (DFT), Møller-Plesset (MP) models, Coupled-Cluster (CC), and configuration interaction (CI). Each model has its limitations and users should be aware of those limitations.

Some terminology:

Level of Theory – This is the theoretical model selected for the calculation. This includes HF, DFT, etc.

Basis Sets/Functions – A basis set is a mathematical function used in the construction of the molecular orbitals.

Practical quantum chemistry (what an oxymoron, right?) is a balance between calculation accuracy and computational expense (time). A quality quantum chemist selects the level of theory, along with the basis sets, to get a reasonable result in a reasonable amount of time. Additionally, knowing the “meaningful” digits from the results of these calculations is important.[4]

In this exercise you will be conducting quantum chemical calculations to make predictions about macroscopic properties, such as miscibility.

References:

[1] Engel, T.; Reid, P. Physical Chemistry, 3^rd Edition. Pearson: Boston, 2013.

[2] Cooksy, A. Physical Chemistry Quantum Chemistry and Molecular Interactions. Pearson: Boston, 2014.

[3] Levine, I.N. Quantum Chemistry, 7^th Ed. Pearson: Boston, 2014.

[4] Hoffmann, R.; Schleyer, P.R.; Schaefer, H.F. Predicting Molecules-More Realism, Please. Angew. Chem. Int. Ed., 2008, 47, 7164-7167. 

Procedure

Part 1 – Which is the lowest-energy structure?

You will use the free version of WebMO, a web-based interface to perform quantum chemical calculations to investigate the energy and the equilibrium geometry of hypochlorous acid (HClO) to confirm which geometry is the lowest in energy structure. You’ll consider the calculated “heat of formation,” or the amount of heat that is either absorbed or released as the molecule forms from its elements. If the heat of formation is negative, then heat is released. If the heat of formation is positive, then heat is absorbed. The isomer that has a lower heat of formation (more negative) will be energetically favored and more stable than the isomer with higher heats of formation.

Computational Procedure:

You will use the program to determine the best geometry for each molecule (the best geometry will produce a minimum in the heat of formation). After drawing the VSEPR model for the isomers of hypochlorous acid on the summary sheet, continue with the procedure below.

You can use the “WebMO” app on your smart phone for this computational experiment.

1. You will be “drawing” a representation of the HOCl molecule in the WebMO app.

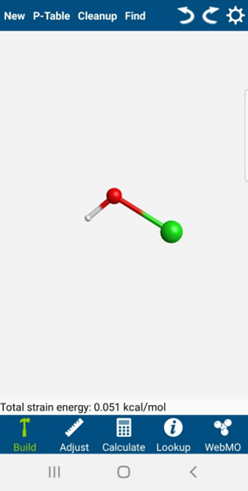
   • To select the element for the first atom, click on “P-Table” menu item. A periodic table will appear. Pick an element, like oxygen for example.

   • The periodic table will disappear and you will be back in the editor window. Click anywhere in the white area and a red sphere will appear. This red sphere represents an oxygen atom.

   • Now you are ready to add the hydrogen atom. Bring up the periodic table again and select hydrogen. To add a hydrogen atom that is bonded to the oxygen atom, click-drag (place the cursor on the oxygen, left-click and drag away from the oxygen atom while still holding the mouse button down). The hydrogen atom will be white. Repeat for the chlorine atom, which will be green.

   • If you need to add a double bond, simply click on one atom and then drag to the nearby atom where you want to add the double bond.

   • If you need to undo a step, the left pointing curved arrow at the top Chart, line chart Description automatically generated will undo your last action.

   • After building a molecule, perform an initial geometry optimization by choosing Clean-Up → Geometry before the next step.

 

2. After optimizing the geometry of your molecule, click on the “WebMO” icon on the bottom tool bar. 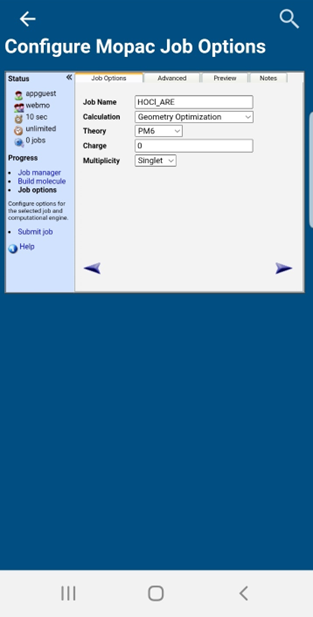Then click “Submit” on the top tool bar. Now you will be at the “Configure Mopac Job Options” page. Supply unique a job name that includes your initials that will help you identify the calculation. An example Job Name can be seen in the figure below. There should be no commas, symbols, parentheses, and/or spaces for the job name. Make sure the other settings match those in the example below (You will most likely have to change the Calculation to “Geometry Optimization”).
   
   Click the right pointing arrow in the bottom right of the screen to submit it.

3. Once the job is submitted, you will then be redirected back to the job manager page. The calculation should take less than one second, but it may take as much as 30 seconds for the queuing software to update the job status. Once the job status changes to a green “Complete” the calculation is finished. If the status is listed as a yellow “Running”, do not panic! The job is just waiting in line to make it to the computer cluster. If the status is listed as a red “Failed” then something went wrong. Look at the output as described in the next steps and ask your instructor if you cannot determine the issue.
   

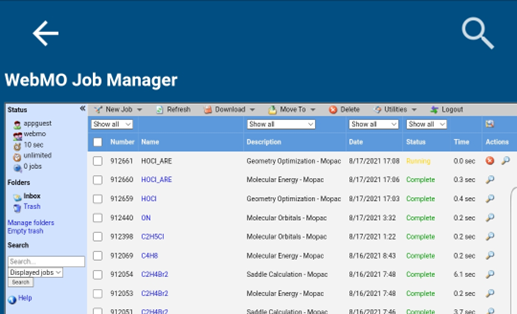
4. After the job completes, open the output by clicking the small magnifying glass icon to the right of your submitted job. A graphical representation of the molecule will be shown in the “Molecular Viewer” window. Now click on “Results” on the top tool bar. Record the Heat of Formation value, in kcal/mol, in Table A-1.
   

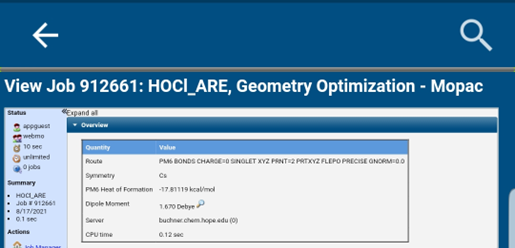
Part 2 – Predicting Polarity and Building 3D chemical compounds

In this part of the exercise, you will need to:

• Use VSEPR to draw the Lewis structures of the compounds listed in the table in the worksheet.
• Use WebMO to calculate the dipole moment for these compounds.

Computational Procedure:

1. Draw the Lewis structures for the compounds in the table. Before moving on to modeling them in WebMO, ask your instructor to check your Lewis Structures.
2. Using the procedure from Task 1, perform the quantum chemical calculations for the ground state geometry for the compounds listed in the table.
3. From your calculations, find the calculated dipole moment in Debye for each compound and record in the table.

Drawing Lewis Structures (a brief review):

1. Arrange atoms: when there is a central atom, it is usually the least electronegative. Hint: chemists usually list the central atom first in chemical formulas (e.g., \(\ce{CCl4}\) and \(\ce{CO3^2-}\) both have C as the central atom).
2. Determine total number of valence electrons in molecule or ion
3. Draw covalent bonds between atoms: Remember a covalent bond is two shared electrons
4. Beginning with terminal atoms, add enough electrons to each atom to give each atom an octet (or duet for hydrogen)
5. If any electrons are left over, place them on the central atom: Hint: some atoms may break the octet rule!
6. If the central atom has fewer electrons than an octet, form multiple (double or triple) bonds to the central atom to achieve an octet: Remember to keep track of the number of electrons you use!

 

This procedure was adapted from Simpson, Scott; Evanoski-Cole, Ashley; Gast, Kellie; Wedvik, Madeleine; Schneider, Patrick; and Klingensmith, Isaac. (2020). Quantum chemical exercise linking computational chemistry to general chemistry topics. Chemistry Teacher International. 3. 10.1515/cti-2019-0014.