1.3: The Physics Revolution of the Early 1900s (Relativity, Quantum)
- Page ID
- 203339
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
By about 1900, it seemed as though most fundamental physics problems had been solved. There were questions of chemistry, in that it not clear what matter was made of (whether there were atoms and whether atoms were made of anything else, but we had Newton's equations for particles, and Maxwell’s equations for light. Presumably these equations applied to whatever it is that matter is made of. It was very difficult to rationally account for Fraunhofer lines though, and, by 1911, there was a big problem with the “planetary” model of an atom of charged particles. But that was not all.
Two kinds of experiments in the late 1890s involving the light–matter interaction had yet to be clarified. These involved explaining the intensity of thermally emitted short-wavelength light (the ultraviolet catastrophe) and the energies of electrons ejected from metals by light (the photoelectric effect). The new theories that would be proposed to explain these effects would bend the mind and yet explain atomic spectra and the chemical bond.
1. Ultraviolet catastrophe
One thing scientists were struggling to understand was the distribution of frequencies emitted by heated objects. The ideal system to study was a heated metal box with a pin hole in it, as illustrated in the figure [#] below. The idea of having the box mostly closed is that the space inside the box is in thermal equilibrium with the box walls. So any electromagnetic fluctuations inside the box should have the same temperature as the box itself, and, therefore, the temperature of the light escaping through the hole is known. The reason to expect such thermal equilibrium is that the light itself must be generated by the chaotic motions of the charged particles that compose the box walls. (Thomson had recently shown that matter was made of charged particles).
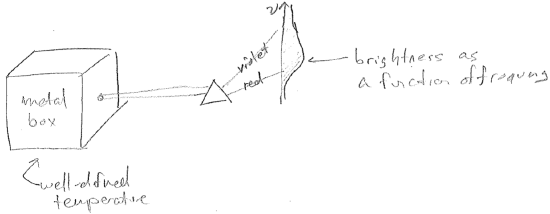
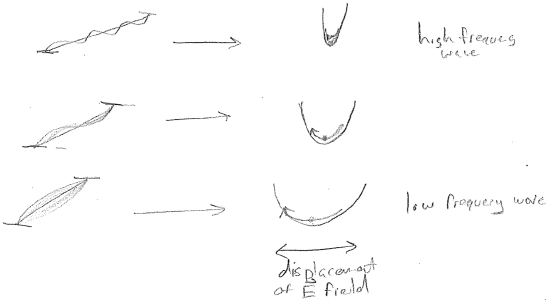
According to the statistical theory of Boltzmann, one only needs to know how much energy it costs to make a certain kind of electromagnetic fluctuation inside the box, in order to know the extent to which it will be present. Fluctuations requiring large energies will present to an expontially lesser extent, but still more likely if the temperature is increased. To analyze this, we associate each standing electromagnetic wave in the box with an oscillator as shown in the figure [#] above. Now, in order to compute the light intensity at each wavelength, we need to compute the average energy of each oscillator as a function of temperature. This is illustrated for a single wavelength in the figure [#] below.

Doing this analysis for each of the electromagnetic modes, Lord Rayleigh and James Jeans arrived at an energy density \(\rho\) as a function of wavelength, \(\lambda\), for a given temperature \(T\), which reads
\[
\rho(\lambda, T) = \frac{8 \pi k_\text{B} T}{\lambda^4}
\text{,}\]
where \(k_\text{B}\) is the Boltzmann constant. Here is a problem as big as Rutherford's unstable planetary atom. This energy density diverges for small \(\lambda\). Everything should glow intensely with high-frequency radiation all time, which it clearly does not!
The solution to this problem can be characterized as an act of mathematical desperation by Max Planck. He experimented with statistics, in which not every displacement of the electromagnetic field is allowed, but rather, only discrete values, as illustrated in the figures [#] below. Seen alternatively, each oscillator is only allowed a discrete set of energies. Clearly, if one plans on discretizing a continuous distribution, then a discretization scheme must be introduced; i.e., will it be discretized by the amplitude of the electric field \(|\vec{E}|\), or by the energy? Will all oscillators (electromagnetic frequencies) have the same discretization or will it depend on \(\lambda\)?

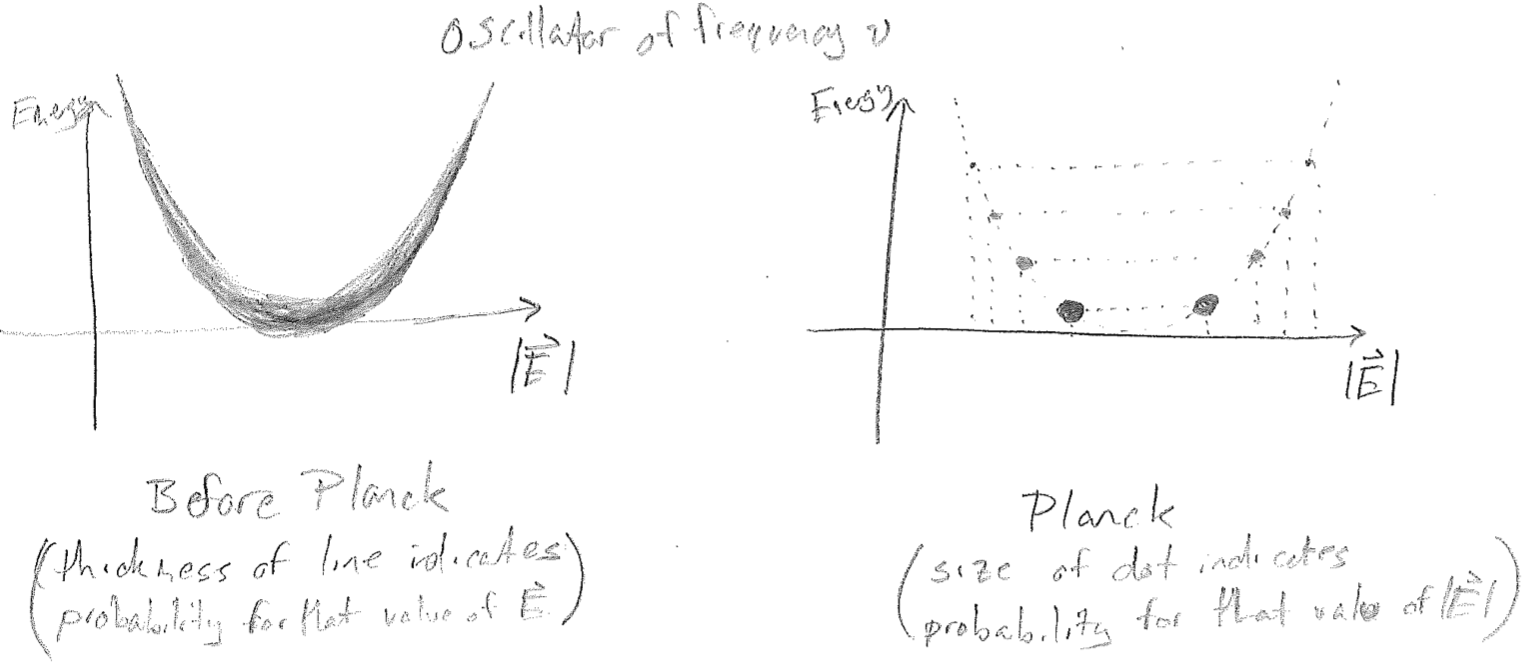
The scheme which Planck found to match experiment is when each oscillator is discretized as shown in the above figure [#], with evenly spaced energy jumps. Furthermore, the size of the energy jumps must depend on \(\lambda\), in order to damp the divergence of \(\rho\) at small \(\lambda\) (high \(\nu\)). The jumps must get larger for higher \(\nu\), and Planck found that this relationship is linear, as plotted in the figure [#] below, and so a parameter describing this (the slope of the line) needed to be introduced, and that parameter has dimensions of energy per frequency (\(\text{J}\cdot\text{s}\) in SI). This parameter, \(h = 6.62607004 \times 10^{-34} \text{J s}\), will later be understood to be a fundamental constant of nature and is called the Planck constant.

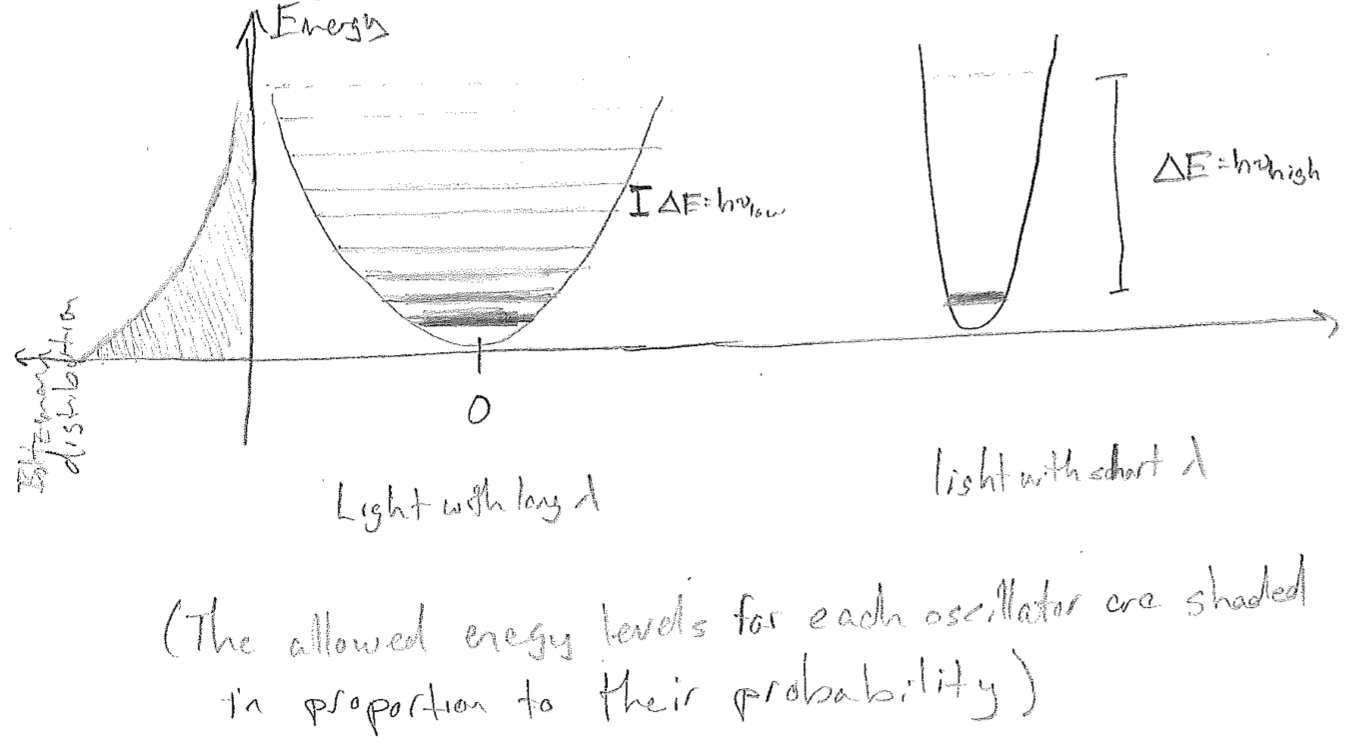
To see how this solves the problem, consider that the Boltzmann distribution (\(\text{e}^{-E / (k_\text{B} T)}\)) looks the same along the energy coordinate for all oscillators, as illustrated in the figure [#] below. For high frequency light, the linear increase in the size of the jumps is the argument to an exponentially decreasing probability function, so that the average energy of a high-frequency oscillator is, in a sense, penalized by not being able to fit many allowed levels into the energy regime of substantial probability. The end result of this is that it changes the net statistics that determine \(\rho\), yielding the Planck distribution, which matches experiments.
\[
\rho(\lambda,T) = \frac{8 \pi h c}{\lambda^5 (\text{e}^{hc / (\lambda k_\text{B} T)}-1)}
\]
Foremostly, as \(\lambda \rightarrow 0\), the exponential diverges faster than \(\lambda^5\), damping the divergence that would otherwise be there. For large \(\lambda\), we recover the Rayleigh–Jeans distribution by expanding the exponential,
\[
\text{e}^{hc / (\lambda k_\text{B} T)} = \frac{hc}{\lambda k_\text{B} T} + \frac{1}{2}\left(\frac{h c}{\lambda k_\text{B} T}\right)^2 + \cdots
\text{,}\]
giving
\[
\lim _{\lambda \rightarrow \infty} \rho(\lambda, T) =
\frac{8 \pi h c}{\lambda^5 \left(\frac{hc}{\lambda k_\text{B} T}\right)}
=\frac{8 \pi k_\text{B} T}{\lambda^4}
\text{.}\]
This illustrates something we will see repeatedly but will not dwell on here. There always exists some limit in which the quantum result yields the classical result. It must be like this or else our classical-appearing reality could not emerge from on inherently quantum universe.
2. Photoelectric effect
Recall from our history of the atom that, in 1897, Thomson had demonstrated that matter could be decomposed into charged particles whose motions were responsible for electrical currents. It was also being observed that, under certain circumstances, light could liberate charged particles from a metal surface. By an analysis of their properties (e.g., mass-to-charge ratio), these were most likely the same electrons Thomson had discovered. In an abstraction of the experimental setup, the effect looks as found in the figure [#] below.

The light being shone an the metal is characterized by two parameters, its frequency \(\nu\) and its intensity \(I\) (colloquially, its brightness). Recalling that all waves, including light, carry energy. Brighter light must be characterized by more energy per time focused on a specific area; the SI units for intensity are \(\frac{\text{J}}{\text{m}^2 \text{s}}\). That said, it stands for reason that brighter light should deposit more energy into each outgoing electron over the time taken to eject it. So, the expected experimental result is as illustrated in the plot in the figure [#] below.

Instead of the expected result, the plots shown in the figure [#] below were observed. Taken together, these two results at least conserve energy because the increased energy from increased intensity is expended to eject more electrons, but it was rather perplexing as to why each electron should have the same energy, and regardless of intensity. The clue to the underlying “new physics” (results which lead to new or modified theories) is that the kinetic energy can be varied by changing the frequency, but only above a set threshold \(\nu_0\), as seen in the plot in the figure [#] below.
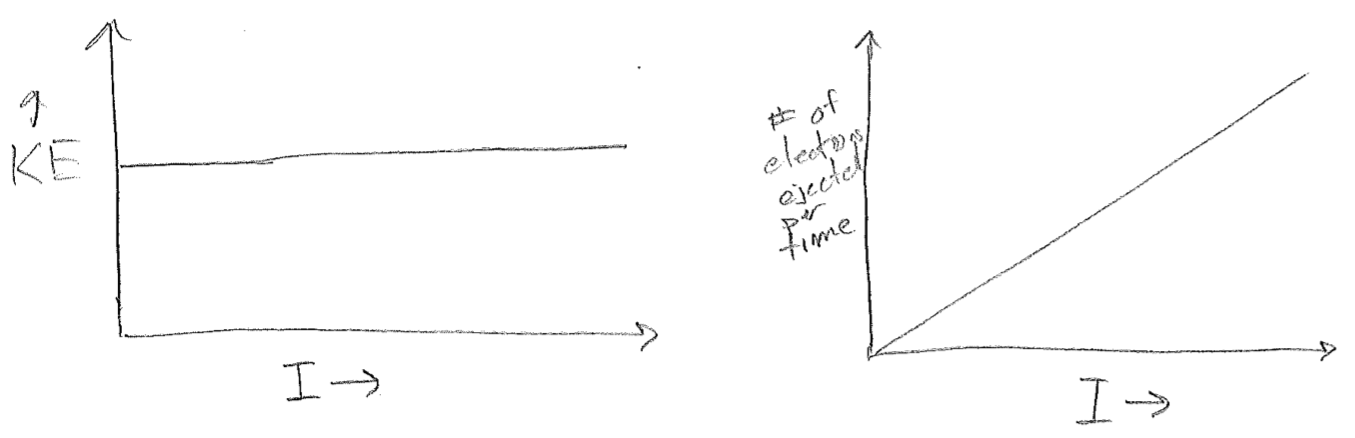
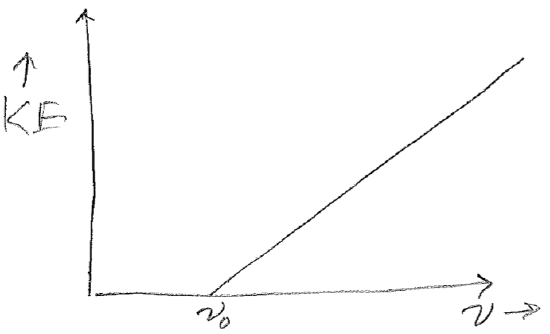
Before we proceed to the interpretation, here is the most shocking part. Although \(\nu_0\) depends on the identify of the metal, the slope of the line in this figure is \(h\), Planck’s constant! There is not any trivially obvious reason why Planck’s constant should appear again (i.e., the experiments have no overlapping components and are not redundant).
An interesting aspect of all of this is that humankind’s first encounter with controlled electricity (before understanding electrons to be involved) was through electrochemical cells. That is important because we already had some knowledge of how the chemical identity of materials interacted with electricity. There was already a notion of a work function \(\Phi^\text{(chem)}\), which describes the energetic “penalty” for oxidizing a certain metal in the anode in an electrochemical cell. Today we understand oxidation in terms of atoms losing electrons, but that was not yet clear at that time. It was noted then though that, in the photoelectric effect, metals with a high \(\Phi^\text{(chem)}\) required a higher \(\nu_0\) to begin ejecting electrons.
Since \(h(\nu-\nu_0)\) could be correlated to the kinetic energy of the escaping electron, then it was reasonable to associate \(h\nu\) with the total energy imported by the light and \(h\nu_0\) with the energy needed to simply free an electron, leaving the difference to be deposited into the kinetic energy of the electron. This interpretation made good sense in light of the fact that there was a correlation between those metals with a large values of \(h \nu_0\) and \(\Phi^\text{(chem)}\), where the nature of chemical oxidation in terms of electrons was simultaneously becoming understood. For this reason \(h \nu_0\) itself began to be called the work function, \(\Phi\). When all put together, the formula for the kinetic energy of a photoelectron is
\[
E_\text{kinetic} = h\nu - \Phi
\text{.}\]
It should be noted that \(\Phi\) and \(\Phi^\text{(chem)}\) do not have the same value for any given metal though. One (\(\Phi\)) occurs under high vacuum and the other \(\Phi^\text{(chem)}\) in an aqueous solution of mobile counter-balancing ions.
The story is being told in a sort of “leading” way and it has by-the-way been made clear that the interpretation of \(h\nu\) must be that this is the amount of energy each electron absorbs from the light. However, the story as it unfolded was a mess. Though we do not go into the details of all of the false starts the person who put it all together, in 1905, was Albert Einstein.
In addition to clarifying that the experimental results of the photoelectric effect could be explained by the interpretation that each electron absorbs exactly \(h\nu\) of energy from the electromagnetic field, he also connected this to the results of Planck. Planck's results suggested that energy is imparted to the electromagnetic field itself in discrete amounts of \(\pm h\nu\). This unit of energy might be viewed as some sort of fundamental indivisible packet of energy, perhaps a particle? The photoelectric effect could then be conceptualized as light consisting of a stream of these light “particles,” each with energy \(h\nu\). Each electron may absorb one, and only one packet, using part of the energy to liberate itself from the metal, and the balance to accelerate to the complementary kinetic energy. This explained the threshold behavior and the slope of \(h\). More intense light consists of more “particles” allowing for the ejection of more electrons, also in accord with experiment.
You might have noticed the suspicious absence of the word photon in the above. Einstein did not use that word. Perhaps, it would be better if no one ever had. Envisioning light as consisting of classical-like particles is a poor conceptualization. The point of view adopted in this text (openly, a subjective interpretation) is that there are no particles of anything at all, in the sense they are understood in classical mechanics. Everything is a wave. There are two broad classes of quantum waves: those that mediate forces (electromagnetic, gravitational, etc.), and those that build matter (electrons, nuclei, etc.). The distinction between them is one of a rather abstract symmetry, but we would be getting way ahead of ourselves to discuss that now. The point is that everything is a wave, and yet wave amplitudes can be discretized, such that measuring how much wave is present can be mapped onto counting integers, like particles.
“Photon” was originally pejorative term for the “stupid” idea that light could be counted like particles. It was coined by the famous chemist Gilbert Newton Lewis and consisted of appending to the Greek root for light, “phot,” the suffix “on,” to signify its particle nature (along with electrons, protons, etc.). It is sort of a shame that Lewis would spend much trouble fighting the notion that anything quantum is meaningful because his beloved bonds and valency would eventually require it for explanation. Although we will take great pains in this text to disabuse students of the notion that light is a stream of hard little photon particles, irrespective of interpretation, a name is needed for the quantized units of electromagnetic waves, and so, photon it is.
Einstein would eventually win the Nobel prize for his clarification of the photoelectric effect. Many are surprised that he did not win it for the theory of relativity, but the reader should realize that the problems of the UV catastrophe and photoelectric effect were pressing and troublesome. The world of physics seemed to be busting at the seams; nothing about the structure of matter at the microscopic scale made any sense, and \(E=h\nu\) was at least a solid anchor in this tumult. By comparison, the theory of relativity solved some rather esoteric problems. On top of that, relativity was weird in the sense there is no universal “now,” and it was hard to verify that Einstein's theory was any more valid than the next weird idea.
It is worth noting that 1905 was an amazing year for physics, and for Einstein especially. In addition to clarifying the photoelectric effect, he contributed to the final acceptance of the existance of atoms via calculations concerning Brownian motion (see previous section). Furthermore, in this same year, now known as his annus mirabilis (year of miracles), he published the special theory of relativity. We will now show how one result from relativity, applied to a third experiment, sends the world of physics tumbling head-log into quantum mechanics.
3. Compton scattering
To truly appreciate the significance of the scattering experiments done by Arthur Holly Compton, it is necessary to understand at least the coarsest features of Einstein’s special theory of relativity. We begin with the puzzle that the speed of light had been observed to be independent of the velocity of the observer. It is logically impossible to reconcile this fact with “normal” Newtonian/Euclidean space and time; in such a picture, velocity vectors must add and subtract. The only resolution to this is that space and time are somehow not distinct from each other. When an observer changes velocity, the space and time axes change direction in space-time from the observer's perspective, such that the speed of any given light ray appears the same before and after. As a further consequence of mixing space and time, energy must not be distinct from momentum. Note that the fundamental constant underlying relativity, the speed of light \(c\), can be viewed as a conversion factor between space and time, having dimensions of \(\frac{\text{m}}{\text{s}}\) (in SI units), which is the same as for a conversion factor between energy and momentum \(\frac{\text{kg}\,(\text{m}/\text{s})^2}{\text{kg m}/\text{s}}\).
Informally, we may say that there is a momentum associated with an the propagation of an object through time, equal to \(mc\), where \(m\) is the rest mass of the body in question. Einstein showed that, in order to self consistently account for all observations, the relativistic formula for the energy of a particle must be
\[
E = c \sqrt{(m c)^2 + p^2}
\text{,}\]
where \(mc\) and \(p\) are the time-like and space-like momenta respectively. A quick exercise in power series expansion shows that, for small \(p\)
\[
E = m c^2 + \frac{p^2}{2 m} + \cdots
\text{.}\]
For a particle with mass, we immediately recognize \(p^2/(2m) = (1/2)mv^2\) as the classical kinetic energy. As long as we are never concerned with objects near the speed of light (i.e., small \(p\)), the classical formula is sufficient, and relativity just adds an inconsequential constant shift to the energy, interpreted as some energy needed to create the particle.
The interesting aspect of Einstein's equation with reference quantum mechanics is the energy of a massless particle. In the theory of relativity, no massive object may move at the speed of light, so photons, if thought of as particles, must not be allowed to have mass, but we have seen that they are energy. So we arrive at
\[
E = c \sqrt{p^2} = c p
\text{,}\]
and, therefore, the conclusion is that photons, if they exist, must carry momentum \(E/c\). In 1923 such a momentum was measured by Compton, in experiments where light deflected the trajectory of electrons and scattered the light, as illustrated schematically in the figure [#] below.

The change in momentum of the electron shows unambiguously that light carries momentum. Using conservation of momentum, Compton was able to solve for the momentum of photons, treating them as classical particles. The momentum was found to depend on the wavelength of the light as
\[
p_\text{photon} = \frac{h}{\lambda_\text{light}}
\text{.}\]
This is now the third seemingly unrelated occurrence of Planck's constant. It is becoming more clear that \(h\) is a fundamental constant of nature. Furthermore, inserting this momentum into Einstein's equation for the energy of a particle we arrive at (using \(c=\lambda\nu\))
\[
E = c p = c \frac{h}{\lambda} = c \frac{h}{c / \nu} = h \nu
\text{,}\]
which is consistent with the energy of a photon, already posited from the photoelectric effect.
Light now appears to consist of photons which are particles in every sense of the word, at least to the extent that anything is a particle. But there is a already so much evidence that light behaves as waves. Maxwell's equations are wave equations and even Planck's derivations, interpreted in terms of photons, rest on that. Light reflects, refracts, and diffracts. Either we need to seriously revise our notion of what a wave is, by representing it as a stream of discrete bodies, or we need to reckon with the idea that we may not really understand what a particle is. Interpretation is always uncertain and malleable, but the latter appears a more efficient explanation of what is to come.
4. Bohr, the atom, and De Broglie
At this point, we have come to the conclusion that light can be interpreted in terms of particle-like quanta called photons. We ended this part of the story with Compton’s experiment in 1923. The quantum revolution will be substantially complete by 1925, when a theory of matter traveling as waves is forwarded. To follow this line of history, let us back up a bit in time to 1913. The photoelectric effect had been clarified eight years earlier by Einstein, and, two years prior to that, Rutherford discovered that the electrons in matter are best pictured as swarming around heavy, positive nuclei. This planetary model was problematic because electrons should lose energy and crash into the nuclei, if both Newton’s and Maxwell’s equations are to be satisfied.
Niels Bohr postulated in 1913 that perhaps only certain orbits around the atom are stable, but for reasons that were unclear, at best. One of the advantages of this idea is that it served to explain atomic spectra, the fact that atoms were known since the 1800s to absorb and emit only certain wavelengths of light. If Einstein were right about the relationship between photon energy and the frequency of light, then having atoms with only specific allowed energy levels (reminiscent of those proposed by Planck for light itself) would explain why only certain frequencies could be absorbed or emitted. Starting with the experimentally known frequencies for the hydrogen atom (converted energy gaps between the levels), Bohr solved for the angular momentum of the stable planetary orbits that would provide this experimental spectrum. Amazingly, he found that the angular momenta of these orbits are separated by \(h/(2\pi)\), a unit of angular momentum that will commonly be abbreviated as \(\hbar\). Planck's constant has made yet another appearance. This appearance of \(h\) is a hint of an universal physics underlying both photons and electrons.
In order for the eventual explanation of these orbits to be united with classical mechanics, it would be hoped that, as the election orbits start to take on macroscopic dimensions at high energy, the familiar classical limit would be applicable. It is, and this enduring principle is known as the quantum–classical correspondence principle. In detail, when one converts the energy gaps between high-lying orbits to frequency, one obtains exactly the frequency of the classical orbital motion of an electron with that energy, as it moves around the nucleus.
The Bohr model of the atom, and extensions by Arnold Sommerfeld, had some major successes and failures. Among the successes was its consistency with later experiments by Otto Stern and Walther Gerlach, which showed that angular momentum is allowed to only have certain discrete (quantized) values for atoms. To understand the experiment, consider that a charged particle with angular momentum can be interpreted as setting up an electrical current (charge moving in a circle) and, therefore, a magnetic field. This can interact with an external magnet while it moves and change the direction of travel of an atom. When done with a beam of silver atoms emanating from an oven, as shown in the figure [#] below, one beams splits into two, indicating that the angular momentum indeed takes on one of two discrete values. The experiment is sort of confusing at the detailed level (i.e., why does the beam split only in two with so many electrons?), but the fact remains that angular momentum is quantized. This experiment will be discussed more later in this text; in fact, the Stern–Gerlach experiment will be understood in terms of electron spin.


Among the failures of the Bohr model is that no generalization of it worked for atoms with more than one electron, nor provided any insight into the chemical bond. Furthermore, there were vagaries in its theoretical footing. Is the electron indeed circling the electron? If so, why are only these orbits stable, with the lowest orbit perpetually stable against radiating away energy?
Now flash forward again to 1924, one year after Compton verifies that photons have every bit the same particle character as any other particle. Compton has provided us with
\[
p_\text{photon} = \frac{h}{\lambda_\text{light}}
\]
A young theorist by the name of Louis De Broglie then asserted that perhaps particles themselves are some kind of wave, and he proposed that, for these matter waves, the following should hold
\[
p_\text{particle} = \frac{h}{\lambda_\text{matter}}
\]
Due to the enduring success of this hypothesis, the wavelength of a material particle (a matter wave) is still called its De Broglie wavelength. The universality of a relationship between momentum and wavelength is especially appealing in light of relativity. Recalling that momentum is the spatial analog of energy and that \(\bar{\nu}=1/\lambda\) is the “spatial frequency” (waves per meter), then the De Broglie relationship, \(p=h\bar{\nu}\), is the analog of \(E=h\nu\). Since the calculations of Bohr suggested that energy and frequency are related for matter as well as for light, then relativity suggests that for matter, momentum is related to wavelength, which is born out in the De Broglie relationship.
In an immediate success of the matter-wave hypothesis, De Broglie showed that the quantized orbits of Bohr were exactly those for which the momentum–wavelength relationship led to an electron completing an integer number of wave cycles as it “circled” the atom. This gave meaning to the otherwise absurd hypothesis of Bohr that these orbits were somehow special. These orbits could be interpreted as standing waves, waves whose form do not change in time, and therefore lead to no radiation, since they are, in a sense, not moving. This is also a first hint at the relationship between quantization and mathematical restrictions placed on the forms of waves, called boundary conditions.
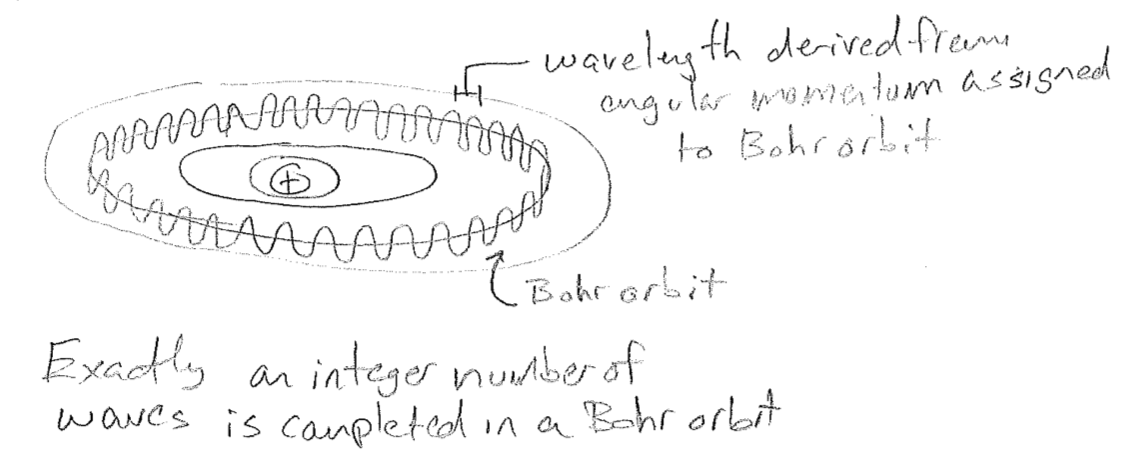
5. Confirmation of matter waves, the birth of quantum mechanics
There were still some problems as of 1924. To start with, it is unclear why or if a particle acts as a wave only along the direction it is traveling. However, the matter-wave idea is now firmly entrenched, and it seems unlikely to be shown to be wrong. In 1927, experiments by Clinton Davisson and Lester Germer directly showed wave-like properties for electrons. Electrons were reflected off of the surface of a Ni crystal lattice. Since the lattice spacing had dimension similar to the electron wavelength, an interference pattern, indicative of wave behavior was observed, as illustrated in the figure [#] below.
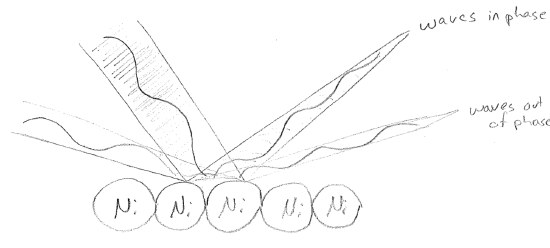
In 1925, ahead of the diffraction experiments, a more complete theory of quantum mechanics was developed in two different forms, independently and almost simultaneously, by Werner Heisenberg (matrix mechanics) and Erwin Schrödinger (wave mechanics). At the same time, Max Born gave interpretation to the particle wavefunction in terms of the probability that the particle would be found at any given location via a classical measurement. Although the precise meaning of what constitutes a "classical measurement" are still disputed at a philosophical level, the formalism has shown itself to be unambiguously useful at a practical level. This work, comprising the wave equations for matter and their connection to measurement, is the subject of the rest of this text.
6. Summary of further and future consequences
In 1926 Wolfgang Pauli used the formalism of Heisenberg to derive the spectrum of the hydrogen atom, this time with clarity about the origin of the energetic quantization. He would assert the property of electron spin, which will be necessary to understand the rest of the atoms, as discussed later in this text. At almost the same time Paul Dirac was developing a fully relativistic quantum theory, and, in this theory, electron spin is a result, rather than an assertion. Dirac's framework also predicts antimatter (observed by Carl Anderson in 1932) by lending a wave interpretation to Einstein's equivalence of matter and energy. In this interpretation \(mc^2\) is the energy needed to produce a wave that characterizes a particle of mass \(m\). By 1939, quantum mechanics had even clarified the principles underlying a covalent bond, famously recorded in book by Linus Pauling.
Of great relevance to chemistry, and the basis of a substantial fraction of this text, is that application of the principles of quantum mechanics to the motions of molecules forms the basis of the field of spectroscopy, which is our primary source of information about the tiny quantum world. The basic process of spectroscopy is illustrated schematically in the figure [#] below, in which the change in energy \(\Delta E\) of some material system is matched to the energy \(h\nu\) of a photon that causes a transition. Doing detailed calculations for different cases of this situation will be of great practical value throughout our study of quantum mechanics.

Presently, however, we will focus the abstract theoretical significance of spectroscopy. Together, the equations (which are the same equation under relativity)
\[\begin{align}
E &= h\nu \\
p &= h \bar{\nu} = \frac{h}{\lambda}
\end{align}
\]
suggest new meaning to the very notions of energy and momentum. Because they both work for both matter and light, it seems that energy is fundamentally and universally equivalent to frequency, and that momentum is universally equivalent to (inverse) wavelength. Recall that \(h\) can be thought of as a conversion factor between energy and frequency or momentum and inverse wavelength. In a picture where the entire universe (matter and energy) consists of waves, energy and momentum conservation are then consequences of resonance conditions being satisfied. That is, two waves do not interact unless they have matching frequencies (in space, time, or space-time). This has already been hinted at by the work of Niels Bohr. Recall that his model was based on energy conservation (photon energy = atomic transition energy); he discovered that, for the outer levels of his model of the atom, the orbitals that satisfied the energy requirement also had the same classical orbital frequency as the light whose photons bear that energy, as illustrated in the figure below [#]. This is suggestive that frequencies of matter oscillations also account for their energetics. Although, Bohr's correspondence principle did not hold for the lower orbits, as the full theory of quantum mechanics is developed, we will see how energy is indeed equivalent to frequency.



