5.6: Hess's Law

Learning Objectives

• To use Hess’s law and thermochemical cycles to calculate enthalpy changes of chemical reactions.

Because enthalpy is a state function, the enthalpy change for a reaction depends on only two things: (1) the masses of the reacting substances and (2) the physical states of the reactants and products. It does not depend on the path by which reactants are converted to products. If you climbed a mountain, for example, the altitude change would not depend on whether you climbed the entire way without stopping or you stopped many times to take a break. If you stopped often, the overall change in altitude would be the sum of the changes in altitude for each short stretch climbed. Similarly, when we add two or more balanced chemical equations to obtain a net chemical equation, ΔH for the net reaction is the sum of the ΔH values for the individual reactions. This principle is called Hess’s law, after the Swiss-born Russian chemist Germain Hess (1802–1850), a pioneer in the study of thermochemistry. Hess’s law allows us to calculate ΔH values for reactions that are difficult to carry out directly by adding together the known ΔH values for individual steps that give the overall reaction, even though the overall reaction may not actually occur via those steps.

Hess Law argues that ΔH for the net reaction is the sum of the ΔH values for the individual reactions. This is nothing more than arguing ΔH is a state function.

We can illustrate Hess’s law using the thermite reaction. The overall reaction shown in Equation \(\ref{5.6.1}\) can be viewed as occurring in three distinct steps with known ΔH values. As shown in Figure 5.6.1, the first reaction produces 1 mol of solid aluminum oxide (Al₂O₃) and 2 mol of liquid iron at its melting point of 1758°C (part (a) in Equation \(\ref{5.6.1}\)); the enthalpy change for this reaction is −732.5 kJ/mol of Fe₂O₃. The second reaction is the conversion of 2 mol of liquid iron at 1758°C to 2 mol of solid iron at 1758°C (part (b) in Equation 5.6.1); the enthalpy change for this reaction is −13.8 kJ/mol of Fe (−27.6 kJ per 2 mol Fe). In the third reaction, 2 mol of solid iron at 1758°C is converted to 2 mol of solid iron at 25°C (part (c) in Equation \(\ref{5.6.1}\)); the enthalpy change for this reaction is −45.5 kJ/mol of Fe (−91.0 kJ per 2 mol Fe). As you can see in Figure 5.6.1, the overall reaction is given by the longest arrow (shown on the left), which is the sum of the three shorter arrows (shown on the right). Adding parts (a), (b), and (c) in Equation 5.6.1 gives the overall reaction, shown in part (d):

\[ \small \begin{matrix}
2Al\left ( s, \; 25 ^{o}C \right ) + 2Fe_{2}O_{3}\left ( s, \; 25 ^{o}C \right )& \rightarrow & 2Fe\left ( l, \; 1758 ^{o}C \right ) + 2Al\left ( s, \; 1758 ^{o}C \right ) & \Delta H=-732.5 \; kJ& \left ( a \right ) \\
2Fe\left ( l, \; 1758 ^{o}C \right ) & \rightarrow & 2Fe\left ( s, \; 1758 ^{o}C \right ) & \Delta H=-\;\; 27.6 \; kJ & \left ( b \right )\\
2Fe\left ( s, \; 1758 ^{o}C \right ) + 2Al\left ( s, \; 1758 ^{o}C \right ) & \rightarrow & 2Fe\left ( l, \; 25 ^{o}C \right ) + 2Al\left ( s, \; 25 ^{o}C \right ) & \Delta H=-\;\; 91.0 \; kJ & \left ( c \right )\\
2Al\left ( s, \; 25 ^{o}C \right ) + 2Fe_{2}O_{3}\left ( s, \; 25 ^{o}C \right ) & \rightarrow & 2Al\left ( s, \; 25 ^{o}C \right ) + 2Fe_{2}O_{3}\left ( s, \; 25 ^{o}C \right ) & \Delta H=-852.2 \; kJ & \left ( d \right )
\end{matrix} \label{5.6.1} \]

The net reaction in part (d) in Equation \(\ref{5.6.1}\) is identical to Equation \(\ref{5.4.9}\). By Hess’s law, the enthalpy change for part (d) is the sum of the enthalpy changes for parts (a), (b), and (c). In essence, Hess’s law enables us to calculate the enthalpy change for the sum of a series of reactions without having to draw a diagram like that in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): Energy Changes Accompanying the Thermite Reaction. Because enthalpy is a state function, the overall enthalpy change for the reaction of 2 mol of Al(s) with 1 mol of Fe₂O₃(s) is −851.1 kJ, whether the reaction occurs in a single step (ΔH₄, shown on the left) or in three hypothetical steps (shown on the right) that involve the successive formation of solid Al₂O₃ and liquid iron (ΔH₁), solid iron at 1758°C (ΔH₂), and solid iron at 25°C (ΔH₃). Thus ΔH₄ = ΔH₁ + ΔH₂ + ΔH₃, as stated by Hess’s law.

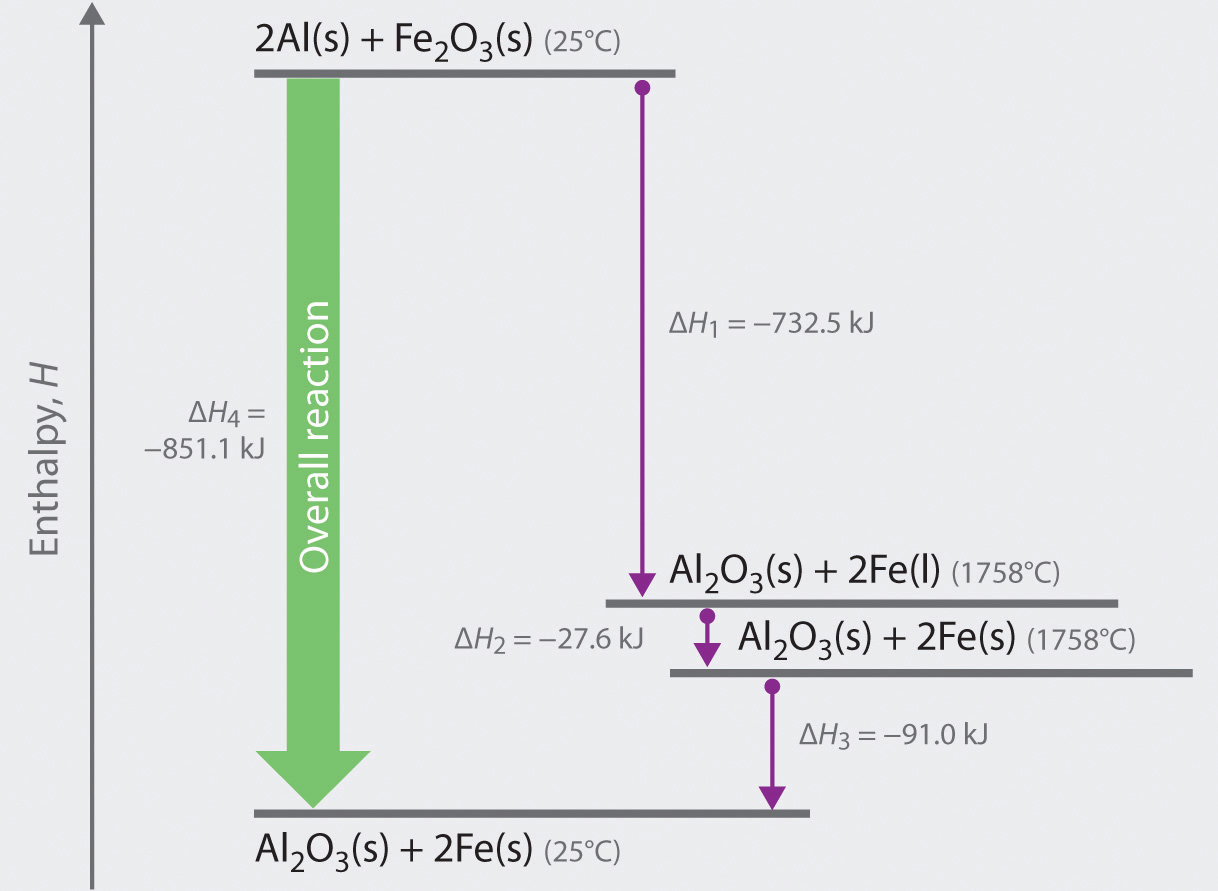
Comparing parts (a) and (d) in Equation \(\ref{5.6.1}\) also illustrates an important point: The magnitude of ΔH for a reaction depends on the physical states of the reactants and the products (gas, liquid, solid, or solution). When the product is liquid iron at its melting point (part (a) in Equation \(\ref{5.6.1}\)), only 732.5 kJ of heat are released to the surroundings compared with 852 kJ when the product is solid iron at 25°C (part (d) in Equation \(\ref{5.6.1}\)). The difference, 120 kJ, is the amount of energy that is released when 2 mol of liquid iron solidifies and cools to 25°C. It is important to specify the physical state of all reactants and products when writing a thermochemical equation.

When using Hess’s law to calculate the value of ΔH for a reaction, follow this procedure:

1. Identify the equation whose ΔH value is unknown and write individual reactions with known ΔH values that, when added together, will give the desired equation. We illustrate how to use this procedure in Example \(\PageIndex{1}\).
2. Arrange the chemical equations so that the reaction of interest is the sum of the individual reactions.
3. If a reaction must be reversed, change the sign of ΔH for that reaction. Additionally, if a reaction must be multiplied by a factor to obtain the correct number of moles of a substance, multiply its ΔH value by that same factor.
4. Add together the individual reactions and their corresponding ΔH values to obtain the reaction of interest and the unknown ΔH.

Example \(\PageIndex{1}\)

When carbon is burned with limited amounts of oxygen gas (O₂), carbon monoxide (CO) is the main product:

\[ \left ( 1 \right ) \;2C\left ( s \right ) + O_{2}\left ( g \right ) \rightarrow 2CO\left ( g \right ) \; \;\ \; \Delta H=-221.0 \; kJ \]

When carbon is burned in excess O₂, carbon dioxide (CO₂) is produced:

\[ \left ( 2 \right ) \;C\left ( s \right ) + O_{2}\left ( g \right ) \rightarrow CO_{2}\left ( g \right ) \; \;\ \; \Delta H=-393.5 \; kJ \]

Use this information to calculate the enthalpy change per mole of CO for the reaction of CO with O₂ to give CO₂.

Given: two balanced chemical equations and their ΔH values

Asked for: enthalpy change for a third reaction

Strategy:

1. After balancing the chemical equation for the overall reaction, write two equations whose ΔH values are known and that, when added together, give the equation for the overall reaction. (Reverse the direction of one or more of the equations as necessary, making sure to also reverse the sign of ΔH.)
2. Multiply the equations by appropriate factors to ensure that they give the desired overall chemical equation when added together. To obtain the enthalpy change per mole of CO, write the resulting equations as a sum, along with the enthalpy change for each.

Solution:

A We begin by writing the balanced chemical equation for the reaction of interest:

\[ \left ( 3 \right ) \;CO\left ( g \right ) + \frac{1}{2}O_{2}\left ( g \right ) \rightarrow CO_{2}\left ( g \right ) \; \;\ \; \Delta H_{rxn}=? \]

There are at least two ways to solve this problem using Hess’s law and the data provided. The simplest is to write two equations that can be added together to give the desired equation and for which the enthalpy changes are known. Observing that CO, a reactant in Equation 3, is a product in Equation 1, we can reverse Equation (1) to give

\[ 2CO\left ( g \right ) \rightarrow 2C\left ( s \right ) + O_{2}\left ( g \right ) \; \;\ \; \Delta H=+221.0 \; kJ \]

Because we have reversed the direction of the reaction, the sign of ΔH is changed. We can use Equation 2 as written because its product, CO₂, is the product we want in Equation 3:

\[ C\left ( s \right ) + O_{2}\left ( g \right ) \rightarrow CO_{2}\left ( s \right ) \; \;\ \; \Delta H=-393.5 \; kJ \]

B Adding these two equations together does not give the desired reaction, however, because the numbers of C(s) on the left and right sides do not cancel. According to our strategy, we can multiply the second equation by 2 to obtain 2 mol of C(s) as the reactant:

\[ 2C\left ( s \right ) + 2O_{2}\left ( g \right ) \rightarrow 2CO_{2}\left ( s \right ) \; \;\ \; \Delta H=-787.0 \; kJ \]

Writing the resulting equations as a sum, along with the enthalpy change for each, gives

\[ \begin{matrix}
2CO\left ( g \right ) & \rightarrow & \cancel{2C\left ( s \right )}+\cancel{O_{2}\left ( g \right )} & \Delta H & = & -\Delta H_{1} & = & +221.0 \; kJ \\
\cancel{2C\left ( s \right )}+\cancel{2}O_{2}\left ( g \right ) & \rightarrow & 2CO_{2} \left ( g \right ) & \Delta H & = & -\Delta 2H_{2} & = & -787.0 \; kJ \\
2CO\left ( g \right ) + O_{2}\left ( g \right ) & \rightarrow & 2CO_{2} \left ( g \right ) & \Delta H & = & & -566.0 \; kJ
\end{matrix} \]

Note that the overall chemical equation and the enthalpy change for the reaction are both for the reaction of 2 mol of CO with O₂, and the problem asks for the amount per mole of CO. Consequently, we must divide both sides of the final equation and the magnitude of ΔH by 2:

\[ \begin{matrix}
CO\left ( g \right ) + \frac{1}{2}O_{2}\left ( g \right ) & \rightarrow & CO_{2} \left ( g \right ) & \Delta H & = & & -283.0 \; kJ
\end{matrix} \]

An alternative and equally valid way to solve this problem is to write the two given equations as occurring in steps. Note that we have multiplied the equations by the appropriate factors to allow us to cancel terms:

\( \small \begin{matrix}
\left ( A \right ) & 2C\left ( s \right ) + O_{2}\left ( g \right ) & \rightarrow & \cancel{2CO\left ( g \right )} & \Delta H_{A} & = & \Delta H_{1} & = & +221.0 \; kJ \\
\left ( B \right ) &\cancel{2CO\left ( g \right )} + O_{2}\left ( g \right ) & \rightarrow & 2CO_{2} \left ( g \right ) & \Delta H_{B} & & & = & ? \\
\left ( C \right ) & 2C\left ( s \right ) + 2O_{2}\left ( g \right ) & \rightarrow & 2CO_{2} \left ( g \right ) & \Delta H & = 2\Delta H_{2} & =2\times \left ( -393.5 \; kJ \right ) & =-787.0 \; kJ
\end{matrix} \)

The sum of reactions A and B is reaction C, which corresponds to the combustion of 2 mol of carbon to give CO₂. From Hess’s law, ΔH_A + ΔH_B = ΔH_C, and we are given ΔH for reactions A and C. Substituting the appropriate values gives

\[ \begin{matrix}
-221.0 \; kJ + \Delta H_{B} = -787.0 \; kJ \\
\Delta H_{B} = -566.0
\end{matrix} \]

This is again the enthalpy change for the conversion of 2 mol of CO to CO₂. The enthalpy change for the conversion of 1 mol of CO to CO₂ is therefore −566.0 ÷ 2 = −283.0 kJ/mol of CO, which is the same result we obtained earlier. As you can see, there may be more than one correct way to solve a problem.

Exercise \(\PageIndex{1}\)

The reaction of acetylene (C₂H₂) with hydrogen (H₂) can produce either ethylene (C₂H₄) or ethane (C₂H₆):

\[ \begin{matrix}
C_{2}H_{2}\left ( g \right ) + H_{2}\left ( g \right ) \rightarrow C_{2}H_{4}\left ( g \right ) & \Delta H = -175.7 \; kJ/mol \; C_{2}H_{2} \\
C_{2}H_{2}\left ( g \right ) + 2H_{2}\left ( g \right ) \rightarrow C_{2}H_{6}\left ( g \right ) & \Delta H = -312.0 \; kJ/mol \; C_{2}H_{2}
\end{matrix} \]

What is ΔH for the reaction of C₂H₄ with H₂ to form C₂H₆?

Answer: −136.3 kJ/mol of C₂H₄

Summary

Hess's law is arguing the overall enthalpy change for a series of reactions is the sum of the enthalpy changes for the individual reactions. For a chemical reaction, the enthalpy of reaction (ΔH_rxn) is the difference in enthalpy between products and reactants; the units of ΔH_rxn are kilojoules per mole. Reversing a chemical reaction reverses the sign of ΔH_rxn. The magnitude of ΔH_rxn also depends on the physical state of the reactants and the products because processes such as melting solids or vaporizing liquids are also accompanied by enthalpy changes: the enthalpy of fusion (ΔH_fus) and the enthalpy of vaporization (ΔH_vap), respectively. The overall enthalpy change for a series of reactions is the sum of the enthalpy changes for the individual reactions, which is Hess’s law. The enthalpy of combustion (ΔH_comb) is the enthalpy change that occurs when a substance is burned in excess oxygen.

Contributors and Attributions

• Modified by Joshua Halpern (Howard University)