2.1: The Atomic Theory of Matter
- Page ID
- 91133
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Explain how all matter is composed of atoms.
- Describe the modern atomic theory.
Take some aluminum foil. Cut it in half. Now there are two smaller pieces of aluminum foil. Cut one of the pieces in half again. Cut one of those smaller pieces in half again. Continue cutting, making smaller and smaller pieces of aluminum foil. It should be obvious that the pieces are still aluminum foil; they are just becoming smaller and smaller. But how far can this exercise be taken, at least in theory? Can one continue cutting the aluminum foil into halves forever, making smaller and smaller pieces? Or is there some limit, some absolute smallest piece of aluminum foil? Thought experiments like this—and the conclusions based on them—were debated as far back as the fifth century BC.
John Dalton (1766-1844) is the scientist credited for proposing the atomic theory. The theory explains several concepts that are relevant in the observable world: the composition of a pure gold necklace, what makes the pure gold necklace different than a pure silver necklace, and what occurs when pure gold is mixed with pure copper. This section explains the theories that Dalton used as a basis for his theory: (1) Law of Conservation of Mass (2) Law of Definite Proportions, and (3) Law of Multiple Proportions
Law 1: The Conservation of Mass
"Nothing comes from nothing" is an important idea in ancient Greek philosophy that argues that what exists now has always existed, since no new matter can come into existence where there was none before. Antoine Lavoisier (1743-1794) restated this principle for chemistry with the law of conservation of mass, which "means that the atoms of an object cannot be created or destroyed, but can be moved around and be changed into different particles." This law says that when a chemical reaction rearranges atoms into a new product, the mass of the reactants (chemicals before the chemical reaction) is the same as the mass of the products (the new chemicals made). More simply, whatever you do, you will still have the same amount of stuff (however, certain nuclear reactions like fusion and fission can convert a small part of the mass into energy.
The law of conservation of mass states that the total mass present before a chemical reaction is the same as the total mass present after the chemical reaction; in other words, mass is conserved. The law of conservation of mass was formulated by Lavoisier as a result of his combustion experiment, in which he observed that the mass of his original substance—a glass vessel, tin, and air—was equal to the mass of the produced substance—the glass vessel, “tin calx”, and the remaining air.

Historically, this was a difficult concept for scientists to grasp. If this law was true, then how could a large piece of wood be reduced to a small pile of ashes? The wood clearly has a greater mass than the ashes. From this observation scientists concluded that mass had been lost. However, Figure \(\PageIndex{1}\) shows that the burning of word does follow the law of conservation of mass. Scientists did not account for the gases that play a critical role in this reaction.
The law of conservation of mass states that the total mass present before a chemical reaction is the same as the total mass present after the chemical reaction.
Law 2: Definite Proportions
Joseph Proust (1754-1826) formulated the law of definite proportions (also called the Law of Constant Composition or Proust's Law). This law states that if a compound is broken down into its constituent elements, the masses of the constituents will always have the same proportions, regardless of the quantity or source of the original substance. Joseph Proust based this law primarily on his experiments with basic copper carbonate. The illustration below depicts this law in action.
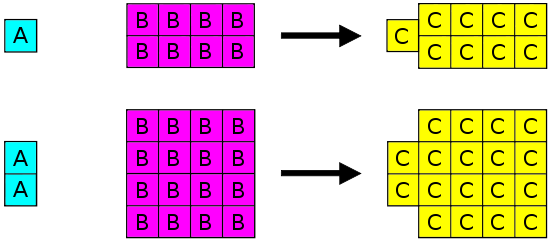
Law of Definite Proportions states that in a given type of chemical substance, the elements are always combined in the same proportions by mass.
The Law of Definite Proportions applies when elements are reacted together to form the same product. Therefore, while the Law of Definite Proportions can be used to compare two experiments in which hydrogen and oxygen react to form water, the Law of Definite Proportions can not be used to compare one experiment in which hydrogen and oxygen react to form water, and another experiment in which hydrogen and oxygen react to form hydrogen peroxide (peroxide is another material that can be made from hydrogen and oxygen).
Example \(\PageIndex{1}\): water
Oxygen makes up 88.8% of the mass of any sample of pure water, while hydrogen makes up the remaining 11.2% of the mass. You can get water by melting ice or snow, by condensing steam, from river, sea, pond, etc. It can be from different places: USA, UK, Australia, or anywhere. It can be made by chemical reactions like burning hydrogen in oxygen.
However, if the water is pure, it will always consist of 88.8 % oxygen by mass and 11.2 % hydrogen by mass, irrespective of its source or method of preparation.
Law 3: Multiple Proportions
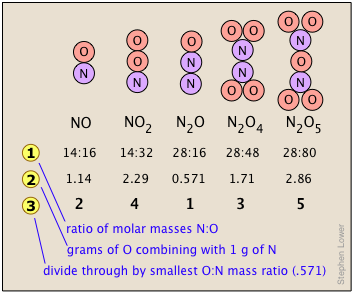
Many combinations of elements can react to form more than one compound. In such cases, this law states that the weights of one element that combine with a fixed weight of another of these elements are integer multiples of one another. It's easy to say this, but please make sure that you understand how it works. Nitrogen forms a very large number of oxides, five of which are shown here.
- Line
 shows the ratio of the relative weights of the two elements in each compound. These ratios were calculated by simply taking the molar mass of each element, and multiplying by the number of atoms of that element per mole of the compound. Thus for NO2, we have (1 × 14) : (2 × 16) = 13:32. (These numbers were not known in the early days of Chemistry because atomic weights (i.e., molar masses) of most elements were not reliably known.)
shows the ratio of the relative weights of the two elements in each compound. These ratios were calculated by simply taking the molar mass of each element, and multiplying by the number of atoms of that element per mole of the compound. Thus for NO2, we have (1 × 14) : (2 × 16) = 13:32. (These numbers were not known in the early days of Chemistry because atomic weights (i.e., molar masses) of most elements were not reliably known.) - The numbers in Line
 are just the mass ratios of O:N, found by dividing the corresponding ratios in line 1. But someone who depends solely on experiment would work these out by finding the mass of O that combines with unit mass (1 g) of nitrogen.
are just the mass ratios of O:N, found by dividing the corresponding ratios in line 1. But someone who depends solely on experiment would work these out by finding the mass of O that combines with unit mass (1 g) of nitrogen. - Line is obtained by dividing the figures the previous line by the smallest O:N ratio in the line above, which is the one for N2O. Note that just as the law of multiple proportions says, the weight of oxygen that combines with unit weight of nitrogen work out to small integers.
- Of course we just as easily could have illustrated the law by considering the mass of nitrogen that combines with one gram of oxygen; it works both ways!
The law of multiple proportions states that if two elements form more than one compound between them, the masses of one element combined with a fixed mass of the second element form in ratios of small integers.
Example \(\PageIndex{2}\): Oxides of Carbon
Consider two separate compounds are formed by only carbon and oxygen. The first compound contains 42.9% carbon and 57.1% oxygen (by mass) and the second compound contains 27.3% carbon and 72.7% oxygen (again by mass). Is this consistent with the law of multiple proportions?
Solution
The Law of Multiple Proportions states that the masses of one element which combine with a fixed mass of the second element are in a ratio of whole numbers. Hence, the masses of oxygen in the two compounds that combine with a fixed mass of carbon should be in a whole-number ratio.
Thus for every 1 g of the first compound there are 0.57 g of oxygen and 0.429 g of carbon. The mass of oxygen per gram carbon is:
\[ \dfrac{0.571\;g\; oxygen}{0.429 \;g \;carbon} = 1.33\; \dfrac{g oxygen}{g carbon} \nonumber\]
Similarly, for 1 g of the second compound, there are 0.727 g oxygen and 0.273 g of carbon. The ration of mass of oxygen per gram of carbon is
\[ \dfrac{0.727\;g\; oxygen}{0.273 \;g \;carbon} = 2.66\; \dfrac{g oxygen}{g carbon} \nonumber\]
Dividing the mass of oxygen per g of carbon of the second compound:
\[\dfrac{2.66}{1.33} = 2 \nonumber\]
Hence the masses of oxygen combine with carbon in a 2:1 ratio which s consistent with the Law of Multiple Proportions since they are whole numbers.
Dalton's Atomic Theory
The modern atomic theory, proposed about 1803 by the English chemist John Dalton (Figure \(\PageIndex{4}\)), is a fundamental concept that states that all elements are composed of atoms. Previously, an atom was defined as the smallest part of an element that maintains the identity of that element. Individual atoms are extremely small; even the largest atom has an approximate diameter of only 5.4 × 10−10 m. With that size, it takes over 18 million of these atoms, lined up side by side, to equal the width of the human pinkie (about 1 cm).

Dalton’s ideas are called the modern atomic theory because the concept of atoms is very old. The Greek philosophers Leucippus and Democritus originally introduced atomic concepts in the fifth century BC. (The word atom comes from the Greek word atomos, which means “indivisible” or “uncuttable.”) Dalton had something that the ancient Greek philosophers didn’t have, however; he had experimental evidence, such as the formulas of simple chemicals and the behavior of gases. In the 150 years or so before Dalton, natural philosophy had been maturing into modern science, and the scientific method was being used to study nature. When Dalton announced a modern atomic theory, he was proposing a fundamental theory to describe many previous observations of the natural world; he was not just participating in a philosophical discussion.
Dalton's Theory was a powerful development as it explained the three laws of chemical combination (above) and recognized a workable distinction between the fundamental particle of an element (atom) and that of a compound (molecule). Six postulates are involved in Dalton's Atomic Theory:
- All matter consists of indivisible particles called atoms.
- Atoms of the same element are similar in shape and mass, but differ from the atoms of other elements.
- Atoms cannot be created or destroyed.
- Atoms of different elements may combine with each other in a fixed, simple, whole number ratios to form compound atoms.
- Atoms of same element can combine in more than one ratio to form two or more compounds.
- The atom is the smallest unit of matter that can take part in a chemical reaction.
In light of the current state of knowledge in the field of Chemistry, Dalton’s theory had a few drawbacks. According to Dalton’s postulates,
- The indivisibility of an atom was proved wrong: an atom can be further subdivided into protons, neutrons and electrons. However an atom is the smallest particle that takes part in chemical reactions.
- According to Dalton, the atoms of same element are similar in all respects. However, atoms of some elements vary in their masses and densities. These atoms of different masses are called isotopes. For example, chlorine has two isotopes with mass numbers 35 and 37.
- Dalton also claimed that atoms of different elements are different in all respects. This has been proven wrong in certain cases: argon and calcium atoms each have an same atomic mass (40 amu).
- According to Dalton, atoms of different elements combine in simple whole number ratios to form compounds. This is not observed in complex organic compounds like sugar (\(C_{12}H_{22}O_{11}\)).
- The theory fails to explain the existence of allotropes (different forms of pure elements); it does not account for differences in properties of charcoal, graphite, diamond.
Despite these drawbacks, the importance of Dalton’s theory should not be underestimated. He displayed exceptional insight into the nature of matter. and his ideas provided a framework that was later modified and expanded by other. Consequentiually, John Dalton is often considered to be the father of modern atomic theory.
References
- Petrucci, Ralph, William Harwood, Geoffrey Herring, and Jeffry Madura. General Chemistry. 9th ed. Upper Saddle River, New Jersey: Pearson Prentince Hall, 2007
- Moore, John. Chemistry for Dummies. John Wiley & Sons Inc, 2002.
- Asimov, Isaac. A Short History of Chemistry. , CT.: Greenwood Press, 1965.
- Patterson, Elizabeth C. John Dalton and the Atomic Theory. Garden City, NY: Doubleday, 1970
- Myers, Richard. The Basics of Chemistry. Greenwood, 2003
- Demtröder, Wolfgang. Atoms, Molecules and Photons: An Introduction to Atomic- Molecular- and Quantum Physics. 1st ed. Springer. 2002
Summary
This article explains the theories that Dalton used as a basis for his theory: (1) the Law of Conservation of Mass, (2) the Law of Constant Composition, (3) the Law of Multiple Proportions.

