2.6: Ionic Compounds
- Page ID
- 58800
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Outcomes
- Describe the types of elements that form an ionic bond.
- Explain how an ionic bond is formed.
- Predict the formula of an ionic compound.
Chemistry can be broadly divided into tow main classes based on the identity of the elements present in the chemical compounds. Organic chemistry is the branch of chemistry that deals with compounds containing carbon. In this section and the following one, we will be discussing inorganic chemistry, which is the branch of chemistry dealing with compounds that do not contain carbon. Ionic compounds are examples of inorganic compounds.
Types of Formulas
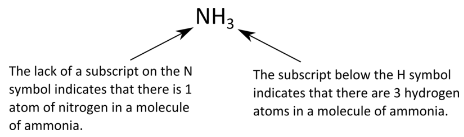
Recall that a molecules includes two or more atoms that have been chemically combined. A chemical formula that indicates how many of each type of atom are present in a single molecule is referred to as a molecular formula. For example, a molecule of ammonia contains one nitrogen atom and three hydrogen atoms, so it has the following molecular formula.
Another type of chemical formula, the empirical formula, shows the elements in a compound in their lowest whole-number ratio. Glucose is an important simple sugar that cells use as their primary source of energy. Its molecular formula is \(\ce{C_6H_{12}O_6}\). Since each of the subscripts is divisible by 6, the empirical formula for glucose is \(\ce{CH_2O}\). When chemists analyze an unknown compound, often the first step is to determine its empirical formula. There are a great many compounds whose molecular and empirical formulas are the same. If the molecular formula cannot be simplified into a smaller whole-number ratio, as in the case of \(\ce{H_2O}\) or \(\ce{P_2O_5}\), then the empirical formula is also the molecular formula.
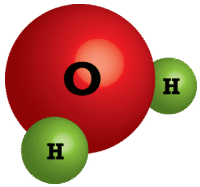
Unlike molecular compounds, ionic compounds are quite different. Water and other molecules exist as collections of individual molecules (see figure below) while ionic compounds do not exist as discrete molecular units. Instead,an ionic compound consists of a large three-dimensional array of alternating cations and anions. For example, sodium chloride \(\left( \ce{NaCl} \right)\) is composed of many \(\ce{Na^+}\) and \(\ce{Cl^-}\) ions arranged into a structure like the one pictured (see figure below). The formula for ionic compounds is always an empirical formula because it shows the smallest, whole-number ratio between the cations and anions. The actual number of ions in a sample of an ionic compound will be very large and will vary from sample to sample.
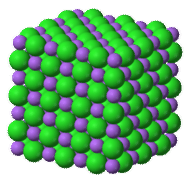
The most straightforward way to describe this structure with a chemical formula is to give the lowest whole-number ratio between the two ions. In the case of \(\ce{NaCl}\), there are equal numbers of sodium ions and chloride ions in the salt crystal. In contrast, a crystal of magnesium chloride has twice as many chloride ions as magnesium ions, so it has a formula of \(\ce{MgCl_2}\).
Writing Formulas for Binary Ionic Compounds
If you know the elements that form a binary ionic compound, you can write its formula. Start by writing the metal ion and its charge, followed by the nonmetal ion with its charge. Because the overall compound must be electrically neutral, decide how many ions of each type are needed in order for the positive and negative charges to cancel each other out. Consider the compound aluminum nitride. The charges on each of these ions can be determined by looking at the groups in which aluminum and nitrogen are found on the periodic table. The ions are:
\[\ce{Al^{3+}} \: \: \: \: \: \: \: \: \: \: \ce{N^{3-}}\]
Since the ions have charges that are equal in magnitude (3, but different signs), 1:1 is the lowest ratio of ions that will produce a neutral compound. Since the charge on aluminum is 3+ and the charge on nitrogen is \(3-\), the sum of their charges is zero (\(+3\;+\; -3=0\)). As a result, the formula of aluminum nitride is \(\ce{AlN}\). Another compound, lithium oxide, contains the following ions:
\[\ce{Li^+} \: \: \: \: \: \: \: \: \: \: \ce{O^{2-}}\]
In this case, two lithium ions, each with a 1+ charge, are required to balance out the charge of each oxide ion, which has a \(2-\) charge. The formula of lithium oxide is \(\ce{Li_2O}\) because the compound must be neutral. Therefore, \(\left( 2\times+1\right) \;+\left( 1\times -2\right)=0\).
For compounds in which the ratio of ions is not as obvious, an alternative way to determine the correct formula is to use the "crisscross" method. In this method, the numerical value of each charge crosses over to become the subscript of the opposite ion. The signs of the charges are dropped. The crisscross method is demonstrated below for aluminum oxide.
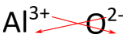
The red arrows indicate that the 3 from the \(3+\) charge will cross over to become the subscript for \(\ce{O}\), while the 2 from the \(2-\) charge will cross over to become the subscript for \(\ce{Al}\). The formula for aluminum oxide is \(\ce{Al_2O_3}\).
For aluminum oxide, the crisscross method directly produces the correct formula, but in some cases, another step is required. Because ionic compounds are always described by their empirical formulas, they must be written as the lowest whole-number ratio of the ions. In the case of aluminum nitride, the crisscross method would yield a formula of \(\ce{Al_3N_3}\), which is not correct. A second step must be performed in which the subscripts are reduced but the ratio is kept the same. \(\ce{Al_3N_3}\) can be reduced to \(\ce{AlN}\), because both formulas describe a 1:1 ratio of aluminum ions to nitride ions. Following the crisscross method to write the formula for lead (IV) oxide would involve the following steps:
Some transition metals can have more than one possible charge. When this happens, the charge on the transition metal cation is included in parentheses in the name. For example, lead(IV) oxide has \(\ce{Pb^{4+}}\) as its metal cation.
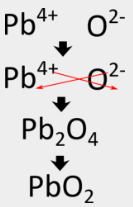
The crisscross method first yields \(\ce{Pb_2O_4}\) for the formula, but that must be reduced to \(\ce{PbO_2}\), which is the correct formula.
Writing Formulas for Ionic Compounds Containing Polyatomic Ions
Writing a formula for an ionic compound with polyatomic ions involves the same steps as for a binary (two element) ionic compound. Write the symbol and charge of the cation followed by the symbol and charge of the anion. Use the crisscross method to ensure that the final formula is neutral. Calcium nitrate is composed of calcium cations and nitrate anions.
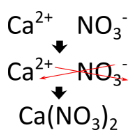
The charge is balanced by the presence of two nitrate ions and one calcium ion. Parentheses are used around the nitrate ion because more than one polyatomic ion is needed. If only one polyatomic ion is present in a formula, parentheses are not used. For example, the formula for calcium carbonate is \(\ce{CaCO_3}\). The carbonate ion carries a \(2-\) charge, so it exactly balances the \(2+\) charge of the calcium ion and parentheses are not needed around the polyatomic ion.
Example \(\PageIndex{1}\)
Write the formula for zinc phosphate which is composed of \(Zn^{2+}\) and \(PO_4^{3-}\) ions.
Solution
Write the metal cation followed by the nonmetal anion. Crisscross the ion charges in order to make the ionic compound neutral. Use parentheses around the polyatomic ion if more than one is present in the final formula. Reduce to the lowest ratio if necessary.
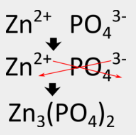
The formula for zinc phosphate is \(\ce{Zn_3(PO_4)_2}\). Three zinc cations with \(2+\) charges balance out two phosphate anions with \(3-\) charges.
Contributors and Attributions
Allison Soult, Ph.D. (Department of Chemistry, University of Kentucky)

