3.12: Substituted Cycloalkanes

Objectives

After completing this section, you should be able to

1. Draw the chair conformation of cyclohexane, with axial and equatorial hydrogen atoms clearly shown and identified.
2. identify the axial and equatorial hydrogens in a given sketch of the cyclohexane molecule.
3. explain how chair conformations of cyclohexane and its derivatives can interconvert through the process of ring flip.
4. account for the greater stability of the equatorial conformers of monosubstituted cyclohexanes compared to their axial counterparts, using the concept of 1,3‑diaxial interaction.
5. compare the gauche interactions in butane with the 1,3‑diaxial interactions in the axial conformer of methylcyclohexane.
6. arrange a given list of substituents in increasing or decreasing order of 1,3‑diaxial interactions.

Key Terms

Make certain that you can define, and use in context, the key terms below.

• axial position
• equatorial position
• ring flip
• 1,3‑diaxial interaction

Study Notes

1,3-Diaxial interactions are steric interactions between an axial substituent located on carbon atom 1 of a cyclohexane ring and the hydrogen atoms (or other substituents) located on carbon atoms 3 and 5.

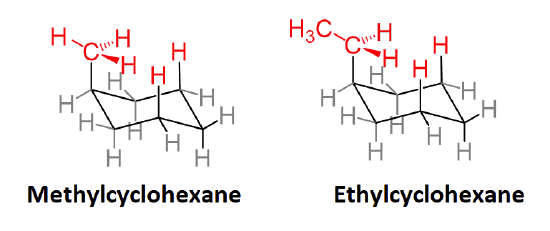
Be prepared to draw Newman-type projections for cyclohexane derivatives as the one shown for methylcyclohexane. Note that this is similar to the Newman projections from chapter 3 such as n-butane.

Newman projections of methylcyclohexane and n‑butane

 

Axial and Equatorial Positions in Cyclohexane

Careful examination of the chair conformation of cyclohexane, shows that the twelve hydrogens are not structurally equivalent. Six of them are located about the periphery of the carbon ring, and are termed equatorial. The other six are oriented above and below the approximate plane of the ring (three in each location), and are termed axial because they are aligned parallel to the symmetry axis of the ring.

In the figure above, the equatorial hydrogens are colored blue, and the axial hydrogens are black. Since there are two equivalent chair conformations of cyclohexane in rapid equilibrium, all twelve hydrogens have 50% equatorial and 50% axial character. 

 

How To Draw Axial and Equatorial Bonds

How not to draw the chair:

Aside from drawing the basic chair, the key points are:

• Axial bonds alternate up and down, and are shown "vertical".
• Equatorial groups are approximately horizontal, but actually somewhat distorted from that (slightly up or slightly down), so that the angle from the axial group is a bit more than a right angle -- reflecting the common 109.5^o bond angle.
• Each carbon has an axial and an equatorial bond.
• Each face of the cyclohexane ring has three axial and three equatorial bonds.
• Each face alternates between axial and equatorial bonds. Then looking at the "up" bond on each carbon in the cyclohexane ring they will alternate axial-equatorial-axial ect.
• When looking down at a cyclohexane ring:
  • the equatorial bonds will form an "equator" around the ring. 
  • The axial bonds will either face towards you or away. These will alternate with each axial bond. The first axial bond will be coming towards with the next going away.  There will be three of each type.
• Note! The terms cis and trans in regards to the stereochemistry of a ring are not directly linked to the terms axial and equatorial. It is very common to confuse the two.  It typically best not to try and directly inter convert the two naming systems.

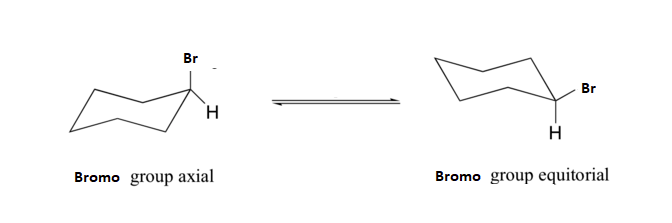
Axial vs. Equatorial Substituents

When a substituent is added to cyclohexane, the ring flip allows for two distinctly different conformations.  One will have the substituent in the axial position while the other will have the substituent in the equatorial position.  In the next section will discuss the energy differences between these two possible conformations.  Below are the two possible chair conformations of methylcyclohexane created by a ring-flip.  Although the conformation which places the methyl group in the equatorial position is more stable by 7 kJ/mol, the energy provided by ambient temperature allows the two conformations to rapidly interconvert. 

The figure below illustrates how to convert a molecular model of cyclohexane between two different chair conformations - this is something that you should practice with models. Notice that a 'ring flip' causes equatorial groups to become axial, and vice-versa.

Example \(\PageIndex{1}\)

For the following please indicate if the substituents are in the axial or equatorial positions.

Solution

Due to the large number of bonds in cyclohexane it is common to only draw in the relevant ones (leaving off the hydrogens unless they are involved in a reaction or are important for analysis). It is still possible to determine axial and equatorial positioning with some thought.  With problems such as this it is important to remember that each carbon in a cyclohexane ring has one axial and one equatorial bond.  Also, remember that axial bonds are perpendicular with the ring and appear to be going either straight up or straight down. Equatorial bonds will be roughly in the plane of the cyclohexane ring (only slightly up or down). Sometimes it is valuable to draw in the additional bonds on the carbons of interest.

With this it can be concluded that the bromine and chlorine substituents are attached in equatorial positions and the CH₃ substituent is attached in an axial position.

Monosubstituted Cyclohexanes

When a substituent is added to a cyclohexane ring, the two possible chair conformations created during a ring flip are not equally stable. In the example of methylcyclohexane the conformation where the methyl group is in the equatorial position is more stable than the axial conformation by 7.6 kJ/mol at 25^o C. The percentages of the two different conformations at equilibrium can be determined by solving the following equation for K (the equilibrium constant): ΔE = -RTlnK. In this equation ΔE is the energy difference between the two conformations, R is the gas constant (8.314 J/mol•K), T is the temperature in Kelvin, and K is the equilibrium constant for the ring flip conversion.  Using this equation, we can calculate a K value of 21 which means about 95% methylcyclohexane molecules have the methyl group in the equatorial position at 25^o C.

The energy difference between the two conformations comes from strain, called 1,3-diaxial interactions, created when the axial methyl group experiences steric crowding with the two axial hydrogens located on the same side of the cyclohexane ring. Because axial bonds are parallel to each other, substituents larger than hydrogen experience greater steric crowding when they are oriented axial rather than equatorial. Consequently, substituted cyclohexanes will preferentially adopt conformations in which the larger substituents are in the equatorial orientation. When the methyl group is in the equatorial position this strain is not present which makes the equatorial conformer more stable and favored in the ring flip equilibrium. 

Actually, 1,3-diaxial steric strain is directly related to the steric strain created in the gauche conformer of butane discussed in Section: 3-7.  When butane is in the gauche conformation 3.8 kJ/mol of strain was created due the steric crowding of two methyl group with a 60^o dihedral angle. When looking at the a Newman projection of axial methylcyclohexane the methyl group is at a 60^o dihedral angle with the ring carbon in the rear.  This creates roughly the same amount of steric strain as the gauche conformer of butante.  Given that there is actually two such interactions in axial methylcyclohexane, it makes sense that there is 2(3.8 kJ/mol) = 7.6 kJ/mol of steric strain in this conformation.  The Newman projection of equatorial methylcyclohexane shows no such interactions and is therefore more stable. 
 

Newman projections of methyl cyclohexane and butane showing similarity of 1,3-diaxial and gauche interactions.

 

Strain values for other cyclohexane substituents can also be considered. The relative steric hindrance experienced by different substituent groups oriented in an axial versus equatorial location on cyclohexane determined the amount of strain generated. The strain generated can be used to evaluate the relative tendency of substituents to exist in an equatorial or axial location. Looking at the energy values in this table, it is clear that as the size of the substituent increases, the 1,3-diaxial energy tends to increase, also. Note that it is the size and not the molecular weight of the group that is important. Table 4.7.1 summarizes some of these strain values values.

 

Table 4.7.1: A Selection of ΔG° Values for the Change from Axial to Equatorial Orientation of Substituents for Monosubstituted Cyclohexanes

Substituent	-ΔG° (kcal/mol)	Substituent	-ΔG° (kcal/mol)
\(\ce{CH_3\bond{-}}\)	1.7	\(\ce{O_2N\bond{-}}\)	1.1
\(\ce{CH_2H_5\bond{-}}\)	1.8	\(\ce{N#C\bond{-}}\)	0.2
\(\ce{(CH_3)_2CH\bond{-}}\)	2.2	\(\ce{CH_3O\bond{-}}\)	0.5
\(\ce{(CH_3)_3C\bond{-}}\)	\(\geq 5.0\)	\(\ce{HO_2C\bond{-}}\)	0.7
\(\ce{F\bond{-}}\)	0.3	\(\ce{H_2C=CH\bond{-}}\)	1.3
\(\ce{Cl\bond{-}}\)	0.5	\(\ce{C_6H_5\bond{-}}\)	3.0
\(\ce{Br\bond{-}}\)	0.5
\(\ce{I\bond{-}}\)	0.5

Exercises

1) Draw two conformations of cyclohexyl amine (C₆H₁₁NH₂). Indicate axial and equatorial positions.

2) Draw the two isomers of 1,4-dihydroxylcyclohexane, identify which are equatorial and axial.

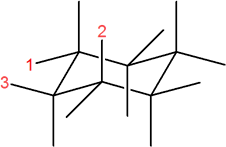
3) In the following molecule, label which are equatorial and which are axial, then draw the chair flip (showing labels 1,2,3).

Solutions

 

1)

2)

3) Original conformation: 1 = axial, 2 = equatorial, 3 = axial

Flipped chair now looks like this.

Exercises

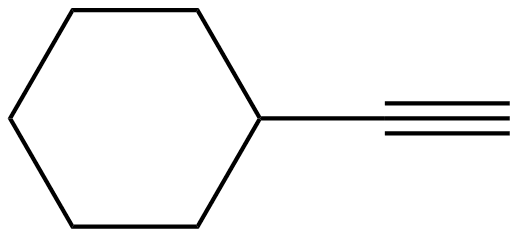
1) In the molecule, cyclohexyl ethyne there is little steric strain, why?

2) Calculate the energy difference between the axial and equatorial conformations of bromocyclohexane?

3) Using your answer from Question 2) estimate the percentages of axial and equatorial conformations of bromocyclohexane at 25^o C.

4) There very little in 1,3-diaxial strain when going from a methyl substituent (3.8 kJ/mol) to an ethyl substituent (4.0 kJ/mol), why? It may help to use molecular model to answer this question.

Solutions

1) The ethyne group is linear and therefore does not affect the hydrogens in the 1,3 positions to say to the extent as a bulkier or a bent group (e.g. ethene group) would. This leads to less of a strain on the molecule.

2) The equatorial conformation of bromocyclohexane will have two 1,3 diaxial interactions.  The table above states that each interaction accounts for 1.2 kJ/mol of strain.  The total strain in equatorial bromocyclohexane will be 2(1.2 kJ/mol) = 2.4 kJ/mol.

3) Remembering that the axial conformation is higher in energy, the energy difference between the two conformations is ΔE = (E equatorial - E axial) = (0 - 2.4 kJ/mol) = -2.4 kJ/mol.  After converting ^oC to Kelvin and kJ/mol to J/mol we can use the equation ΔE = -RT lnK to find that -ΔE/RT = lnK or (2.4 x 10³ J/mol) / (8.313 kJ/mol K • 298 K) = lnK. From this we calculate that K = 2.6. Because the ring flip reaction is an equilibrium we can say that K = [Equatorial] / [Axial].  If assumption is made that [Equatorial] = X then [Axial] must be 1-X.  Plugging these values into the equilibrium expression produces K = [X] / [1-X].  After plugging in the calculated value for K, X can be solved algebraically.  2.6 = [X] / [1-X] → 2.6 - 2.6X = X → 2.6 = 3.6X → 2.6/3.6 = X = 0.72.  This means that bromocyclohexane is in the equatorial position 72% of the time and in the axial position 28% of the time.

4) The fact that C-C sigma bonds can freely rotate allows the ethyl subsistent to obtain a conformation which places the bulky CH₃ group away from the cyclohexane ring.  This forces the ethyl substituent to have only have 1,3- diaxial interactions between hydrogens, which only provides a slight difference to a methyl group.

Contributors and Attributions

• Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)

• Prof. Steven Farmer (Sonoma State University)

• >Robert Bruner (http://bbruner.org)

• Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)

• Layne Morsch (University of Illinois Springfield)

• Dr. Krista Cunningham