6.10: Valence Bond Theory

Skills to Develop

• To describe the bonding in simple compounds using valence bond theory.

Although the VSEPR model is a simple and useful method for qualitatively predicting the structures of a wide range of compounds, it is not infallible. It predicts, for example, that H₂S and PH₃ should have structures similar to those of \(\ce{H2O}\) and \(\ce{NH3}\), respectively. In fact, structural studies have shown that the H–S–H and H–P–H angles are more than 12° smaller than the corresponding bond angles in \(\ce{H2O}\) and \(\ce{NH3}\), even though the electron groups should have more space around the larger atoms. More disturbing, the VSEPR model predicts that the simple group 2 halides (MX₂), which have four valence electrons, should all have linear X–M–X geometries. Instead, many of these species, including \(\ce{SrF2}\) and \(\ce{BaF2}\), are significantly bent. A more sophisticated treatment of bonding is needed for systems such as these. In this section, we present a quantum mechanical description of bonding, in which bonding electrons are viewed as being localized between the nuclei of the bonded atoms.

As we have talked about using Lewis structures to depict the bonding in covalent compounds, we have been very vague in our language about the actual nature of the chemical bonds themselves. We know that a covalent bond involves the ‘sharing’ of a pair of electrons between two atoms - but how does this happen, and how does it lead to the formation of a bond holding the two atoms together?

The valence bond theory is introduced to describe bonding in covalent molecules. In this model, bonds are considered to form from the overlapping of two atomic orbitals on different atoms, each orbital containing a single electron. In looking at simple inorganic molecules such as H₂ or HF, our present understanding of s and p atomic orbitals will suffice. To explain the bonding in organic molecules, however, we will need to introduce the concept of hybrid orbitals.

Valence Bond Theory: A Localized Bonding Approach

The simplest case to consider is the hydrogen molecule, H₂. When we say that the two electrons from each of the hydrogen atoms are shared to form a covalent bond between the two atoms, what we mean in valence bond theory terms is that the two spherical 1s orbitals overlap, allowing the two electrons to form a pair within the two overlapping orbitals. In simple terms, we can say that both electrons now spend more time between the two nuclei and thus hold the atoms together. As we will see, the situation is not quite so simple as that, because the electron pair must still obey quantum mechanics - that is, the two electrons must now occupy a shared orbital space. This will be the essential principle of valence bond theory.

You learned previously that as two hydrogen atoms approach each other from an infinite distance, the energy of the system reaches a minimum. This region of minimum energy in the energy diagram corresponds to the formation of a covalent bond between the two atoms at an H–H distance of 74 pm (Figure \(\PageIndex{1}\)). According to quantum mechanics, bonds form between atoms because their atomic orbitals overlap, with each region of overlap accommodating a maximum of two electrons with opposite spin, in accordance with the Pauli principle. In this case, a bond forms between the two hydrogen atoms when the singly occupied 1s atomic orbital of one hydrogen atom overlaps with the singly occupied 1s atomic orbital of a second hydrogen atom. Electron density between the nuclei is increased because of this orbital overlap and results in a localized electron-pair bond (Figure \(\PageIndex{1}\)).

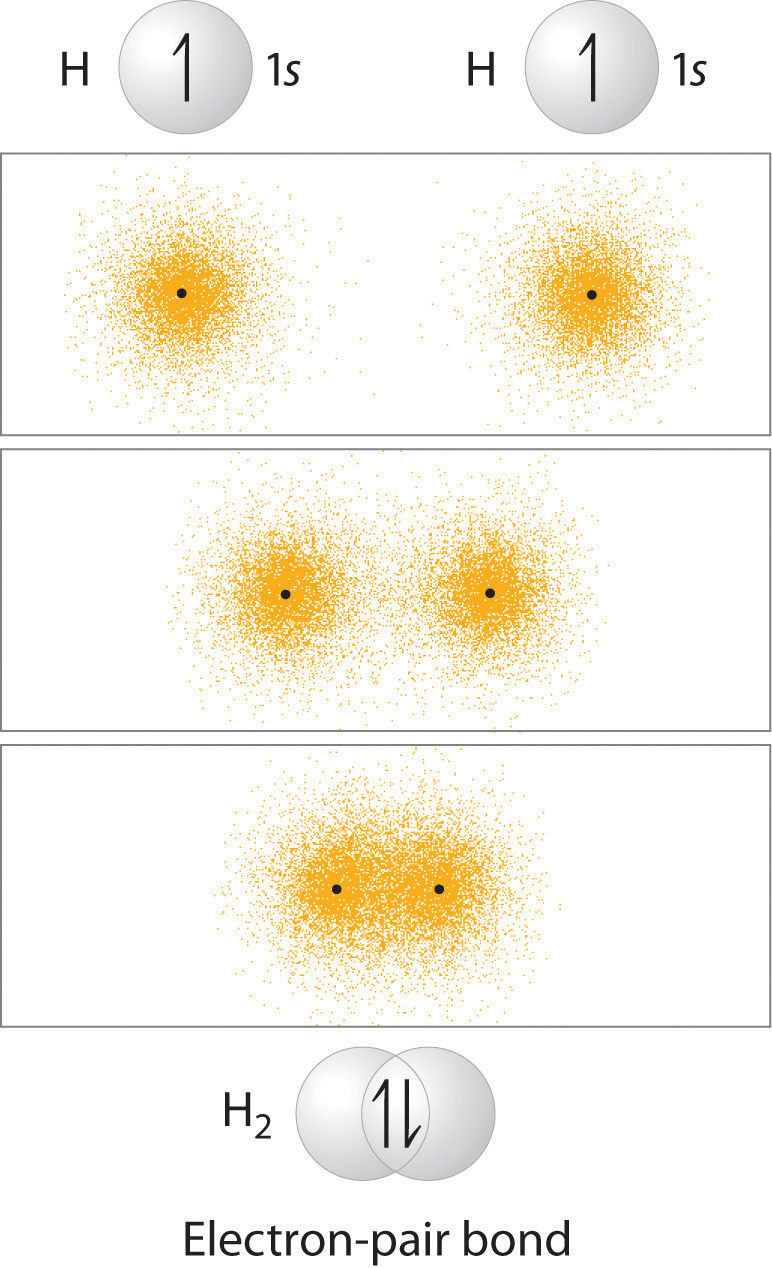
Figure \(\PageIndex{1}\): Overlap of Two Singly Occupied Hydrogen 1s Atomic Orbitals Produces an H–H Bond in H_2. The formation of H₂ from two hydrogen atoms, each with a single electron in a 1s orbital, occurs as the electrons are shared to form an electron-pair bond, as indicated schematically by the gray spheres and black arrows. The orange electron density distributions show that the formation of an H₂ molecule increases the electron density in the region between the two positively charged nuclei.

Although Lewis and VSEPR structures also contain localized electron-pair bonds, neither description uses an atomic orbital approach to predict the stability of the bond. Doing so forms the basis for valence bond theory, which is built on two assumptions:

1. The strength of a covalent bond is proportional to the amount of overlap between atomic orbitals; that is, the greater the overlap, the more stable the bond.
2. An atom can use different combinations of atomic orbitals to maximize the overlap of orbitals used by bonded atoms.

Maximum overlap occurs between orbitals with the same spatial orientation and similar energies.

Figure \(\PageIndex{2}\) shows an electron-pair bond formed by the overlap of two ns atomic orbitals, two np atomic orbitals, and an ns and an np orbital where n = 2. Notice that bonding overlap occurs when the interacting atomic orbitals overlap in phase (represented by colors in Figure \(\PageIndex{2}\) ).

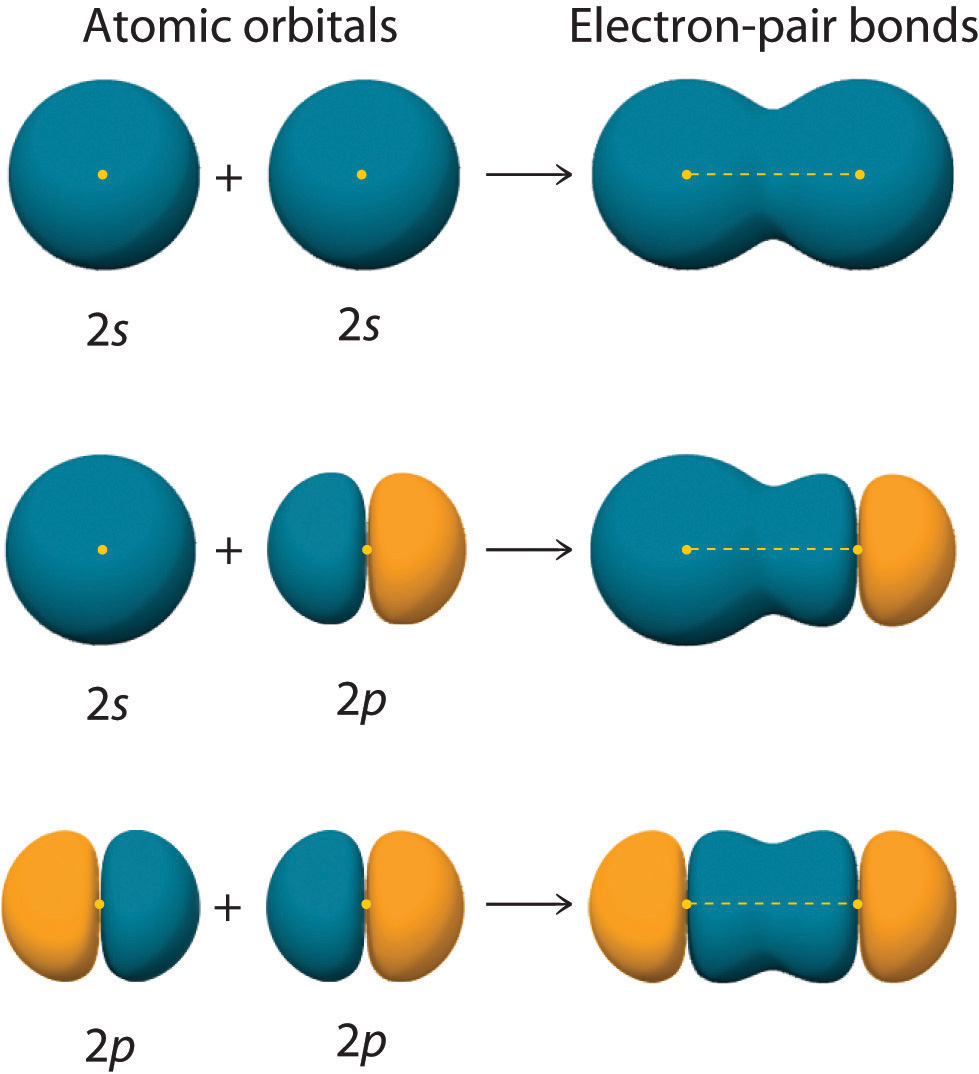
Figure \(\PageIndex{2}\) : Three Different Ways to Form an Electron-Pair Bond. An electron-pair bond can be formed by the overlap of any of the following combinations of two singly occupied atomic orbitals: two ns atomic orbitals (a), an ns and an np atomic orbital (b), and two np atomic orbitals (c) where n = 2. The positive lobe is indicated in yellow, and the negative lobe is in blue.

As another example, consider the Cl₂ molecule. The valence electron configuration of each Cl atom is 3s²3p⁵, with one p orbital containing only one electron. According to valence bond theory, the two half-filled p orbitals will overlap in an end-to-end fashion, as in Figure \(\PageIndex{2c}\), to contain a bonding electron pair. Thus, the Cl₂ molecule also contains a single bond comprised of two p orbitals.

Sigma and Pi Bonds

In addition to the distance between two orbitals, the orientation of orbitals also affects their overlap (other than for two s orbitals, which are spherically symmetric). Greater overlap is possible when orbitals are oriented such that they overlap on a direct line between the two nuclei. Figure \(\PageIndex{3}\) illustrates this for two p orbitals from different atoms; the overlap is greater when the orbitals overlap end to end rather than at an angle.

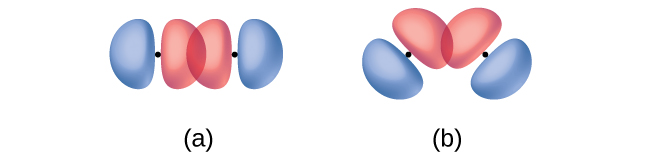
Figure \(\PageIndex{3}\): (a) The overlap of two p orbitals is greatest when the orbitals are directed end to end. (b) Any other arrangement results in less overlap. The dots indicate the locations of the nuclei.

The overlap of two s orbitals (as in H₂), the overlap of an s orbital and a p orbital (as in HCl), and the end-to-end overlap of two p orbitals (as in Cl₂) all produce sigma bonds (σ bonds), as illustrated in Figure \(\PageIndex{4}\). A σ bond is a covalent bond in which the electron density is concentrated in the region along the internuclear axis; that is, a line between the nuclei would pass through the center of the overlap region. Single bonds in Lewis structures are described as σ bonds in valence bond theory.

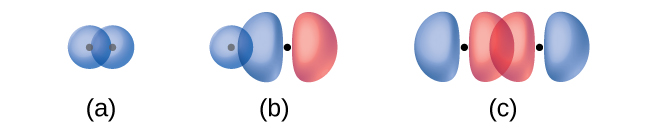
Figure \(\PageIndex{4}\): Sigma (σ) bonds form from the overlap of the following: (a) two s orbitals, (b) an s orbital and a p orbital, and (c) two p orbitals. The dots indicate the locations of the nuclei.

This is not the only way that p orbitals can interact with each other, however. A pi bond (π bond) is a type of covalent bond that results from the side-by-side overlap of two p orbitals, as illustrated in Figure \(\PageIndex{5}\). In a π bond, the regions of orbital overlap lie on opposite sides of the internuclear axis. Along the axis itself, there is a node, that is, a plane with no probability of finding an electron.

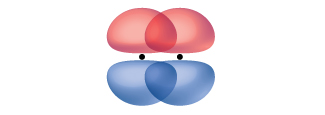
Figure \(\PageIndex{5}\): Pi (π) bonds form from the side-by-side overlap of two p orbitals. The dots indicate the location of the nuclei.

 

While all single bonds are σ bonds, multiple bonds consist of both σ and π bonds. As the Lewis structures suggest, O₂ contains a double bond, and N₂ contains a triple bond. The double bond consists of one σ bond and one π bond, and the triple bond consists of one σ bond and two π bonds. Between any two atoms, the first bond formed will always be a σ bond, but there can only be one σ bond in any one location. In any multiple bond, there will be one σ bond, and the remaining one or two bonds will be π bonds. These bonds are described in more detail later in this chapter.

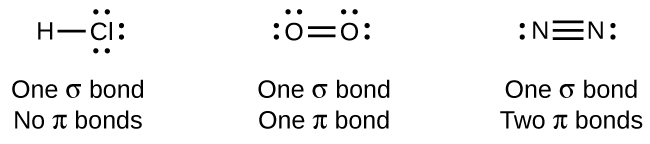
As seen in 6.2: Molecules and Bonds, an average carbon-carbon single bond is 347 kJ/mol, while in a carbon-carbon double bond, the π bond increases the bond strength by 267 kJ/mol. Adding an additional π bond causes a further increase of 225 kJ/mol. We can see a similar pattern when we compare other σ and π bonds. Thus, each individual π bond is generally weaker than a corresponding σ bond between the same two atoms. In a σ bond, there is a greater degree of orbital overlap than in a π bond.

Example \(\PageIndex{1}\): Counting σ and π Bonds

Butadiene, C₄H₆, is used to make synthetic rubber. Identify the number of σ and π bonds contained in this molecule.

Butadiene

Solution

There are six σ C–H bonds and one σ C–C bond, for a total of seven from the single bonds. There are two double bonds that each have a π bond in addition to the σ bond. This gives a total nine σ and two π bonds overall.

Exercise \(\PageIndex{1}\)

Identify each illustration as depicting a σ or π bond:

1. side-by-side overlap of a 4p and a 2p orbital
2. end-to-end overlap of a 4p and 4p orbital
3. end-to-end overlap of a 4p and a 2p orbital

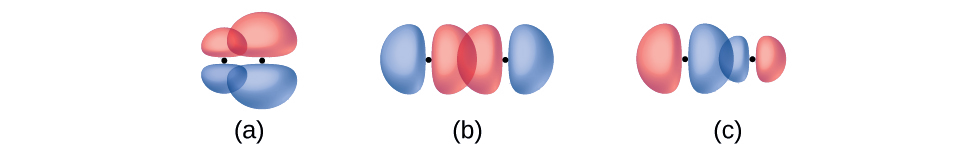
Answer

(a) is a π bond with a node along the axis connecting the nuclei while (b) and (c) are σ bonds that overlap along the axis.

 

 

Polyatomic Molecules

What about molecules containing more than two atoms? Let’s examine the bonds in BeH₂, for example. According to the VSEPR model, BeH₂ is a linear compound with four valence electrons and two Be–H bonds. Its bonding can also be described using an atomic orbital approach. Beryllium has a 1s²2s² electron configuration, and each H atom has a 1s¹ electron configuration. Because the Be atom has a filled 2s subshell, however, it has no singly occupied orbitals available to overlap with the singly occupied 1s orbitals on the H atoms. If a singly occupied 1s orbital on hydrogen were to overlap with a filled 2s orbital on beryllium, the resulting bonding orbital would contain three electrons, but the maximum allowed by quantum mechanics is two. How then is beryllium able to bond to two hydrogen atoms? One way would be to add enough energy to excite one of its 2s electrons into an empty 2p orbital and reverse its spin, in a process called promotion:

In this excited state, the Be atom would have two singly occupied atomic orbitals (the 2s and one of the 2p orbitals), each of which could overlap with a singly occupied 1s orbital of an H atom to form an electron-pair bond. Although this would produce \(\ce{BeH2}\), the two Be–H bonds would not be equivalent: the 1s orbital of one hydrogen atom would overlap with a Be 2s orbital, and the 1s orbital of the other hydrogen atom would overlap with an orbital of a different energy, a Be 2p orbital. Experimental evidence indicates, however, that the two Be–H bonds have identical energies. To resolve this discrepancy and explain how molecules such as \(\ce{BeH2}\) form, scientists developed the concept of hybridization, discussed in the next section.

 

Glossary

overlap

coexistence of orbitals from two different atoms sharing the same region of space, leading to the formation of a covalent bond

node

plane separating different lobes of orbitals, where the probability of finding an electron is zero

pi bond (π bond)

covalent bond formed by side-by-side overlap of atomic orbitals; the electron density is found on opposite sides of the internuclear axis

sigma bond (σ bond)

covalent bond formed by overlap of atomic orbitals along the internuclear axis

valence bond theory

description of bonding that involves atomic orbitals overlapping to form σ or π bonds, within which pairs of electrons are shared

Contributors 

• Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)

• Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).

• Anna Christianson (Bellarmine University)