Worksheet 4A: Introduction to the Quantum Harmonic Oscillator

Name: ______________________________

Section: _____________________________

Student ID#:__________________________

Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.

The Classical Harmonic Oscillator

In classical mechanics, a harmonic oscillator (HO) is a system that, when displaced from its equilibrium position (\(x_o\)), experiences a restoring force, \(F\), proportional to the displacement from equilibrium (\(x-x_o\)). For the 1-D HO, this force is given by

\[F(x)=-k(x -x_o) \label{eq1}\]

where \(k\) is a positive constant (often called a "spring constant"). Equation \ref{eq1} is often referred to as Hookes' Law with \(k\) called "Hooke's constant." The force in Equation \ref{eq1} is a conservative force since it dependents only on position. Hence, a potential energy \(V(x)\) can be constructed to describe this force

Equating Equations \ref{eq1} and \ref{eq2} and then integrating results in the following HO potential

\[V(x) = \dfrac{1}{2} k (x-x_o)^2 \label{eq3}\]

If \(F\) is the only force acting on the system, the system is called a simple (or undamped) harmonic oscillator, and undergoes simple harmonic motion: sinusoidal oscillations about the equilibrium point, with a constant amplitude and a constant frequency (which does not depend on the amplitude). This is demonstrated by solving the coresponding equations of motion (below).

Combining Newton's 2nd law of motion and Equation \ref{eq1} results in a 1D wave equation

\[{F=ma=m{\dfrac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=m{\ddot {x}}=-kx.} \label{eq4}\]

Solving this 2nd order differential equation, we find that the motion is described by the function

\[x(t)=A\cos(\omega t+\varphi ) \label{eq5}\]

where

\[\omega =\sqrt {\dfrac {k}{m}}=\dfrac {2\pi }{T}. \label{eq6}\]

The motion is periodic, repeating itself in a sinusoidal fashion with constant amplitude, \(A\) with a period \(T\). This motion can be viewed as a particle moving along the HO potential \(V(x)\) or alternatively, as motion of a mass on a simple spring where \(k\) is a measure of the strength of the spring.

A mass connected to a spring that follows Hooke's law is a system that, when displaced from its equilibrium position, experiences a restoring force, \(F\) that is proportional to the displacement, \(x-x_o\).

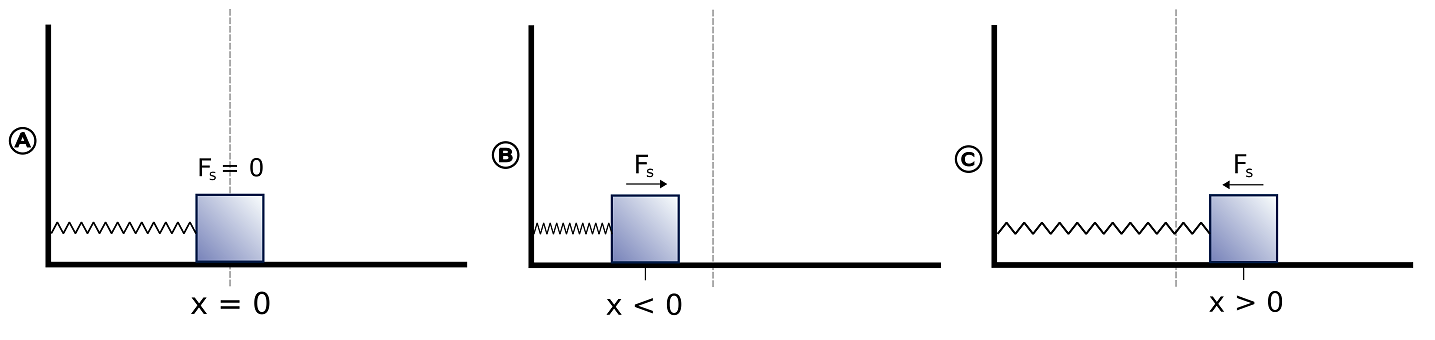
Q1

In the following plots, draw the different classical harmonic oscillator potentials with the given parameters (label the axes too).

1. \(V_1(x)\): \(x_o=0\) and \(k=0.5\)
2. \(V_2(x)\): \(x_o=2\) and \(k=0.25\)

Q2

1. What is the force exerted on a particle in each of the potentials in Q1 at \(x=-1\), \(x=0\) and \(x=+1\).
2. What will happen to this particle if it has no initial motion at these position?

Q3

For a particle moving in the classical HO potential, the motion will be oscillatory (Equation \ref{eq5}).

1. How does the frequency of this oscillation change if the mass of the particle doubles?
2. How does the frequency of this oscillation change if the spring constant doubles?

The Quantum Harmonic Oscillator

The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. It is one of the most important model systems in quantum mechanics and is one of the few quantum-mechanical systems for which an exact, analytical solution is known (as is the particle in a box discussed previously).

Q4

We can extend the classical HO to the quantum world by adopting the classical HO potential (Equation \ref{eq3}) into the Schrödinger equation. Write the corresponding time independent Schrödinger equation.

Solutions to the Quantum Harmonic Oscillator

A particle in a HO potential is trapped just like a particle in a box and similar intuition applies to both systems. While the Schrödinger equation in Q4 can be analytically solved, it is appreciably harder than solving the particle in a box model and is beyond the scope of most introductory quantum classes.

When solved, the eigenstates are

\[ \psi_v(x)= \dfrac {1}{\sqrt {2^v \,v!}} \cdot \left( \dfrac {m\omega }{\pi \hbar }\right)^{1/4} \cdot \exp \left(-\dfrac {m\omega x^2}{2\hbar }\right) \cdot H_{n} \left( \sqrt {\dfrac {m\omega }{\hbar }}x \right), \label{HO1}\]

with \(v=0,1,2,\ldots\).

where the functions \(H_n\) are the Hermite polynomials.

\[H_{v}(x)=(-1)^{v}~e^{x^{2}}{\frac {d^{v}}{dx^{v}}}\left(e^{-x^{2}}\right).\]

The corresponding energy levels are

\[ E_{v}=\hbar \omega \left(v+{1 \over 2}\right)\]

Q5

The quantum HO eigenstates can be decomposed into a three parts:

1. Identify the Gaussian component
2. Identify the Hermite polynomial component
3. Identify the normalization component

Q6

1. What is the zero point energy for the quantum HO? Does it surprise you that it is not zero?
2. How many eigenstates does the quantum HO have?
3. What are the limits of the quantum HO quantum number and how does it differ from the limits of the quantum number for the particle in a box?

Q7

What are the boundary conditions (better thought of as expectations for the solutions) for solving the quantum HO?

Q8

The first two Hermite polynomials are \(H_0=1\) and \(H_1=2x\). From this information and Equation \ref{HO1}, draw the ground-state and first excited-state eigenstates for the quatum HO. Draw the corresponding potential used to generate these eigenstates.

Q9

1. How many nodes are in the two eigenstates drawn in Q8?
2. From inspection of your plots, what is the average position (\(\langle x \rangle\)) for the particle in both eigenstates?

Q10

For a box of similar length (guesstimate it), draw the ground eigenstate and first excited eigenstate for the particle in a box over the corresponding boundary drawn in Q8. How do they differ and how do they resemble each other?