#8B Homework Solution: ab initio Calculations
- Page ID
- 109924
Name: ______________________________
Section: _____________________________
Student ID#:__________________________
This homework is a little different. We will use the cool web base ab initio site by Perri at Sonoma State U. Download the following paper and review the concept (http://pubs.acs.org/doi/pdf/10.1021/ed5004228). Follow the directions on this tutorial (you will not need to install Avogadro for this HW). We will use this package multiple times in this class so make sure you can complete the online tutorial if you are confused.
To start the calculations
- click here: https://chemcompute.org
- sign in: Username: "Chem110A" and password: "Halloween"
- click on GAMESS at the top
- click on "submit" on top right
We are going to calculate the binding energy of the first two row of atoms with the ChemCompute software. Before beginning, we need to discuss an advanced aspect of electronic wavefuctions: Spin. You know from your general chemistry class that electrons have a "spin" that is related to the \(m_s\) quantum number that can be either "up" with \(m_s = +1/2\) or "down" with \(m_s = -1/2\). Review your electron configuration rules (especially Hund's rules) if you are not familiar with this.
The multiplicity of an energy state is defined as \(2S+1\), where \(S\) is the total spin angular momentum and is determined by adding the \(m_s\) quantum numbers of all electrons in the system (atom or molecule):
\[S =\sum m_s\]
The spin multiplicity of the system will be discussed in detail later on in course. States with multiplicity 1, 2, 3, 4, 5 are respectively called singlets, doublets, triplets, quartets and quintets. The triplet state indicates that the multiplicity \(2S+1 = 3\), so that the total spin \(S = 1\). This spin is due to two unpaired electrons, as a result of Hund's rule which favors the single filling of degenerate orbitals.
For example, the electronic configuration of the ground state of the nitrogen atom is \(1s^22S^22P^3\) and has one electron in each of the 2p orbitals (each with the same spin so same \(m_s\) value, e.g., +1/2. So for this system
\[S = + 1/2 -1/2 +1/2 - 1/2 +1/2 + 1/2 +1/2 = 3/2\]
and the multiplicity is \(2 \times 3/2 +1 = 4\); the ground state nitrogen atom is a quartet state.
You will want to prepare the table below with the appropriate details before you do the quantum calculation.
Building the first Two rows of the Periodic Table
Run the single-point calculations on the first ten atoms of the periodic table (Hydrogen to Neon) and fill in the below table. You only need to extract the total energy of each system for the table, but you need to address the spin of the system explicitly (those are the rules of quantum calculations).
- If the spin multiplicity of the atom is not 1, then use the UHR (Unrestricted Hartree-Fock) method,
- If the spin multiplicity of the atom is 1, you can use either the RHF (Restricted Hartree-Fock) or UHR method (should give the same results).
Use the 6-311G** basis set for both. If you select the RHF and have a non-unity spin multiplicity, the program will give you an error.
Pull in the 03166 input file (job# 3166) to get the helium atom. The hydrogen atom is already done for you
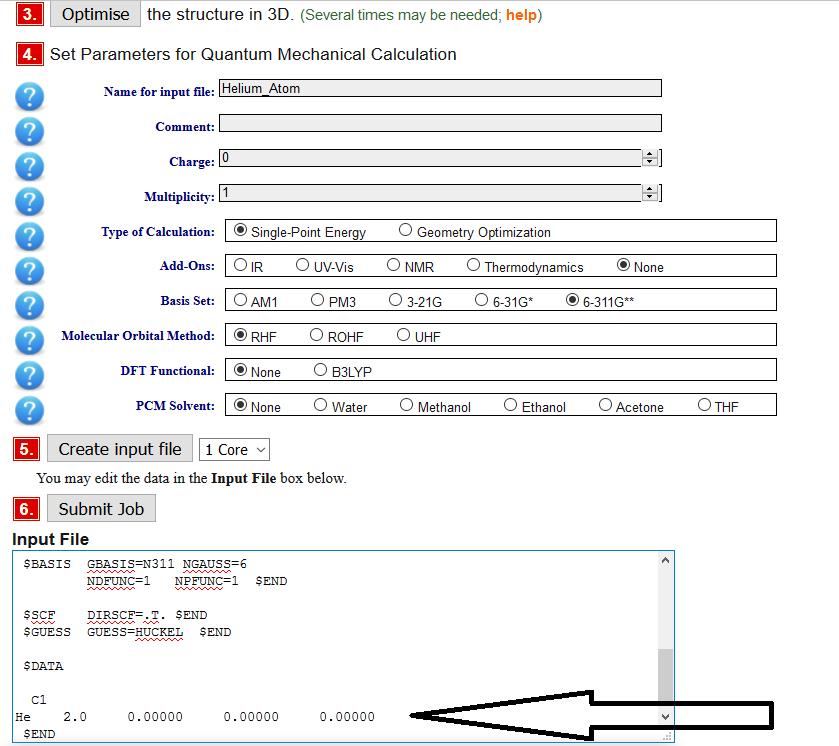
When you recalculate a new atom you will have to change the multiplicity for the molecule (from the table you are making below) and then you "create" the input file and swap to the next atom in the input (see arrow above) by changing these two things
- the name of the atom to the standard chemical abbreviation and
- the number after that is the atomic number \(Z\).
| Atom | Nuclear Charge (\(Z\)) | Number of Electrons \(n\) | Electronic Configuration | Total electron spin \(S = \sum m_s\) | Spin Multiplicity \(2S+1\) | Total Energy \(E_Z\) | \(n Z^2 E_{1} \) | \(Z_{eff}\) |
|---|---|---|---|---|---|---|---|---|
| Hydrogen | 1 | 1 | \(1s^1\) | 1/2 | 2 | 313 | 313 | 1 |
| Helium | 2 | 2 | \(1s^2\) | 0 | 1 | 1794 | 2504 | 1.692872 |
| Lithium | 3 | 3 | \(1s^22s^1\) | 1/2 | 2 | 4663 | 8451 | 2.30594 |
| Beryllium | 4 | 4 | \(1s^22s^2\) | 0 | 1 | 9143 | 20032 | 2.702354 |
| Boron | 5 | 5 | \(1s^22s^22p^1\) | 1/2 | 2 | 15392 | 39125 | 3.136103 |
| Carbon | 6 | 6 | \(1s^22s^22p^2\) | 1 | 3 | 23650 | 67608 | 3.548688 |
| Nitrogen | 7 | 7 | \(1s^22s^22p^3\) | 3/2 | 4 | 34135 | 107359 | 3.947106 |
| Oxygen | 8 | 8 | \(1s^22s^22p^4\) | 1 | 3 | 46940 | 160256 | 4.329666 |
| Fluorine | 9 | 9 | \(1s^22s^22p^5\) | 1/2 | 2 | 62371 | 228177 | 4.705415 |
| Neon | 10 | 10 | \(1s^22s^22p^6\) | 0 | 1 | 80648 | 313000 | 5.076035 |
To be Submitted for Credit
It is VERY useful to review these two pages to interpret your results for credit.
- http://chem.libretexts.org/Under_Con...rons_and_Light
- http://chem.libretexts.org/LibreText...Slater's_Rules
- Submit the above table filled out for the total binding electronic energy of each atom (do not copy from others as if we will compare tables)
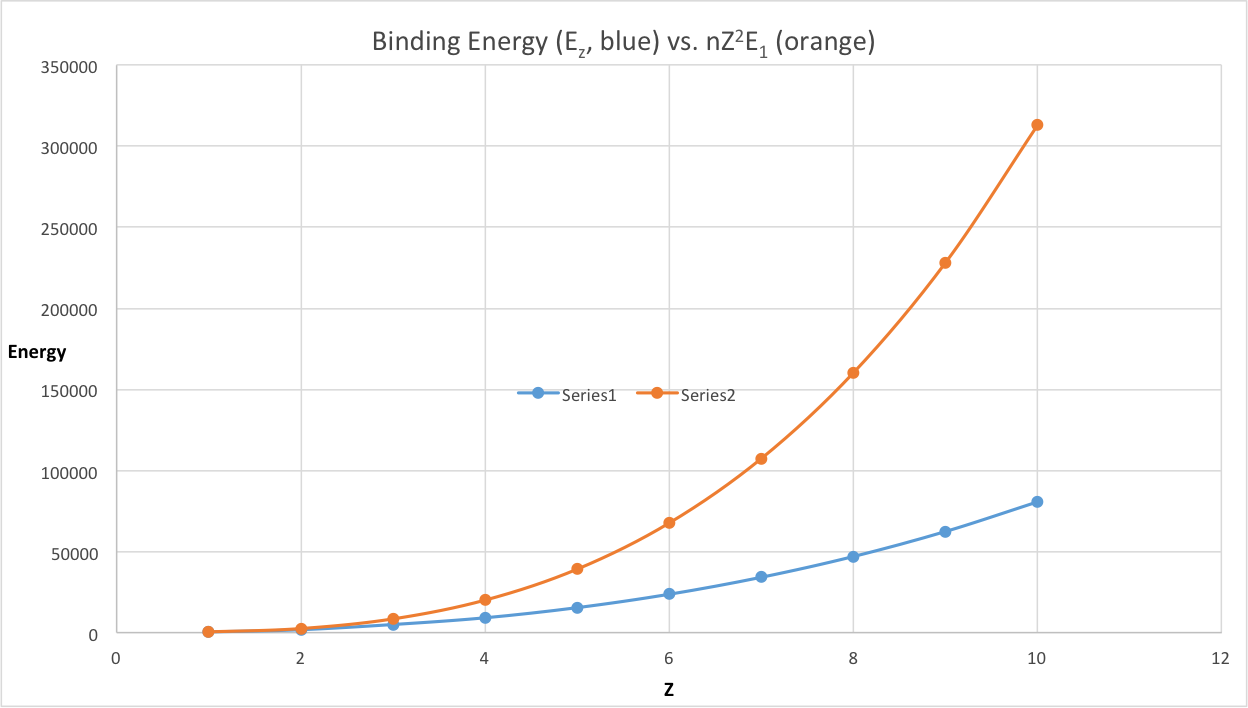
- Plot up this binding energy \(E_Z\) vs. \(n\) on your favorite software (e.g., excel or matlab)
- Plot up the \(nZ^2E_1\) vs. \(n\) on same plot
- From these data, answer these questions:
- What is the definition of binding energy (i.e., total electronic energy) of these atoms?
- Why do the calculations give negative energies?
- What is the meaning of \(nZ^2E_{1}\) expression?
- What is the origin of the \(n\) in this expression?
- What is the origin of the \(Z^2\) in this expression?
- What is the origin of the \(E_{1}\) in this expression?
- What is the origin of difference between \(nZ^2E_1\)and \(E_Z\)?
- We can make an effective nuclear charge \(Z_{eff}\) that can be added to this expression such that this equation holds\[E_z = n Z_{eff}^2 E_{Z=1} \].Calculate the \(Z_{eff}\) for each of the ten atoms and plot up \(Z_{eff}\) vs. \(Z\). Explain the origin of this difference (use may want to reference Slater's Rules).
Ans:
1. Definition of binding energy \(E_{tot}\):
Binding energy \(E_{tot}\) is the total electronic energy for the system and it does not include nuclear energies (e.g., vibration and rotational). The "chemical" reaction associated with this energy for the \(M\) atom with \(n\) electrons is
\[ M \rightarrow ne^- + M^{n+} \]
The expression for Binding Energy would be calculated from the energies E of each species:
\[ E_{tot} = nE(e^-) + E(M^{n+}) - E(M) \]
\(nE \big( e^{-} \big) + E\big(M^{n+}\big)\) are the energies of the products;
\(E\big(M\big)\) is the energy of the reactant.
Since kinetic energy of any species is not included in this discussion, only the energy of the \(M\) species needs to be explicitly calculated.
2. Why do the calculations give negative energies:
Because it is calculating the \(E(M)\), which is the electronic energy for the \(M\) species, and it is usually negative. Take the example of hydrogen atom, the electronic energy of hydrogen is always negative, because the zero potential energy was chosen as the potential of the system when the electron is infinitely far away from the nucleus, i.e., when it is fully ionized. \( E(M^{n+}) \) is zero according to the calculations.
3. What is the meaning of \(nZ^2E_{1}\) expression?
Ans: This is the total electronic energy you obtain when you treat a multi-electron problem as multiple one-electron problems. That is, you treat each electron independently, assuming each of them is attracted by the nuclear charge (Ze), then each electron has the energy of \(E_{one electron}=-Z^2\dfrac{R}{n^2} = - Z^2 R\) with n=1. Remember for one electron problems, the electronic energy is given as \(E_n=-Z^2\dfrac{R}{n^2}\), so \(E_1=-R\) and (E_{one electron}=-Z^2\dfrac{R}{n^2} = - Z^2 E_1\). Therefore, n electrons will have the total energy of \(E_Z=nE_{one electron}=nZ^2E_{1}\).
4. What is the origin of the difference between \(nZ^2E_1\) and E_Z?
Ans: The difference originates from the value of Z. When you have multiple electrons, they will shield each other, and therefore the effective nuclear charges that they feel will not be Z.
5. Effective nulcear charges
Using the following formulae to calculate effective nulcear charges:
\[Z_{eff}=\sqrt{\dfrac{E_z}{nE_1}}\]
The calculated values for effective nuclear charges are listed on the rightmost column of the table above. They are close to the effective nuclear charges experienced by the valence electrons calculated by Slater's rules.
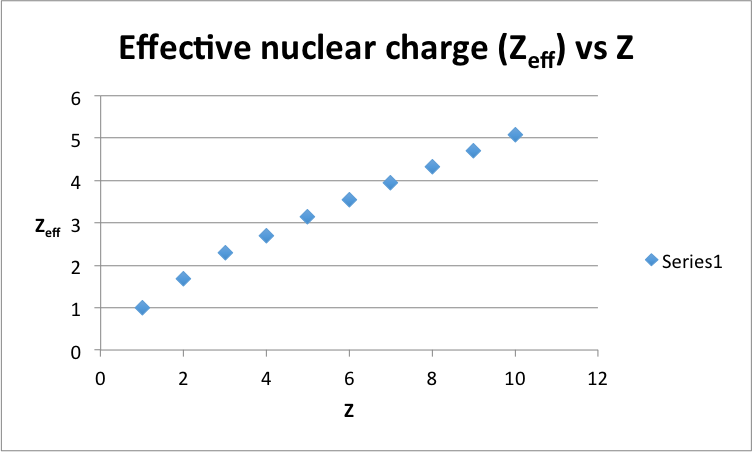
Note that Z=n, in these plots. (n is the number of electrons, and Z is the nuclear charge.)
