Homework 7A Key

Q1

Show that the hydrogenic wavefunctions \( \psi_{1s} \) and \( \psi_{2s} \) are mutually orthogonal and normalized.

To show that \( \psi_{1s} \) and \( \psi_{2s} \) are mutually orthogonal and normalized we need to verify three integrals:

\[ \langle \psi_{1s}| \psi_{2s} \rangle =0 \]

\[ \langle \psi_{1s}| \psi_{1s} \rangle =1\]

\[ \langle \psi_{2s}| \psi_{2s} \rangle =1\]

The solutions to the hydrogen atom Schrödinger equation are functions that are products of a spherical harmonic functions and a radial function.

\[ \psi _{n, l, m_l } (r, \theta , \phi) = R_{n,l} (r) Y^{m_l}_l (\theta , \phi) \]

Relevant radial functions and spherical harmonics we get from the tables:

\[ \psi_{1s}=\psi_{100} (r, \theta , \phi) =R_{1,0} (r) Y^{0}_0 (\theta , \phi) = 2 \left (\dfrac {Z}{a_0} \right ) ^{3/2} e^{-\frac {Zr}{a_0}} \times \dfrac {1}{\sqrt {4 \pi}}\]

\[ \psi_{2s}=\psi_{200} (r, \theta , \phi) =R_{2,0} (r) Y^{0}_0 (\theta , \phi) = \dfrac {1}{2 \sqrt {2}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} (2 - \frac {Zr}{a_0}) e^{-\frac {Zr}{2a_0}} \times \dfrac {1}{\sqrt {4 \pi}}\]

where \(Z\) is the atomic number of the nucleus, \(a_0\) is the Bohr radius and r is the radial variable.

Both radial functions and spherical harmonics are normalized separately, therefore, we will use \(r^2 \sin \theta \) (NO \(4\pi\) factor!) as Jacobian for calculating integral over spherical coordinates.

For calculation use one of the Gaussian integrals \(\int_{0}^{\infty} x^n e^{-ax} = \dfrac{n!}{a^{n+1}}\)

\[ \langle \psi_{1s}| \psi_{1s} \rangle = \langle \psi_{100} (r, \theta , \phi) | \psi_{100} (r, \theta , \phi) \rangle = \langle R_{1,0} (r) Y^{0}_0 (\theta , \phi) | R_{1,0} (r) Y^{0}_0 (\theta , \phi) \rangle = \langle Y^{0}_0 (\theta , \phi) | Y^{0}_0 (\theta , \phi) \rangle \langle R_{1,0} (r) | R_{1,0} (r) \rangle = \\ \int_{0}^{\pi} \int_{0}^{ 2 \pi} (\dfrac {1}{\sqrt{4 \pi}})^2 \sin \theta d \phi d \theta \int_{0}^{\infty} (2 \left (\dfrac {Z}{a_0} \right ) ^{3/2} e^{-\frac {Zr}{a_0}} )^2 r^2 dr= \int_{0}^{\pi} \int_{0}^{ 2 \pi} (\dfrac {1}{\sqrt{4 \pi}})^2 \sin \theta d \phi d \theta \int_{0}^{\infty} 4 \left (\dfrac {Z}{a_0} \right) ^{3} e^{-\frac {2Zr}{a_0}} r^2 dr = \int_{0}^{\pi} \int_{0}^{ 2 \pi} \dfrac {1}{4 \pi} \sin \theta d \phi d \theta \int_{0}^{\infty} 4 \left (\dfrac {Z}{a_0} \right) e^{-\frac {2Zr}{a_0}} \left (\dfrac {Zr}{a_0} \right) ^{2} dr = - \dfrac {1} {4 \pi} \cos \theta \Biggr\rvert_{0}^{\pi} \phi \Biggr\rvert_{0}^{2\pi} 4\dfrac{2!}{2^{2+1}} = \\ - \dfrac {1} {4 \pi} (\cos(\pi) - \cos(0)) (2\pi - 0) 4\dfrac{2}{2^3} = - \dfrac {1} {4 \pi} (-1 - 1) 2\pi \times 1 = 1 \]

\[ \langle \psi_{2s}| \psi_{2s} \rangle = \langle \psi_{200} (r, \theta , \phi) | \psi_{200} (r, \theta , \phi) \rangle = \langle R_{2,0} (r) Y^{0}_0 (\theta , \phi) | R_{2,0} (r) Y^{0}_0 (\theta , \phi) \rangle = \langle Y^{0}_0 (\theta , \phi) | Y^{0}_0 (\theta , \phi) \rangle \langle R_{2,0} (r) | R_{2,0} (r) \rangle = \\ 1 \times \langle R_{2,0} (r) | R_{2,0} (r) \rangle ={shown \ above}= \int_{0}^{\infty} r^2 R_{2,0}^*(r) R_{2,0}(r) dr = \int_{0}^{\infty} r^2 (\dfrac {1}{2 \sqrt {2}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} (2 - \frac {Zr}{a_0}) e^{-\frac {Zr}{2a_0}} )^2 dr= \\ \int_{0}^{\infty} r^2 \dfrac {1}{8}\left (\dfrac {Z}{a_0} \right ) ^{3} (2 - \frac {Zr}{a_0})^2 e^{-\frac {Zr}{a_0}} dr= \int_{0}^{\infty} r^2 \dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{3} (4 - 4 \frac {Zr}{a_0} +(\frac {Zr}{a_0})^2) e^{-\frac {Zr}{a_0}} dr = \\ \int_{0}^{\infty} 4 r^2 \dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{3} e^{-\frac {Zr}{a_0}} dr - \int_{0}^{\infty} 4 \frac {Zr}{a_0} r^2 \dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{3} e^{-\frac {Zr}{a_0}} dr +\int_{0}^{\infty} (\frac {Zr}{a_0})^2 r^2 \dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{3} e^{-\frac {Zr}{a_0}} dr= \\ \int_{0}^{\infty} r^2 \dfrac {1}{2} \left (\dfrac {Z}{a_0} \right ) ^{3} e^{-\frac {Zr}{a_0}} dr - \int_{0}^{\infty} \frac {Zr}{a_0} r^2 \dfrac {1}{2} \left (\dfrac {Z}{a_0} \right ) ^{3} e^{-\frac {Zr}{a_0}} dr + \int_{0}^{\infty} (\frac {Zr}{a_0})^2 r^2 \dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{3} e^{-\frac {Zr}{a_0}} dr = \\ \int_{0}^{\infty} \dfrac {1}{2} \left (\dfrac {Z}{a_0} \right ) ^{3} r^2 e^{-\frac {Zr}{a_0}} dr - \int_{0}^{\infty} \dfrac {1}{2} \left (\dfrac {Z}{a_0} \right ) ^{4} r^3 e^{-\frac {Zr}{a_0}} dr+ \int_{0}^{\infty} \dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{5} r^4 e^{-\frac {Zr}{a_0}} dr = \dfrac {a_0}{Z} (\dfrac {1}{2} \dfrac {Z}{a_0} \dfrac{2!}{1^{2+1}} - \dfrac {1}{2} \dfrac {Z}{a_0} \dfrac{3!}{1^{3+1}} +\dfrac {1}{8} \dfrac {Z}{a_0} \dfrac{4!}{1^{4+1}} )= \dfrac {a_0}{Z}( \dfrac {1}{2} \dfrac {Z}{a_0} 2 - \dfrac {1}{2} \dfrac {Z}{a_0} \times 1 \times 2 \times 3 +\dfrac {1}{8} \dfrac {Z}{a_0} \times 1 \times 2 \times 3 \times 4) = 1 - 3 +3 =1\]

\[ \langle \psi_{1s}| \psi_{2s} \rangle = \langle \psi_{100} (r, \theta , \phi) | \psi_{200} (r, \theta , \phi) \rangle = \langle R_{1,0} (r) Y^{0}_0 (\theta , \phi) | R_{2,0} (r) Y^{0}_0 (\theta , \phi) \rangle = \langle Y^{0}_0 (\theta , \phi) | Y^{0}_0 (\theta , \phi) \rangle \langle R_{1,0} (r) | R_{2,0} (r) \rangle = \\ 1 \times \langle R_{1,0} (r) | R_{2,0} (r) \rangle ={shown \ above}= \int_{0}^{\infty} r^2 R_{1,0}^*(r) R_{2,0}(r) dr= \int_{0}^{\infty} r^2 2 \left (\dfrac {Z}{a_0} \right ) ^{3/2} e^{-\frac {Zr}{a_0}} \dfrac {1}{2 \sqrt {2}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} (2 - \frac {Zr}{a_0}) e^{-\frac {Zr}{2a_0}} dr= \\ \dfrac {1}{\sqrt {2}} \int_{0}^{\infty} \left (\dfrac {Z}{a_0} \right ) ^{3} (2 - \frac {Zr}{a_0}) e^{-\frac {3Zr}{2a_0}} r^2 dr = \dfrac {1}{\sqrt {2}} \int_{0}^{\infty} \left (\dfrac {Z}{a_0} \right ) ^{3} 2 e^{-\frac {3Zr}{2a_0}} r^2 dr - \dfrac {1}{\sqrt {2}} \int_{0}^{\infty} \left (\dfrac {Z}{a_0} \right ) ^{3} \frac {Zr}{a_0} e^{-\frac {3Zr}{2a_0}} r^2 dr = \\ \dfrac {1}{\sqrt {2}} 2 \int_{0}^{\infty} \dfrac {Z}{a_0} e^{-\frac {3Zr}{2a_0}} \left (\dfrac {Zr}{a_0} \right ) ^{2} dr - \dfrac {1}{\sqrt {2}} \int_{0}^{\infty} \dfrac {Z}{a_0} e^{-\frac {3Zr}{2a_0}} \left (\dfrac {Zr}{a_0} \right ) ^{3} dr = \\ \dfrac {2}{\sqrt {2}} \int_{0}^{\infty} \dfrac {Z}{a_0} e^{-\frac {3Zr}{2a_0}} \left (\dfrac {Zr}{a_0} \right ) ^{2} dr - \dfrac {1}{\sqrt {2}} \int_{0}^{\infty} \dfrac {Z}{a_0} e^{-\frac {3Zr}{2a_0}} \left (\dfrac {Zr}{a_0} \right ) ^{3} dr = \dfrac {2}{\sqrt {2}} \dfrac {Z}{a_0} \int_{0}^{\infty} e^{-\frac {3Zr}{2a_0}} \left (\dfrac {Zr}{a_0} \right ) ^{2} dr - \dfrac {1}{\sqrt {2}} \dfrac {Z}{a_0} \int_{0}^{\infty} e^{-\frac {3Zr}{2a_0}} \left (\dfrac {Zr}{a_0} \right ) ^{3} dr= \dfrac {a_0}{Z} (\dfrac {2}{\sqrt {2}} \dfrac {Z}{a_0} \dfrac{2!}{(\dfrac{3}{2})^{2+1}} - \dfrac {1}{\sqrt {2}} \dfrac {Z}{a_0} \dfrac{3!}{(\dfrac{3}{2})^{3+1}} ) = \\ \dfrac {a_0}{Z}(\dfrac {2}{\sqrt {2}} \dfrac {Z}{a_0} \dfrac{1 \times 2 \times 2^3}{3^3} - \dfrac {1}{\sqrt {2}} \dfrac {Z}{a_0} \dfrac{1 \times 2 \times 3 \times 2^4}{3^4}) = \dfrac {a_0}{Z} (\dfrac {2}{\sqrt {2}} \dfrac {Z}{a_0} \dfrac{16}{27} - \dfrac {1}{\sqrt {2}} \dfrac {Z}{a_0} \dfrac{96}{81}) = \dfrac {a_0}{Z} (\dfrac {1}{\sqrt {2}} \dfrac {Z}{a_0} \dfrac{32}{27} - \dfrac {1}{\sqrt {2}} \dfrac {Z}{a_0} \dfrac{96}{81}) =0 \]

Q2

The most probable radius for an electron in the 1s wavefunction is called the Bohr radius (\(a_o\)) and is 52.9 pm. What is the most probable radius for an electron in the 2s wavefunction?

The most probable radius for 2s will be found by finding the maximum of the radial probability density.

\[r^2 R_{2,0}^*(r) R_{2,0}(r)\]

\[ R_{2,0} (r) = \dfrac {1}{2 \sqrt {2}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} (2 - \frac {Zr}{a_0}) e^{-\frac {Zr}{2a_0}} \]

where \(Z\) is the atomic number of the nucleus, \(a_0\) is the Bohr radius and r is the radial variable.

\[r^2 R_{2,0}^*(r) R_{2,0}(r) = r^2 (\dfrac {1}{2 \sqrt {2}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} (2 - \frac {Zr}{a_0}) e^{-\frac {Zr}{2a_0}} )^2 = r^2 \dfrac {1}{8}\left (\dfrac {Z}{a_0} \right ) ^{3} (2 - \frac {Zr}{a_0})^2 e^{-\frac {Zr}{a_0}}= r^2 \dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{3} (4 - 4 \frac {Zr}{a_0} +(\frac {Zr}{a_0})^2) e^{-\frac {Zr}{a_0}} = \\ 4 r^2 \dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{3} e^{-\frac {Zr}{a_0}} - 4 \frac {Zr}{a_0} r^2 \dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{3} e^{-\frac {Zr}{a_0}} + (\frac {Zr}{a_0})^2 r^2 \dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{3} e^{-\frac {Zr}{a_0}} = r^2 \dfrac {1}{2} \left (\dfrac {Z}{a_0} \right ) ^{3} e^{-\frac {Zr}{a_0}} - \frac {Zr}{a_0} r^2 \dfrac {1}{2} \left (\dfrac {Z}{a_0} \right ) ^{3} e^{-\frac {Zr}{a_0}} + (\frac {Zr}{a_0})^2 r^2 \dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{3} e^{-\frac {Zr}{a_0}} = \\ \dfrac {1}{2} \left (\dfrac {Z}{a_0} \right ) ^{3} r^2 e^{-\frac {Zr}{a_0}} - \dfrac {1}{2} \left (\dfrac {Z}{a_0} \right ) ^{4} r^3 e^{-\frac {Zr}{a_0}} + \dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{5} r^4 e^{-\frac {Zr}{a_0}}\]

\[\dfrac{d}{dr} (r^2 R_{2,0}^*(r) R_{2,0}(r)) = \dfrac{d}{dr} ( \dfrac {1}{2} \left (\dfrac {Z}{a_0} \right ) ^{3} r^2 e^{-\frac {Zr}{a_0}} - \dfrac {1}{2} \left (\dfrac {Z}{a_0} \right ) ^{4} r^3 e^{-\frac {Zr}{a_0}} + \dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{5} r^4 e^{-\frac {Zr}{a_0}} ) = \dfrac {1}{2} \left (\dfrac {Z}{a_0} \right ) ^{3} 2r e^{-\frac {Zr}{a_0}} + \dfrac {1}{2} \left (\dfrac {Z}{a_0} \right ) ^{3} r^2 (-\frac {Z}{a_0})e^{-\frac {Zr}{a_0}} - \dfrac {1}{2} \left (\dfrac {Z}{a_0} \right ) ^{4} 3r^2 e^{-\frac {Zr}{a_0}} - \dfrac {1}{2} \left (\dfrac {Z}{a_0} \right ) ^{4} r^3 (-\frac {Z}{a_0}) e^{-\frac {Zr}{a_0}} + \dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{5} 4r^3 e^{-\frac {Zr}{a_0}} + \dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{5} r^4 (-\frac {Z}{a_0}) e^{-\frac {Zr}{a_0}} = \\ \left (\dfrac {Z}{a_0} \right ) ^{3} e^{-\frac {Zr}{a_0}} ( \dfrac {1}{2} 2r- \dfrac {1}{2} r^2 \frac {Z}{a_0} - \dfrac {1}{2} \dfrac {Z}{a_0} 3r^2 + \dfrac {1}{2} \dfrac {Z}{a_0} r^3 \frac {Z}{a_0} + \dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{2} 4r^3 - \dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{2} r^4 \frac {Z}{a_0} ) = \\ \left (\dfrac {Z}{a_0} \right ) ^{3} e^{-\frac {Zr}{a_0}} ( \dfrac {1}{2} 2r- \dfrac {1}{2} \frac {Z}{a_0} r^2- \dfrac {1}{2} \dfrac {Z}{a_0} 3r^2 + \dfrac {1}{2} \left (\dfrac {Z}{a_0} \right ) ^{2} r^3 + \dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{2} 4r^3 - \dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{3} r^4 ) = \\ \left (\dfrac {Z}{a_0} \right ) ^{3} r e^{-\frac {Zr}{a_0}} (1 -2\frac {Z}{a_0}r + \left (\dfrac {Z}{a_0} \right ) ^{2} r^2 -\dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{3} r^3 )=0\]

Although, \(r=0\) is a solution to the equation above, it corresponds to the least probable radius as electron cannot be found on top of nucleus. Therefore, search for the most probable radius among the solutions of the following equation:

\[ 1 -2\frac {Z}{a_0}r + \left (\dfrac {Z}{a_0} \right ) ^{2} r^2 -\dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{3} r^3 =0 \]

\[ 8- 16\frac {Z}{a_0}r + 8 \left (\dfrac {Z}{a_0} \right ) ^{2} r^2 - \left (\dfrac {Z}{a_0} \right ) ^{3} r^3 =0 \]

There are three roots for this equation: \(r=\dfrac {2a_0}{Z} \ and \ \dfrac {a_0}{Z} (3 \pm \sqrt{5}) \). These are extrema of the radial distribution (both maxima and minima). Mathematically you can differentiate between maxima and minima by taking the second derivative. It would be positive for minima and negative for maxima. However, here taking derivative is not mandatory. We could assign maxima and minima by remembering the shape of the curve for radial distribution for 2s orbital and by comparing the roots. The roots compare as \(\dfrac {a_0}{Z} (3 - \sqrt{5}) = 0.76 \dfrac {a_0}{Z} < \dfrac {2a_0}{Z} < \dfrac {a_0}{Z} (3 + \sqrt{5}) = 5.2 \dfrac {a_0}{Z}\). Therefore, assignment is as follows:

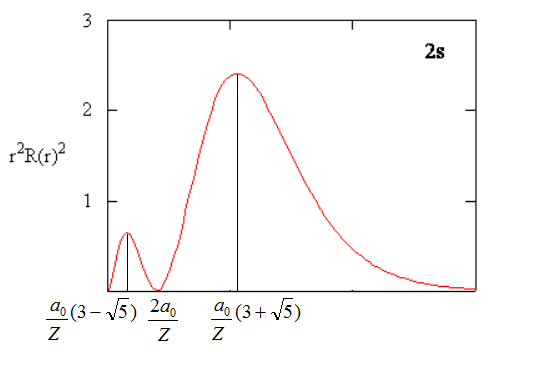
Global maximum is at \( r= \dfrac {a_0}{Z} (3+\sqrt{5}) = 5.2 \dfrac {a_0}{Z} \).

Q3

Determine the probability of finding an electron between each of the following radii for each given orbital. Using your favorite plotting tool or program, plot the probability as a function of radius. Identify each requested region.

Orbital	0 - \(a_o\)	0 - 168 pm	168 - 508 pm	508 - 1,000,000,000 pm
1s
2s
3s

Q4

Calculate the average radial expectation value \( \langle r \rangle \) for the maximum probability of electron density for the following hydrogenic orbitals (as a function of Z).

1. \(2s\)
2. \(2p_o\)
3. \(2p_{\pm 1}\)
4. \(3s\)
5. \(3d_o\)
6. \(3d_{\pm 1}\)

Hint: This requires volume integration! Do not forget the \(4\pi r^2 \) spherical volume element.

We need just \(r^2\) for Jacobian (or volume element) here, since we use radial functions and spherical harmonics that are normalized separately.

a. \[ \langle \psi_{200} (r, \theta , \phi) | r |\psi_{200} (r, \theta , \phi) \rangle = \langle \psi_{200} (r, \theta , \phi) | r |\psi_{200} (r, \theta , \phi) \rangle = \langle R_{2,0} (r) Y^{0}_0 (\theta , \phi) | r| R_{2,0} (r) Y^{0}_0 (\theta , \phi) \rangle = \langle Y^{0}_0 (\theta , \phi) | Y^{0}_0 (\theta , \phi) \rangle \langle R_{2,0} (r) | r | R_{2,0} (r) \rangle = \\ 1 \times \langle R_{2,0} (r) | r | R_{2,0} (r) \rangle = \int_{0}^{\infty} (\dfrac {1}{2 \sqrt {2}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} (2 - \frac {Zr}{a_0}) e^{-\frac {Zr}{2a_0}} )^2 r^3 dr = \int_{0}^{\infty} \dfrac {1}{2} \left (\dfrac {Z}{a_0} \right ) ^{3} r^3 e^{-\frac {Zr}{a_0}} dr - \int_{0}^{\infty} \dfrac {1}{2} \left (\dfrac {Z}{a_0} \right ) ^{4} r^4 e^{-\frac {Zr}{a_0}} dr+ \int_{0}^{\infty} \dfrac {1}{8} \left (\dfrac {Z}{a_0} \right ) ^{5} r^5 e^{-\frac {Zr}{a_0}} dr = \\ \dfrac{a_0}{Z} (\dfrac {1}{2}\dfrac{3!}{1^{3+1}} - \dfrac {1}{2} \dfrac{4!}{1^{4+1}} +\dfrac {1}{8} \dfrac{5!}{1^{5+1}})= \dfrac{a_0}{Z}(3-12+ 15) =\dfrac{6a_0}{Z}\]

b. \[ \langle \psi_{210} (r, \theta , \phi) | r |\psi_{210} (r, \theta , \phi) \rangle = \langle \psi_{210} (r, \theta , \phi) | r |\psi_{210} (r, \theta , \phi) \rangle = \langle R_{2,1} (r) Y^{0}_1 (\theta , \phi) | r| R_{2,1} (r) Y^{0}_1 (\theta , \phi) \rangle = \langle Y^{0}_1 (\theta , \phi) | Y^{0}_1 (\theta , \phi) \rangle \langle R_{2,1} (r) | r | R_{2,1} (r) \rangle = \\ 1 \times \langle R_{2,1} (r) | r | R_{2,1} (r) \rangle = \int_{0}^{\infty} (\dfrac {1}{2 \sqrt {6}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} \dfrac {Zr}{a_0} e^{-\dfrac {Zr}{2a_0}} )^2 r^3 dr = \dfrac {1}{4 \times 6} \int_{0}^{\infty} \left (\dfrac {Z}{a_0} \right ) ^{3} \left (\dfrac {Zr}{a_0} \right )^{2} e^{-\dfrac {Zr}{a_0}} r^3 dr = \dfrac {1}{4 \times 6} \int_{0}^{\infty} e^{-\dfrac {Zr}{a_0}} \left (\dfrac {Zr}{a_0} \right )^{5} dr = \dfrac {1}{4 \times 6} \dfrac {a_0}{Z} \dfrac{5!}{1^{5+1}} = \dfrac {120}{4 \times 6} \dfrac {a_0}{Z} =\dfrac {5a_0}{Z} \]

c. \[ \langle \psi_{21 \pm 1} (r, \theta , \phi) | r |\psi_{21\pm 1} (r, \theta , \phi) \rangle = \langle \psi_{21 \pm 1} (r, \theta , \phi) | r |\psi_{21 \pm 1} (r, \theta , \phi) \rangle = \langle R_{2,1} (r) Y^{\pm 1}_1 (\theta , \phi) | r| R_{2,1} (r) Y^{\pm 1}_1 (\theta , \phi) \rangle = \langle Y^{\pm 1}_1 (\theta , \phi) | Y^{\pm 1}_1 (\theta , \phi) \rangle \langle R_{2,1} (r) | r | R_{2,1} (r) \rangle = \\ 1 \times \langle R_{2,1} (r) | r | R_{2,1} (r) \rangle = \int_{0}^{\infty} (\dfrac {1}{2 \sqrt {6}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} \dfrac {Zr}{a_0} e^{-\dfrac {Zr}{2a_0}} )^2 r^3 dr = \dfrac {1}{4 \times 6} \int_{0}^{\infty} \left (\dfrac {Z}{a_0} \right ) ^{3} \left (\dfrac {Zr}{a_0} \right )^{2} e^{-\dfrac {Zr}{a_0}} r^3 dr = \dfrac {1}{4 \times 6} \int_{0}^{\infty} e^{-\dfrac {Zr}{a_0}} \left (\dfrac {Zr}{a_0} \right )^{5} dr = \dfrac {1}{4 \times 6} \dfrac {a_0}{Z} \dfrac{5!}{1^{5+1}} = \dfrac {120}{4 \times 6} \dfrac {a_0}{Z} =\dfrac {5a_0}{Z} \]

d. \[ \langle \psi_{300} (r, \theta , \phi) | r |\psi_{300} (r, \theta , \phi) \rangle = \langle \psi_{300} (r, \theta , \phi) | r |\psi_{300} (r, \theta , \phi) \rangle = \langle R_{3,0} (r) Y^{0}_0 (\theta , \phi) | r| R_{3,0} (r) Y^{0}_0 (\theta , \phi) \rangle = \langle Y^{0}_0 (\theta , \phi) | Y^{0}_0 (\theta , \phi) \rangle \langle R_{3,0} (r) | r | R_{3,0} (r) \rangle = \\ 1 \times \langle R_{3,0} (r) | r | R_{3,0} (r) \rangle = \int_{0}^{\infty} (\dfrac {1}{81 \sqrt {3}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} (27 - 18 \dfrac {Zr}{a_0} + 2(\dfrac {Zr}{a_0})^2) e^{-\dfrac {Zr}{3a_0}})^2 r^3 dr = \int_{0}^{\infty} \dfrac {1}{81^2 \times 3}\left (\dfrac {Z}{a_0} \right ) ^{3} (27 - 18 \dfrac {Zr}{a_0} + 2(\dfrac {Zr}{a_0})^2)^2 e^{-\dfrac {2Zr}{3a_0}} r^3 dr = \int_{0}^{\infty} \dfrac {1}{81^2 \times 3}\left (\dfrac {Z}{a_0} \right ) ^{3} (27^2 + 18^2 (\dfrac {Zr}{a_0})^2 + 2^2(\dfrac {Zr}{a_0})^4 - 2 \times 27 \times 18 \dfrac {Zr}{a_0} + 2 \times 27 \times 2(\dfrac {Zr}{a_0})^2 - 2 \times 18 \dfrac {Zr}{a_0} 2(\dfrac {Zr}{a_0})^2 ) e^{-\dfrac {2Zr}{3a_0}} r^3 dr = \int_{0}^{\infty} \dfrac {1}{81^2 \times 3}\left (\dfrac {Z}{a_0} \right ) ^{3} 27^2 e^{-\dfrac {2Zr}{3a_0}} r^3 dr + \int_{0}^{\infty} \dfrac {1}{81^2 \times 3}\left (\dfrac {Z}{a_0} \right ) ^{3} 18^2 (\dfrac {Zr}{a_0})^2 e^{-\dfrac {2Zr}{3a_0}} r^3 dr + \int_{0}^{\infty} \dfrac {1}{81^2 \times 3}\left (\dfrac {Z}{a_0} \right ) ^{3} 2^2(\dfrac {Zr}{a_0})^4 e^{-\dfrac {2Zr}{3a_0}} r^3 dr + \int_{0}^{\infty} \dfrac {1}{81^2 \times 3}\left (\dfrac {Z}{a_0} \right ) ^{3} (- 2 \times 27 \times 18 \dfrac {Zr}{a_0}) e^{-\dfrac {2Zr}{3a_0}} r^3 dr + \int_{0}^{\infty} \dfrac {1}{81^2 \times 3}\left (\dfrac {Z}{a_0} \right ) ^{3} 2 \times 27 \times 2(\dfrac {Zr}{a_0})^2 e^{-\dfrac {2Zr}{3a_0}} r^3 dr +\int_{0}^{\infty} \dfrac {1}{81^2 \times 3}\left (\dfrac {Z}{a_0} \right ) ^{3} (- 2 \times 18 \dfrac {Zr}{a_0} 2(\dfrac {Zr}{a_0})^2 ) e^{-\dfrac {2Zr}{3a_0}} r^3 dr = \int_{0}^{\infty} \dfrac {27^2}{81^2 \times 3}\left (\dfrac {Z}{a_0} \right ) ^{3} e^{-\dfrac {2Zr}{3a_0}} r^3 dr + \int_{0}^{\infty} \dfrac {18^2 }{81^2 \times 3}\left (\dfrac {Z}{a_0} \right ) ^{3} (\dfrac {Zr}{a_0})^2 e^{-\dfrac {2Zr}{3a_0}} r^3 dr + \int_{0}^{\infty} \dfrac {2^2}{81^2 \times 3}\left (\dfrac {Z}{a_0} \right ) ^{3} (\dfrac {Zr}{a_0})^4 e^{-\dfrac {2Zr}{3a_0}} r^3 dr - \int_{0}^{\infty} \dfrac {2 \times 27 \times 18}{81^2 \times 3}\left (\dfrac {Z}{a_0} \right )^{3} (\dfrac {Zr}{a_0}) e^{-\dfrac {2Zr}{3a_0}} r^3 dr + \int_{0}^{\infty} \dfrac {2 \times 27 \times 2}{81^2 \times 3}\left (\dfrac {Z}{a_0} \right ) ^{3} (\dfrac {Zr}{a_0})^2 e^{-\dfrac {2Zr}{3a_0}} r^3 dr - \int_{0}^{\infty} \dfrac {2 \times 18}{81^2 \times 3}\left (\dfrac {Z}{a_0} \right ) ^{3} \dfrac {Zr}{a_0} 2(\dfrac {Zr}{a_0})^2 e^{-\dfrac {2Zr}{3a_0}} r^3 dr = \dfrac {27^2}{81^2 \times 3} \int_{0}^{\infty} \left (\dfrac {Zr}{a_0} \right ) ^{3} e^{-\dfrac {2Zr}{3a_0}} dr + \dfrac {18^2 }{81^2 \times 3}\int_{0}^{\infty} \left (\dfrac {Zr}{a_0} \right ) ^{5} e^{-\dfrac {2Zr}{3a_0}} dr + \dfrac {2^2}{81^2 \times 3} \int_{0}^{\infty} \left (\dfrac {Zr}{a_0} \right ) ^{7} e^{-\dfrac {2Zr}{3a_0}} dr - \dfrac {2 \times 27 \times 18}{81^2 \times 3} \int_{0}^{\infty}\left (\dfrac {Zr}{a_0} \right )^{4} e^{-\dfrac {2Zr}{3a_0}} dr + \dfrac {2 \times 27 \times 2}{81^2 \times 3} \int_{0}^{\infty} \left (\dfrac {Zr}{a_0} \right ) ^{5} e^{-\dfrac {2Zr}{3a_0}} dr - \dfrac {2 \times 18 \times 2}{81^2 \times 3} \int_{0}^{\infty} \left (\dfrac {Zr}{a_0} \right ) ^{6} e^{-\dfrac {2Zr}{3a_0}} dr \]

e. \[ \langle \psi_{320} (r, \theta , \phi) | r |\psi_{320} (r, \theta , \phi) \rangle = \langle \psi_{320} (r, \theta , \phi) | r |\psi_{320} (r, \theta , \phi) \rangle = \langle R_{3,2} (r) Y^{0}_2 (\theta , \phi) | r| R_{3,2} (r) Y^{0}_2 (\theta , \phi) \rangle = \langle Y^{0}_2 (\theta , \phi) | Y^{0}_2 (\theta , \phi) \rangle \langle R_{3,2} (r) | r | R_{3,2} (r) \rangle = \\ 1 \times \langle R_{3,2} (r) | r | R_{3,2} (r) \rangle = \int_{0}^{\infty} ( \dfrac {1}{81 \sqrt {30}}\left (\dfrac {Z}{a_0} \right ) ^{3/2}( \dfrac {Zr}{a_0}) ^2 e^{-\dfrac {Zr}{3a_0}} )^2 r^3 dr = \dfrac {1}{81^2 \times 30} \int_{0}^{\infty} \left (\dfrac {Z}{a_0} \right ) ^{3} ( \dfrac {Zr}{a_0}) ^4 e^{-\dfrac {2Zr}{3a_0}} r^3 dr = \dfrac {1}{81^2 \times 30} \int_{0}^{\infty} \left (\dfrac {Zr}{a_0} \right ) ^{7} e^{-\dfrac {2Zr}{3a_0}} dr = \dfrac {1}{81^2 \times 30} \dfrac {a_0}{Z} \dfrac{7!}{(\frac{2}{3})^{7+1}} = \dfrac {1}{81^2 \times 30} \dfrac {a_0}{Z} \dfrac{5040 \times 3^8 }{2^{8}} = \dfrac {1}{6561 \times 30} \dfrac {a_0}{Z} \dfrac{5040 \times 6561 }{256} = \dfrac {5040}{256 \times 30} \dfrac {a_0}{Z} = \dfrac {168}{256}\dfrac {a_0}{Z}= \dfrac {42}{64} \dfrac {a_0}{Z}= \dfrac {21}{32} \dfrac {a_0}{Z} \]

f. \[ \langle \psi_{32 \pm 1} (r, \theta , \phi) | r |\psi_{32 \pm 1} (r, \theta , \phi) \rangle = \langle \psi_{32 \pm 1} (r, \theta , \phi) | r |\psi_{32 \pm 1} (r, \theta , \phi) \rangle = \langle R_{3,2} (r) Y^{ \pm 1}_2 (\theta , \phi) | r| R_{3,2} (r) Y^{ \pm 1}_2 (\theta , \phi) \rangle = \langle Y^{ \pm 1}_2 (\theta , \phi) | Y^{ \pm 1}_2 (\theta , \phi) \rangle \langle R_{3,2} (r) | r | R_{3,2} (r) \rangle = \\ 1 \times \langle R_{3,2} (r) | r | R_{3,2} (r) \rangle = \int_{0}^{\infty} ( \dfrac {1}{81 \sqrt {30}}\left (\dfrac {Z}{a_0} \right ) ^{3/2}( \dfrac {Zr}{a_0}) ^2 e^{-\dfrac {Zr}{3a_0}} )^2 r^3 dr = \ shown \ in \ point \ e. = \dfrac {21}{32} \dfrac {a_0}{Z} \]

Q5

Calculate the uncertainty of the radius of the electron in the 1s wavefunction (i.e., \( \Delta r \)).

\[ \Delta r = \sqrt{ \langle r^2 \rangle - \langle r \rangle^2}\]

Use \(r^2 \) (NO \(4\pi\) factor!) as Jacobian for calculating integral over radial distribution since radial functions and spherical coordinates are normalized separately.

\[ \langle r \rangle = \langle \psi_{1s}| r | \psi_{1s} \rangle = \langle \psi_{100} (r, \theta , \phi) |r | \psi_{100} (r, \theta , \phi) \rangle = \langle R_{1,0} (r) Y^{0}_0 (\theta , \phi) | r | R_{1,0} (r) Y^{0}_0 (\theta , \phi) \rangle = \langle Y^{0}_0 (\theta , \phi) | Y^{0}_0 (\theta , \phi) \rangle \langle R_{1,0} (r) |r | R_{1,0} (r) \rangle = 1 \times \langle R_{1,0} (r) |r | R_{1,0} (r) \rangle = \\ 1 \times \int_{0}^{\infty} (2 \left (\dfrac {Z}{a_0} \right ) ^{3/2} e^{-\frac {Zr}{a_0}} )^2 r^3 dr = \int_{0}^{\infty} 4 \left (\dfrac {Z}{a_0} \right) ^{3} e^{-\frac {2Zr}{a_0}} r^3 dr = 4 \int_{0}^{\infty} e^{-\frac {2Zr}{a_0}} \left(\dfrac {Zr}{a_0} \right) ^{3} dr=4 \dfrac {a_0}{Z}\dfrac{3!}{2^{3+1}} =4 \dfrac {a_0}{Z}\dfrac{6}{16} = \dfrac {3a_0}{2Z} \]

\[ \langle r^2 \rangle = \langle \psi_{1s}| r^2 | \psi_{1s} \rangle = \langle \psi_{100} (r, \theta , \phi) |r^2 | \psi_{100} (r, \theta , \phi) \rangle = \langle R_{1,0} (r) Y^{0}_0 (\theta , \phi) | r^2 | R_{1,0} (r) Y^{0}_0 (\theta , \phi) \rangle = \langle Y^{0}_0 (\theta , \phi) | Y^{0}_0 (\theta , \phi) \rangle \langle R_{1,0} (r) |r^2 | R_{1,0} (r) \rangle = 1 \times \langle R_{1,0} (r) |r^2| R_{1,0} (r) \rangle = \\ 1 \times \int_{0}^{\infty} (2 \left (\dfrac {Z}{a_0} \right ) ^{3/2} e^{-\frac {Zr}{a_0}} )^2 r^4 dr = \int_{0}^{\infty} 4 \left (\dfrac {Z}{a_0} \right)^{3} e^{-\frac {2Zr}{a_0}} r^4 dr = 4 \left(\dfrac {a_0}{Z} \right) \int_{0}^{\infty} e^{-\frac {2Zr}{a_0}} \left(\dfrac {Zr}{a_0} \right)^{4} dr = 4 \left(\dfrac {a_0}{Z} \right)^{2} \dfrac{4!}{2^{4+1}} = 4 \left(\dfrac {a_0}{Z} \right)^2 \dfrac{24}{32} = 4 \left(\dfrac {a_0}{Z} \right)^2 \dfrac{3}{4} = 3 \left(\dfrac {a_0}{Z} \right)^2 \]

\[ \Delta r = \sqrt{ \langle r^2 \rangle - \langle r \rangle^2} = \sqrt{3 \left(\dfrac {a_0}{Z} \right)^2- (\dfrac {3a_0}{2Z} )^2} = \sqrt{ 3 \left(\dfrac {a_0}{Z} \right)^2 - \left(\dfrac {3a_0}{2Z} \right)^2 } \] \[ = \sqrt{ 3 \left(\dfrac {a_0}{Z} \right)^2 - \dfrac {9}{4} \left(\dfrac {a_0}{Z} \right)^2} = \dfrac {a_0}{Z} \sqrt{ 3 - \dfrac {9}{4} }= \dfrac {a_0}{Z} \sqrt{ \dfrac {12}{4} - \dfrac {9}{4} }= \dfrac {a_0}{Z} \sqrt{ \dfrac {3}{4} }= \dfrac {\sqrt{3}}{2} \dfrac {a_0}{Z}\]

Q6

Evaluate the following commutators:

1. \( \left[ \hat{L_x}, \hat{L_y}\right] \)
2. \(\left[\hat{L_y}, \left[ \hat{L_x}, \hat{L_z}\right]\right] \)
3. \(\left[\hat{L_z}, \left[ \hat{L^2_z}, \hat{L_z}\right]\right] \)
4. \( \left[\hat{L_y}, \left[ \hat{L_x}^2, \hat{L_z}\right]\right] \)
5. \( \hat{L_z}\left[ \hat{L_x}, \hat{L_y}\right] \)
6. \( \hat{L^2}\left[ \hat{L_x}, \hat{L_y}\right] \)

a. \( \left[ \hat{L_x}, \hat{L_y}\right] = i \hbar \hat{L_z}\)

b. \(\left[\hat{L_y}, \left[ \hat{L_x}, \hat{L_z}\right]\right] = [\hat{L_y}, - i \hbar \hat{L_y} ] = -i \hbar [ \hat{L_y}, \hat{L_y}] = 0\)

c. \(\left[\hat{L_z}, \left[ \hat{L^2_z}, \hat{L_z}\right]\right] = [\hat{L_z}, [ \hat{L_z}\hat{L_z}, \hat{L_z}]] = [\hat{L_z}, (\hat{L_z}[ \hat{L_z}, \hat{L_z}] + [\hat{L_z}, \hat{L_z}] \hat{L_z}) ] =[\hat{L_z}, (0+0)]=0\)

d. \( \left[\hat{L_y}, \left[ \hat{L_x}^2, \hat{L_z}\right]\right] = [\hat{L_z}, [ \hat{L_x}\hat{L_x}, \hat{L_z}]] = [\hat{L_z}, (\hat{L_x}[ \hat{L_x}, \hat{L_z}] + [\hat{L_x}, \hat{L_z}] \hat{L_x}) ] = [\hat{L_z}, (\hat{L_x} (- i \hbar \hat{L_y})+ (- i \hbar \hat{L_y}) \hat{L_x}) ] = (- i \hbar) [\hat{L_z}, (\hat{L_x} \hat{L_y}+ \hat{L_y} \hat{L_x}) ] = (- i \hbar) ([\hat{L_z}, \hat{L_x} \hat{L_y}]+ [\hat{L_z},\hat{L_y} \hat{L_x} ] )= (- i \hbar) (\hat{L_x}[\hat{L_z},\hat{L_y}] + [\hat{L_z}, \hat{L_x}] \hat{L_y}+ \hat{L_y}[\hat{L_z},\hat{L_x}] + [\hat{L_z}, \hat{L_y}] \hat{L_x}) = (- i \hbar) (\hat{L_x}(- i \hbar \hat{L_x})+ i \hbar \hat{L_y}\hat{L_y}+ \hat{L_y} i \hbar \hat{L_y} +(- i \hbar \hat{L_x})\hat{L_x})= (- i \hbar) (- i \hbar \hat{L_x}^2 +i \hbar \hat{L_y}^2+i \hbar \hat{L_y}^2 - i \hbar \hat{L_x}^2) = - 2\hbar^2(\hat{L_x}^2-\hat{L_y}^2)\)

e.\( \hat{L_z}\left[ \hat{L_x}, \hat{L_y}\right] = [\hat{L_z}, i \hbar \hat{L_z} ] =i \hbar [\hat{L_z}, \hat{L_z} ] =0\)

f. \( \hat{L^2}\left[ \hat{L_x}, \hat{L_y}\right] = \hat{L^2} i \hbar \hat{L_z} = i \hbar \hat{L^2} \hat{L_z}\)

Q7

1. What is the average value of the kinetic energy for the \( \psi_{320} \) wavefunction?
2. What is the average value of the potential energy for the \( \psi_{320} \) wavefunction?
3. What is the relationship between the kinetic and potential energies in terms of magnitude (Hint: Virial Theorem)?

a. \[ \hat{KE} = \dfrac{-\hbar^2 \left[ \dfrac{\partial}{\partial r} \left( r^2 \dfrac{\partial}{\partial r} \right) + \dfrac{1}{\sin{\theta}}\dfrac{\partial}{\partial \theta} \left(\sin{\theta}\dfrac{\partial}{\partial \theta}\right)+\dfrac{1}{\sin^2{\theta}}\dfrac{\partial^2}{\partial\phi^2}\right]}{2\mu r^2} \]

\[ \langle \hat{KE} \rangle = \langle \psi_{320} (r, \theta , \phi) | \hat{KE} |\psi_{320} (r, \theta , \phi) \rangle = \langle \psi_{320} (r, \theta , \phi) | \dfrac{-\hbar^2 \left[ \dfrac{\partial}{\partial r} \left( r^2 \dfrac{\partial}{\partial r} \right) + \dfrac{1}{\sin{\theta}}\dfrac{\partial}{\partial \theta} \left(\sin{\theta}\dfrac{\partial}{\partial \theta}\right)+\dfrac{1}{\sin^2{\theta}}\dfrac{\partial^2}{\partial\phi^2}\right]}{2\mu r^2} |\psi_{320} (r, \theta , \phi) \rangle = \langle R_{3,2} (r) Y^{0}_2 (\theta , \phi) | \dfrac{-\hbar^2 \left[ \dfrac{\partial}{\partial r} \left( r^2 \dfrac{\partial}{\partial r} \right) + \dfrac{1}{\sin{\theta}}\dfrac{\partial}{\partial \theta} \left(\sin{\theta}\dfrac{\partial}{\partial \theta}\right)+\dfrac{1}{\sin^2{\theta}}\dfrac{\partial^2}{\partial\phi^2}\right]}{2\mu r^2} | R_{3,2} (r) Y^{0}_2 (\theta , \phi) \rangle = \langle Y^{0}_2 (\theta , \phi) | -\hbar^2 \left[ \dfrac{1}{\sin{\theta}}\dfrac{\partial}{\partial \theta} \left(\sin{\theta}\dfrac{\partial}{\partial \theta}\right)+\dfrac{1}{\sin^2{\theta}}\dfrac{\partial^2}{\partial\phi^2}\right] | Y^{0}_2 (\theta , \phi) \rangle \langle R_{3,2} (r) | \dfrac{ \dfrac{\partial}{\partial r} \left( r^2 \dfrac{\partial}{\partial r} \right) }{2\mu r^2} | R_{3,2} (r) \rangle = \langle Y^{0}_2 (\theta , \phi) | -\hbar^2 \left(\dfrac{\partial^2}{\partial \theta^2}+\text{cot}{\theta}\dfrac{\partial}{\partial \theta}+\dfrac{1}{\sin^2{\theta}}\dfrac{\partial^2}{\partial\phi^2}\right) | Y^{0}_2 (\theta , \phi) \rangle \langle R_{3,2} (r) | \dfrac{ \dfrac{\partial}{\partial r} \left( r^2 \dfrac{\partial}{\partial r} \right) }{2\mu r^2} | R_{3,2} (r) \rangle\]

Spherical part:

\[\langle Y^{0}_2 (\theta , \phi) | -\hbar^2 \left(\dfrac{\partial^2}{\partial \theta^2}+\text{cot}{\theta}\dfrac{\partial}{\partial \theta}+\dfrac{1}{\sin^2{\theta}}\dfrac{\partial^2}{\partial\phi^2}\right) | Y^{0}_2 (\theta , \phi) \rangle = \int_{0}^{\pi} \int_{0}^{ 2 \pi} \sqrt{\dfrac{5}{16\pi}}(3cos^2 \theta - 1) (-\hbar^2 \left(\dfrac{\partial^2}{\partial \theta^2}+\text{cot}{\theta}\dfrac{\partial}{\partial \theta}+\dfrac{1}{\sin^2{\theta}}\dfrac{\partial^2}{\partial\phi^2}\right) ) \sqrt{\dfrac{5}{16\pi}}(3cos^2 \theta - 1) sin \theta d \theta d \phi = \\ \int_{0}^{\pi} \int_{0}^{ 2 \pi} \sqrt{\dfrac{5}{16\pi}}(3cos^2 \theta - 1) (-\hbar^2 \left(\dfrac{\partial^2}{\partial \theta^2}\right) ) \sqrt{\dfrac{5}{16\pi}}(3cos^2 \theta - 1) sin \theta d \theta d \phi + \int_{0}^{\pi} \int_{0}^{ 2 \pi} \sqrt{\dfrac{5}{16\pi}}(3cos^2 \theta - 1) (-\hbar^2 \left(\text{cot}{\theta}\dfrac{\partial}{\partial \theta}\right) ) \sqrt{\dfrac{5}{16\pi}}(3cos^2 \theta - 1) sin \theta d \theta d \phi + \int_{0}^{\pi} \int_{0}^{ 2 \pi} \sqrt{\dfrac{5}{16\pi}}(3cos^2 \theta - 1) (-\hbar^2 \left(\dfrac{1}{\sin^2{\theta}}\dfrac{\partial^2}{\partial\phi^2}\right) ) \sqrt{\dfrac{5}{16\pi}}(3cos^2 \theta - 1) sin \theta d \theta d \phi \]

Radial part:

\[ \langle R_{3,2} (r) | \dfrac{1}{2\mu r^2} | R_{3,2} (r) \rangle = \int_{0}^{\infty} \dfrac{4}{81 \sqrt{30}} \left (\dfrac {Z}{a_0} \right) ^{3/2} \left (\dfrac {Zr}{a_0} \right) ^{2} e^{\dfrac{-Zr}{3a_0}} \dfrac{ -\hbar^2 \dfrac{\partial}{\partial r} \left( r^2 \dfrac{\partial}{\partial r} \right) }{2\mu r^2} \dfrac{4}{81 \sqrt{30}} \left (\dfrac {Z}{a_0} \right) ^{3/2} \left (\dfrac {Zr}{a_0} \right) ^{2} e^{\dfrac{-Zr}{3a_0}} r^2 dr \]

Alternatively:

\[ \hat{KE} = \dfrac{-\hbar^2 \left[ \dfrac{\partial}{\partial r} \left( r^2 \dfrac{\partial}{\partial r} \right) + \dfrac{1}{\sin{\theta}}\dfrac{\partial}{\partial \theta} \left(\sin{\theta}\dfrac{\partial}{\partial \theta}\right)+\dfrac{1}{\sin^2{\theta}}\dfrac{\partial^2}{\partial\phi^2}\right]}{2\mu r^2} = \dfrac{-\hbar^2 \left[ \dfrac{\partial}{\partial r} \left( r^2 \dfrac{\partial}{\partial r} \right) \right]}{2\mu r^2} + \dfrac{-\hbar^2 l(l+1)}{2\mu r^2} \]

b. \[ \hat{PE} = \dfrac{-kZe^2}{r} \]

\[ \langle \hat{PE} \rangle = \langle \psi_{320} (r, \theta , \phi) | \hat{PE} |\psi_{320} (r, \theta , \phi) \rangle = \langle \psi_{320} (r, \theta , \phi) | \dfrac{-kZe^2}{r} |\psi_{320} (r, \theta , \phi) \rangle = \langle R_{3,2} (r) Y^{0}_2 (\theta , \phi) | \dfrac{-kZe^2}{r} | R_{3,2} (r) Y^{0}_2 (\theta , \phi) \rangle = \langle Y^{0}_2 (\theta , \phi) | Y^{0}_2 (\theta , \phi) \rangle \langle R_{3,2} (r) | \dfrac{-kZe^2}{r} | R_{3,2} (r) \rangle = \\ 1 \times \langle R_{3,2} (r) | \dfrac{-kZe^2}{r} | R_{3,2} (r) \rangle = \int_{0}^{\infty} ( \dfrac {1}{81 \sqrt {30}}\left (\dfrac {Z}{a_0} \right ) ^{3/2}( \dfrac {Zr}{a_0}) ^2 e^{-\dfrac {Zr}{3a_0}} )^2 \dfrac{-kZe^2}{r} r^2 dr = \dfrac {1}{81^2 \times 30} (-kZe^2) \int_{0}^{\infty} \left (\dfrac {Z}{a_0} \right ) ^{3} ( \dfrac {Zr}{a_0}) ^4 e^{-\dfrac {2Zr}{3a_0}} r dr = \dfrac {1}{81^2 \times 30} (-kZe^2) \left (\dfrac {a_0}{Z} \right ) \int_{0}^{\infty} \left (\dfrac {Zr}{a_0} \right ) ^{5} e^{-\dfrac {2Zr}{3a_0}} dr = \dfrac {1}{81^2 \times 30} (-kZe^2) \left (\dfrac {a_0}{Z} \right ) ^{2} \dfrac{5!}{(\frac{2}{3})^{5+1}} = \dfrac {1}{81^2 \times 30} (-kZe^2) \left (\dfrac {a_0}{Z} \right ) ^{2} \dfrac{120 \times 3^6 }{2^6} = \dfrac {1}{81^2 \times 30} (-kZe^2) \left (\dfrac {a_0}{Z} \right ) ^{2} \dfrac{120 \times 729 }{64} = (-kZe^2) \left (\dfrac {a_0}{Z} \right ) ^{2} \dfrac{120 \times 729 }{81^2 \times 30 \times 64} = (-kZe^2) \left (\dfrac {a_0}{Z} \right ) ^{2} \dfrac{4 \times 9 }{81 \times 64} =(-kZe^2) \left (\dfrac {a_0}{Z} \right ) ^{2} \dfrac{1 \times 1 }{9 \times 16} = - \dfrac{1}{144} kZe^2 \left(\dfrac {a_0}{Z} \right ) ^{2} = - kZe^2 \dfrac{1}{144} \left (\dfrac {a_0}{Z} \right ) ^{2} = - \dfrac{1}{144} \dfrac {k a_0^2 e^2}{Z} \]

If you did point b. before a. you could use the following approach (to avoid calculation of complicated integrals in point a.):

\(E=KE+PE\), therefore, \(KE=E-PE\).

General expression for total energy (\(E\)) of hydrogen atom:

\[ E_n = - \dfrac {\mu e^4}{8 \epsilon ^2_0 h^2 n^2} \]

In this case energy is:

\[ E_3 = - \dfrac {\mu e^4}{8 \epsilon ^2_0 h^2 3^2} = - \dfrac {\mu e^4}{8 \epsilon ^2_0 h^2 9} = - \dfrac {\mu e^4}{72 \epsilon ^2_0 h^2} \]

Returning to the expression for kinetic energy via total energy:

\(KE=E-PE = - \dfrac {\mu e^4}{72 \epsilon ^2_0 h^2} - \dfrac{-kZe^2}{r} = - \dfrac {\mu e^4}{72 \epsilon ^2_0 h^2} + \dfrac{kZe^2}{r}\)

\(\langle \hat{KE} \rangle = E - \langle \hat{PE} \rangle = - \dfrac {\mu e^4}{72 \epsilon ^2_0 h^2} - kZe^2 \dfrac{1}{144} \left (\dfrac {a_0}{Z} \right ) ^{2} = - \dfrac {\mu e^4}{72 \epsilon ^2_0 h^2} - kZe^2 \dfrac{1}{144} \left (\dfrac {a_0}{Z} \right ) ^{2} \)

c. General expression for virial theorem:

\(2KE=nPE\), where n is the power of \(r\) in the general expression for potential energy \(PE(r)=ar^n\)

Since in the expression for (\(PE=\dfrac{-kZe^2}{r} \)) \(r\) is in -1 power, then virial theorem in this case is \(2KE=-1PE\).

Q8

How many angular and radial nodes are there for the following hydrogenic orbitals/wavefunctions?

1. \( \psi_{320} (r,\theta, \phi ) \)
2. \( \psi_{3s} (r,\theta, \phi ) \)
3. \( \psi_{2p_y} (r,\theta, \phi ) \)

# Angular Nodes \( = \ell \)

# Radial Nodes \( = n -1 - \ell \)

a. # Angular Nodes \( = \ell = 2\)

# Radial Nodes \( = n -1 - \ell = 3-1-2=0 \)

b. # Angular Nodes \( = \ell = 0\)

# Radial Nodes \( = n -1 - \ell = 3-1-0=2 \)

c. # Angular Nodes \( = \ell = 1\)

# Radial Nodes \( = n -1 - \ell = 2-1-1=0 \)

Q9

For the following H orbitals, locate the radial and angular nodes.

1. \( \psi_{1s} (r,\theta, \phi ) \)
2. \( \psi_{2s} (r,\theta, \phi ) \)
3. \( \psi_{2p_x} (r,\theta, \phi ) \)
4. \( \psi_{2p_y} (r,\theta, \phi ) \)
5. \( \psi_{2p_z} (r,\theta, \phi ) \)
6. \( \psi_{3s} (r,\theta, \phi ) \)
7. \( \psi_{3p_x} (r,\theta, \phi ) \)

Use radial functions \(R(r)\) and spherical harmonics \(Y (\theta, \phi)\) (or linear combinations of \(Y (\theta, \phi)\)) corresponding to the \( \psi\) in question from the tables. Find \(r \)'s for radial nodes and (\(\theta , \phi \)) pairs for angular nodes that turn \(R(r)\) and \(Y (\theta, \phi)\), respectively into zeros. Make sure your number of zeros or nodes (\(r\)'s and (\(\theta , \phi \)) pairs) matches the number predicted by the formulas:

# Radial Nodes \( = n -1 - \ell \)

# Angular Nodes \( = \ell \)

Remember, \(r=0\) is not considered a node, \(\theta \in [0,\pi] \) and \(\phi \in [0,2\pi] \).

1. \( \psi_{1s} (r,\theta, \phi ) = \psi_{100}= R_{1,0} (r) Y_0^{0} (\theta , \phi) \)

\(R_{1,0} (r) = 2 \left (\dfrac {Z}{a_0} \right ) ^{3/2} e^{- \dfrac {Zr}{a_0}} \) has no zeros or nodes.

\(Y_0^{0} (\theta , \phi)= \dfrac {1}{\sqrt {4 \pi}}\) has no zeros or nodes.

# Radial Nodes \( = n -1 - \ell = 1-1-0=0\)

# Angular Nodes \( = \ell =0\)

2. \( \psi_{2s} (r,\theta, \phi ) = \psi_{200}= R_{2,0} (r) Y_0^{0} (\theta , \phi)\)

\(R_{2,0} (r) = \dfrac {1}{2 \sqrt {2}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} (2 - \dfrac {Zr}{a_0}) e^{-\dfrac {Zr}{2a_0}} \) is zero when \((2 - \dfrac {Zr}{a_0}) = 0 \). Therefore, node is at \(r=\dfrac {2a_0}{Z}\).

\(Y_0^{0} (\theta , \phi)= \dfrac {1}{\sqrt {4 \pi}}\) has no zeros or nodes.

# Radial Nodes \( = n -1 - \ell = 2-1-0=1\)

# Angular Nodes \( = \ell =0\)

3. \( \psi_{2p_x} (r,\theta, \phi ) = \dfrac{1}{\sqrt{2}} (\psi_{21−1} − \psi_{211}) = \dfrac{1}{\sqrt{2}} (R_{2,1}(r)Y_1^{-1}(\theta , \phi) − R_{2,1}(r)Y_1^{1}(\theta , \phi)) = \dfrac{1}{\sqrt{2}} R_{2,1}(r)(Y_1^{-1}(\theta , \phi) − Y_1^{1}(\theta , \phi)) \)

\(R_{2,1} (r) = \dfrac {1}{2 \sqrt {6}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} \dfrac {Zr}{a_0} e^{-\dfrac {Zr}{2a_0}} \) has zero when \(r=0\), however, this is not a node.

\(\dfrac{1}{\sqrt{2}} (Y_1^{-1}(\theta , \phi) − Y_1^{1}(\theta , \phi)) = \dfrac{1}{\sqrt{2}} ( \sqrt {\dfrac {3}{8 \pi}}\sin \theta e^{-i \phi} - \sqrt {\dfrac {3}{8 \pi}}\sin \theta e^{i \phi})= \dfrac{1}{\sqrt{2}} \sqrt {\dfrac {3}{8 \pi}} \sin \theta (e^{-i \phi} - e^{i \phi}) = \\ \dfrac{1}{\sqrt{2}} \sqrt {\dfrac {3}{8 \pi}} \sin \theta (-2i) \dfrac{e^{i \phi} - e^{-i \phi}}{2i} = \dfrac{1}{\sqrt{2}} \sqrt {\dfrac {3}{8 \pi}} \sin \theta (-2i) \sin{\phi} \)

is zero when either \(\sin \theta = 0\) or \(\sin \phi = 0\). Therefore, \(\theta = 0 \ or \ \pi\) and \(\phi = 0 \ or \ \pi \).

# Radial Nodes \( = n -1 - \ell = 2-1-1=0\)

# Angular Nodes \( = \ell =1\)

4. \( \psi_{2p_y} (r,\theta, \phi ) = - \dfrac{i}{\sqrt{2}} (\psi_{21−1} + \psi_{211}) = - \dfrac{i}{\sqrt{2}} (R_{2,1}(r)Y_1^{-1}(\theta , \phi) + R_{2,1}(r)Y_1^{1}(\theta , \phi)) = - \dfrac{i}{\sqrt{2}} R_{2,1}(r)(Y_1^{-1}(\theta , \phi) + Y_1^{1}(\theta , \phi)) \)

\(R_{2,1} (r) = \dfrac {1}{2 \sqrt {6}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} \dfrac {Zr}{a_0} e^{-\dfrac {Zr}{2a_0}} \) has zero when \(r=0\), however, this is not a node.

\(-\dfrac{i}{\sqrt{2}} (Y_1^{-1}(\theta , \phi) + Y_1^{1}(\theta , \phi)) = - \dfrac{i}{\sqrt{2}} ( \sqrt {\dfrac {3}{8 \pi}}\sin \theta e^{-i \phi} + \sqrt {\dfrac {3}{8 \pi}}\sin \theta e^{i \phi})= - \dfrac{i}{\sqrt{2}} \sqrt {\dfrac {3}{8 \pi}} \sin \theta (e^{-i \phi} + e^{i \phi}) = \\ - \dfrac{i}{\sqrt{2}} \sqrt {\dfrac {3}{8 \pi}} \sin \theta \ 2 \ \dfrac{e^{-i \phi} + e^{i \phi}}{2} = - \dfrac{i}{\sqrt{2}} \sqrt {\dfrac {3}{8 \pi}} \sin \theta \ 2 \ \cos \phi \)

is zero when either \(\sin \theta = 0\) or \(\cos \phi = 0\). Therefore, \(\theta = 0 \ or \ \pi\) and \(\phi = \dfrac{\pi}{2} \ or \ \dfrac{3\pi}{2} \).

# Radial Nodes \( = n -1 - \ell = 2-1-1=0\)

# Angular Nodes \( = \ell =1\)

5. \( \psi_{2p_z} (r,\theta, \phi ) = \psi_{210} = R_{2,1}(r)Y_1^{0}(\theta , \phi) \)

\(R_{2,1} (r) = \dfrac {1}{2 \sqrt {6}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} \dfrac {Zr}{a_0} e^{-\dfrac {Zr}{2a_0}} \) has zero when \(r=0\), however, this is not a node.

\(Y_1^{0}(\theta , \phi)= \sqrt {\dfrac {3}{4 \pi}}\cos \theta\) is zero when \(\cos \theta = 0\). Therefore, \(\theta = \dfrac{\pi}{2}\).

# Radial Nodes \( = n -1 - \ell = 2-1-1=0\)

# Angular Nodes \( = \ell =1\)

6. \( \psi_{3s} (r,\theta, \phi ) = \psi_{300} = R_{3,0}(r)Y_0^{0}(\theta , \phi) \)

\(R_{3,0} (r) =\dfrac {1}{81 \sqrt {3}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} (27 - 18 \dfrac {Zr}{a_0} + 2(\dfrac {Zr}{a_0})^2) e^{-\dfrac {Zr}{3a_0}} \) has zeros when \(27 - 18 \dfrac {Zr}{a_0} + 2(\dfrac {Zr}{a_0}) ^2 = 0\). The roots of the quadratic equation are \(\dfrac {Zr}{a_0} = \dfrac{9 \pm 3 \sqrt{3}}{2}\). Therefore, \(r = \dfrac {a_0}{Z} \dfrac{9 \pm 3 \sqrt{3}}{2}\).

\(Y_0^{0} (\theta , \phi)= \dfrac {1}{\sqrt {4 \pi}}\) has no zeros or nodes.

# Radial Nodes \( = n -1 - \ell = 3-1-0=2\)

# Angular Nodes \( = \ell =0\)

7. \( \psi_{3p_x} (r,\theta, \phi ) = \dfrac{1}{\sqrt{2}} (\psi_{31−1} − \psi_{311}) = \dfrac{1}{\sqrt{2}} (R_{3,1}(r)Y_1^{-1}(\theta , \phi) − R_{3,1}(r)Y_1^{1}(\theta , \phi)) = \dfrac{1}{\sqrt{2}} R_{3,1}(r)(Y_1^{-1}(\theta , \phi) − Y_1^{1}(\theta , \phi))\)

\(R_{3,1} (r) = \dfrac {1}{81 \sqrt {6}}\left (\dfrac {Z}{a_0} \right ) ^{3/2} (6 \dfrac {Zr}{a_0} - \left (\dfrac {Zr}{a_0} \right )^2) e^{-\dfrac {Zr}{3a_0}} \) has zero when \(6 \dfrac {Zr}{a_0} - \left (\dfrac {Zr}{a_0} \right )^2 = 0\) or \(\dfrac {Zr}{a_0} (6- \dfrac {Zr}{a_0}) = 0\). This is true when \(r=0\) or \(r= \dfrac {6a_0}{Z}\). Only \(r= \dfrac {6a_0}{Z}\) is a node.

\(\dfrac{1}{\sqrt{2}} (Y_1^{-1}(\theta , \phi) − Y_1^{1}(\theta , \phi)) = \dfrac{1}{\sqrt{2}} ( \sqrt {\dfrac {3}{8 \pi}}\sin \theta e^{-i \phi} - \sqrt {\dfrac {3}{8 \pi}}\sin \theta e^{i \phi})= \dfrac{1}{\sqrt{2}} \sqrt {\dfrac {3}{8 \pi}} \sin \theta (e^{-i \phi} - e^{i \phi}) = \\ \dfrac{1}{\sqrt{2}} \sqrt {\dfrac {3}{8 \pi}} \sin \theta (-2i) \dfrac{e^{i \phi} - e^{-i \phi}}{2i} = \dfrac{1}{\sqrt{2}} \sqrt {\dfrac {3}{8 \pi}} \sin \theta (-2i) \sin{\phi} \)

is zero when either \(\sin \theta = 0\) or \(\sin \phi = 0\). Therefore, \(\theta = 0 \ or \ \pi\) and \(\phi = 0 \ or \ \pi \).

# Radial Nodes \( = n -1 - \ell = 3-1-1=1\)

# Angular Nodes \( = \ell =1\)

Q10

Use Slater's rules to calculate \(Z_{eff}\) and \(Z\) for

1. The valence electron of the Neon atom
2. The the innermost electron of Beryllium atom
3. The \(4s^2\) electrons of the I atom
4. The outermost electron of the row 2 elemental atom with the largest effective nuclear charge

1. The valence electron of the Neon atom

(1s²) (2s² 2p⁶)

S = 0.35x7+0.85x2 = 4.15

Zeff = Z-S = 10-4.15 = 5.85

b. The the innermost electron of Lithium atom

(1s²) (2s¹)

S = 0.3x1 = 0.3

Zeff = Z-S = 3-0.3 = 2.7

c. The \(4s^2\) electrons of the Br atom

(1s²) (2s² 2p⁶) (3s² 3p⁶) (3d¹⁰) (4s² 4p⁵)

S = 0.35x6+0.85x18+1.00x10 = 27.4

Zeff = Z-S = 35-27.4= 7.6

d. The outermost electron of the row 2 elemental atom with the largest effective nuclear charge

Ne

(1s²) (2s² 2p⁶)

S = 0.35x7+0.85x2 = 4.15

Zeff = Z-S = 10-4.15 = 5.85

Q11

Evaluate the trial energy of the unnormalized trial function

\[ | \varphi \rangle = x(L−x) \rangle \]

to estimate the ground state energy for a particle in a one-dimensional box of length \(L\). (Hint: If you want the general pain, you can find this answer in this paper, but it is not necessary). You are not minimizing a parameter in this question.

From variational method:

\[E_1 \leq \dfrac{\langle\varphi | H | \varphi\rangle}{\langle\varphi |\varphi\rangle} \]

To get the upper limit for \(E_1\) from variational method we need to calculate the following integral:

\[\dfrac{\langle\varphi| H | \varphi\rangle}{\langle\varphi |\varphi\rangle} \]

First we must normalize \(\varphi\) by calculating the denominator integral:

\[\langle\varphi | \varphi\rangle= \int_{0}^{L}x^2(L-x)^2dx =\int_{0}^{L}(x^2 L^2 -2Lx^3 +x^4)dx = \\ (L^2\dfrac{x^3}{3}\Biggr\rvert_{0}^{L} - 2L\dfrac{x^4}{4} \Biggr\rvert_{0}^{L}+ \dfrac{x^5}{5}\Biggr\rvert_{0}^{L}) = (\dfrac{L^5}{3} - \dfrac{2L^5}{4} + \dfrac{L^5}{5}) = \dfrac{(10-15+6)L^5}{30}= \dfrac{L^5}{30}\]

Then we calculate the numerator:

\[\langle\varphi | H | \varphi\rangle = \int_{0}^{L}x(L−x) (- \dfrac{\hbar^2}{2m}\dfrac{d^2}{dx^2}) x(L−x)dx = \\- \dfrac{\hbar^2}{2m} \int_{0}^{L} (xL - x^2) (-2) dx = \dfrac{\hbar^2}{m} (L\dfrac{x^2}{2} - \dfrac{x^3}{3}) \Biggr\rvert_{0}^{L} = \dfrac{\hbar^2}{m} (\dfrac{L^3}{2} - \dfrac{L^3}{3}) = \dfrac{\hbar^2}{m} \dfrac{L^3(3-2)}{6} = \dfrac{\hbar^2 L^3}{6m} \]

Plug the numerator and denominator in the initial expression:

\[\dfrac{\langle\varphi| H | \varphi\rangle}{\langle\varphi |\varphi\rangle} = \dfrac{\dfrac{\hbar^2 L^3}{6m}}{ \dfrac{L^5}{30}} = \dfrac{30}{L^5} \dfrac{\hbar^2 L^3}{6m} = \dfrac{5\hbar^2}{mL^2}\]

The conclusion is:

\[E_1 \leq \dfrac{5\hbar^2}{mL^2}\]

Q12

How would use the variational method approximation in Q11 to determined the energy of the next highest eigenstate for the particle in a box with \(n=2\)?

Variational method cannot be used for excited states. We need to use other theories (e.g., perturbation).

Q13

Consider the "quartic oscillator" with the following Hamiltonian

\[ \hat{H} = \dfrac{1}{2} \dfrac{d^2}{dx^2} + \dfrac{1}{2} x^4\]

1. What is the zero point energy of this this system determined with the variational method approximation using the unnormalized trial wavefunction \[ | \varphi \rangle = e^{-\dfrac{1}{2} \alpha (x-x_o)^2} \]
2. What is the value of \(\alpha\) for the trial wavefunction used in this approximation?
3. How accurate would this wavefunction be in estimating the zero point energy of the harmonic oscillator?

a. What is the zero point energy of this this system determined with the variational method approximation using the unnormalized trial wavefunction \[ | \varphi \rangle = e^{-1/2 \alpha (x-x_o)^2} \]

To simplify calculations we will use displacement coordinate \(q\) instead of \((x-x_o)\).

Then, analogously to the solution in Q2:

\[E_0 \leq \dfrac{\langle\varphi | H | \varphi\rangle}{\langle\varphi |\varphi\rangle} \]

Normalization by calculating the denominator:

\[\langle\varphi | \varphi\rangle= \int_{-\infty}^{\infty} e^{- \alpha q^2} dq = \sqrt{\dfrac{\pi}{\alpha}} \]

Numerator:

\[\langle\varphi | H | \varphi\rangle = \int_{-\infty}^{\infty} e^{-\dfrac{1}{2} \alpha q^2} (\dfrac{1}{2} \dfrac{d^2}{dq^2} + \dfrac{1}{2} q^4) e^{-\dfrac{1}{2} \alpha q^2} dq = \\ \int_{-\infty}^{\infty} e^{-\dfrac{1}{2} \alpha q^2} (\dfrac{1}{2} (-\alpha + \alpha^2 q^2)e^{-\dfrac{1}{2} \alpha q^2} + \dfrac{1}{2} q^4 e^{-\dfrac{1}{2} \alpha q^2}) dq = \\ \int_{-\infty}^{\infty} e^{-\dfrac{1}{2} \alpha q^2} \dfrac{1}{2} (-\alpha + \alpha^2 q^2)e^{-\dfrac{1}{2} \alpha q^2} dq + \int_{-\infty}^{\infty} e^{-\dfrac{1}{2} \alpha q^2} \dfrac{1}{2} q^4 e^{-\dfrac{1}{2} \alpha q^2} dq = \\ \dfrac{1}{2} (\int_{-\infty}^{\infty} e^{-\alpha q^2} (-\alpha + \alpha^2 q^2) dq + \int_{-\infty}^{\infty} e^{-\alpha q^2} q^4 dq) = \\ \dfrac{1}{2} (-\alpha \int_{-\infty}^{\infty} e^{-\alpha q^2} dq + \alpha^2 \int_{-\infty}^{\infty} q^2 e^{-\alpha q^2} dq + \int_{-\infty}^{\infty} e^{-\alpha q^2} q^4 dq) = \\ \dfrac{1}{2} (-\alpha \sqrt{\dfrac{\pi}{\alpha}} + \alpha^2 \dfrac{1}{2}\sqrt{\dfrac{\pi}{ \alpha^3}} + \dfrac{3}{4} \sqrt{\dfrac{\pi}{\alpha^5}})\]

\[\dfrac{\langle\varphi | H | \varphi\rangle}{\langle\varphi |\varphi\rangle} = \sqrt{\dfrac{\alpha}{\pi}} (- \dfrac{1}{2} \alpha \sqrt{\dfrac{\pi}{\alpha}} + \dfrac{1}{2} \alpha^2 \dfrac{1}{2} \sqrt{\dfrac{\pi}{\alpha^3}} + \dfrac{1}{2}\dfrac{3}{4} \sqrt{\dfrac{\pi}{\alpha^5}})= \\ -\dfrac{1}{2} \alpha + \dfrac{1}{4} \alpha + \dfrac{3}{8} \dfrac{1}{\alpha^2} = I \]

b. What is the value of \(\alpha\) for the trail wavefunction used in this approximation?

Optimal \(\alpha\) is found by taking the derivative of \(I\) and calculating the \(\alpha\) at which the derivative is equal to zero:

\[ \dfrac{dI}{d \alpha} = -\dfrac{1}{2} + \dfrac{1}{4} - \dfrac{3}{4} \dfrac{1}{\alpha^3} = 0 \]

\[\alpha = - 3^{1/3}\]

c. How accurate would this wavefunction be in estimating the zero point energy of the harmonic oscillator?

The normalized trial wavefunction \( | \varphi \rangle = (\dfrac{\alpha}{\pi})^{1/4} e^{-1/2 \alpha (x-x_o)^2} \) has the same structure as the true wavefunction of the ground state of harmonic oscillator \(| \psi_0 \rangle = \pi^{-1/4} e^{-1/2(x-x_o)^2}\). The functions are equal when \(\alpha = 1\). Thus, the trial wavefunction would be accurate in estimating the zero point energy of the harmonic oscillator.

Q14

A basis function is an element of a particular basis for a function space. Every continuous function in the function space can be represented as a linear combination of basis functions, just as every vector in a vector space can be represented as a linear combination of basis vectors.

• List three basis that can be used to expand a general 1-D function.
• Write the mathematical expansion formula for each of the three expansions above

Laplace Series Expansion

\[f(x) = \sum_s^\infty A_s e^{-st}\]

Fourier Series Expansion

\[f(x) = a_0 + \sum_n^\infty a_ncosnx + b_nsinnx\]

Taylor Series Expansion

\[f(x) = \sum_n^\infty \frac{f^{(n)}(a)}{n!}(x - a)^n\]

Q15

What is the definition of a complete basis? Are the three basis systems identified above complete basis for describing 1-D functions?

A set of functions is considered complete if all other functions can be expressed in terms of them. All the expansions from part 1 are complete.

Q16

What are the following dot products for the particle in a box?

1. \(\langle \psi_{n=1} | \psi_{n=1} \rangle \)
2. \(\langle \psi_{n=1} | \psi_{n=2} \rangle \)
3. \(\langle \psi_{n=2} | \psi_{n=1} \rangle \)
4. \(\langle \psi_{n=2} | \psi_{n=2} \rangle \)

Particle in a box wavefunctions are orthonormal. This means their dot product (\(\langle \psi_{i} | \psi_{j} \rangle \)) is 0 when \(i \neq j \) and 1 when \(i=j\).

Alternatively, you can show it by evaluating the integrals:

\[ |\psi_1 \rangle = (\frac{2}{L})^{\frac{1}{2}}sin\frac{\pi x}{L}\]

\[ |\psi_2 \rangle = (\frac{2}{L})^{\frac{1}{2}}sin\frac{2\pi x}{L}\]

\[\langle \psi_1 |\psi_1 \rangle = \int \limits _{-\infty}^{\infty} \frac{2}{L}(sin\frac{\pi x}{L})^2 dx = 1\]

\[\langle \psi_2 |\psi_1 \rangle = \int \limits _{-\infty}^{\infty} \frac{2}{L}(sin\frac{2\pi x}{L})(sin\frac{\pi x}{L}) dx = 0\]

\[\langle \psi_1 |\psi_2 \rangle = \int \limits _{-\infty}^{\infty} \frac{2}{L}(sin\frac{\pi x}{L})(sin\frac{2\pi x}{L}) dx = 0\]

\[\langle \psi_2 |\psi_2 \rangle = \int \limits _{-\infty}^{\infty} \frac{2}{L}(sin\frac{2\pi x}{L})^2 dx = 1\]

Q17

The wavefunction can be expanded into the complete set of basis of eigenstates of the Hamiltonian:

\[| \Psi \rangle =\sum_i c_i | \phi_i \rangle \]

What is the general expression of the off diagonal (\(i \neq j\)) and diagonal (\(i = j\)) matrix elements for the Hamiltonian in the basis set of its eigenstates?

\[H_{ij} = \langle \phi_i | \hat{H} | \phi_j \rangle \]

(hint: Apply the Hamiltonian \(\hat{H}\) on this arbitrary wavefuction \(| \Psi \rangle\) and its bra version \(\langle \Psi | \)).

\[H_{ij} = \langle \phi_i |c_i \hat{H} c_j | \phi_j \rangle = (c_i^* \times c_j)E_j \langle \phi_i | \phi_j \rangle\ = 0\]

Here, we used the general expression for time-independent Schrodinger equation (without specifying \(\hat{H}\)) : \(\hat{H} \phi_j = E_j \phi_j\), substituted \(E_j \phi_j\) for \(\hat{H} \phi_j \) and pulled the constants \( c_i^* \ and \ c_j) \) out of the integral. Because \(\phi_i\) and \(\phi_j\) are orthogonal we get \(\langle \phi_i | \phi_j \rangle\ = 0\) and \(H_{ij} =0\).

\[H_{ii} = \langle \phi_i |c_i \hat{H} c_i | \phi_i \rangle =c_i^* c_i E_i \langle \phi_i | \phi_i \rangle\ = |c_i^2|E_i \langle \phi_i | \phi_i \rangle\ = E_i\]

Here, we also used the general expression for time-independent Schrodinger equation (without specifying \(\hat{H}\)) : \(\hat{H} \phi_i = E_i \phi_i \), substituted \(E_i \phi_i\) for \(\hat{H} \phi_i \) and pulled the constants \( c_i^* \ and \ c_i) \) out of the integral. Because \(\phi_i\) is normalized we get \(\langle \phi_i | \phi_i \rangle\ =1\) and \(H_{ii} =E_i\).

Q18

Estimate the ground state energy and wavefunction for a particle in a box using the variational method with the following trial wavefunction, where N is the normalization constant and \(\beta\) is a variational parameter that should be minimized.

\[ | \psi \rangle = N \exp(-\beta x^2)\]

1. Is this a good trial wavefunction for this approximation (justify your answer)?
2. Why is this not a good wavefunction?
3. Can you solve this problem both analytically and numerically? Pay careful attention to limits of integration.

\[E_{trial}= \dfrac{\langle\psi_{trial}| H | \psi_{trial}\rangle}{\langle\psi_{trial} | \psi_{trial} \rangle}\]

\[H = \dfrac{-\hbar^2}{2m} \dfrac{\delta^2}{\delta x^2}\]

\[\langle\psi_{trial}|\psi_{trial}\rangle = \int_{0}^{L} N^2 e^{-2\beta x^2} dx = \int_{-(2\beta)^{1/2}L/2}^{(2\beta)^{1/2}L/2} N^2 (2\beta)^{1/2}e^{-t^2}dt = 1\]

where

• \(t = (2\beta)^{1/2} x\) and
• \(dt = (\beta)^{1/2} dx\)

\[N = (\beta \pi)^{-1/4} \times (erf((2\beta)^{1/2} L))^{-1/2}\]

Where \(erf((2\beta)^{1/2}L\) is the error function evaluated at \((2\beta)^{1/2}L\).

\[ E_{trial} = {\langle\psi_{trial}| H | \psi_{trial}\rangle} = \int_{-(2\beta)^{1/2}L/2}^{(2\beta)^{1/2}L/2} N^2 e^{-\beta x^2} \dfrac{-\hbar}{2m} \dfrac{\delta^2}{\delta x^2} e^{-\beta x^2} dx = \int_{-(2\beta)^{1/2}L/2}^{(2\beta)^{1/2}L/2} N^2 e^{-\beta x^2} \dfrac{-\hbar}{2m} \dfrac{\delta}{\delta x} 2x\beta e^{-\beta x^2} dx\]

\[ = \int_{-(2\beta)^{1/2}L/2}^{(2\beta)^{1/2}L/2} N^2 \beta^{-1/2}e^{-t^2} \dfrac{-\hbar}{2m} (-2\beta e^{-t^2} + 4t^2\beta e^{-t^2})dt\]

\[= -\frac{N^2 \hbar^2}{2m\beta^{1/2}}\left[\left(-2\beta \int_{-(2\beta)^{1/2}L/2}^{(2\beta)^{1/2}L/2}e^{-t^2}dt\right) + \left(2\beta \int_{-(2\beta)^{1/2}L/2}^{(2\beta)^{1/2}L/2}t^2e^-t^2 dt\right)\right]\]

\[= -\frac{N^2 \hbar^2 \beta^{1/2}}{2m}(\frac{L(2\beta)^{1/2}}{2e^{L^22\beta}} - \frac{1}{2}\pi^{1/2}ierfi(\frac{Li(2\beta)^{1/2}}{2}) -(2\beta \pi)^{1/2}erf(\frac{(2\beta)^{1/2}L}{2})))\]

Where erfi is the imaginary error function. So overall we have for the unoptimized ground state energy:

\[E_{trial} = -\frac{(\beta \pi)^{-1/2} \times (erf((2\beta)^{1/2} \frac{L}{2}))^{-1} \hbar^2 \beta^{1/2}}{2m}(-\frac{L(2\beta)^{1/2}}{2e^{\frac{L^2\beta}{2}}} + \frac{1}{2}\pi^{1/2}erf(\frac{-L(2\beta)^{1/2}}{2}) - (2\beta \pi)^{1/2}erf(\frac{(2\beta)^{1/2}L}{2}))\]

Normally to optimize the energy we would take the derivative of our trial energy with respected to beta and find the minimum. Here due to the complexity of the equation an easier solution would be to numerically plot the energy as a function of beta, though to do that we would need to have a value for L.

A) and B) A Gaussian is a poor trial function for a particle in a box since a Gaussian does not go to zero at any values other than infinity. While the box potential has a finite size, if the box potential had infinite size then we would be dealing with a free particle.

C) This problem can be solved up to the unoptimized trial energy analytically but taking the derivative leads to a transcendental equation so it has to be solved numerically.