6.3: Nuclear Radiation
- Last updated
- Save as PDF
- Page ID
- 13192
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Write and balance nuclear equations
- To know the different kinds of radioactive decay.
- To balance a nuclear reaction.
Nuclear chemistry is the study of reactions that involve changes in nuclear structure. The chapter on atoms, molecules, and ions introduced the basic idea of nuclear structure, that the nucleus of an atom is composed of protons and, with the exception of \(\ce{^1_1H}\), neutrons. Recall that the number of protons in the nucleus is called the atomic number (\(Z\)) of the element, and the sum of the number of protons and the number of neutrons is the mass number (\(A\)). Atoms with the same atomic number but different mass numbers are isotopes of the same element. When referring to a single type of nucleus, we often use the term nuclide and identify it by the notation:
\[ \large \ce{^{A}_{Z}X} \label{Eq1a} \]
where
- \(X\) is the symbol for the element,
- \(A\) is the mass number, and
- \(Z\) is the atomic number.
Often a nuclide is referenced by the name of the element followed by a hyphen and the mass number. For example, \(\ce{^{14}_6C}\) is called “carbon-14.”
Protons and neutrons, collectively called nucleons, are packed together tightly in a nucleus. With a radius of about 10−15 meters, a nucleus is quite small compared to the radius of the entire atom, which is about 10−10 meters. Nuclei are extremely dense compared to bulk matter, averaging \(1.8 \times 10^{14}\) grams per cubic centimeter. For example, water has a density of 1 gram per cubic centimeter, and iridium, one of the densest elements known, has a density of 22.6 g/cm3. If the earth’s density were equal to the average nuclear density, the earth’s radius would be only about 200 meters (earth’s actual radius is approximately \(6.4 \times 10^6\) meters, 30,000 times larger).
Changes of nuclei that result in changes in their atomic numbers, mass numbers, or energy states are nuclear reactions. To describe a nuclear reaction, we use an equation that identifies the nuclides involved in the reaction, their mass numbers and atomic numbers, and the other particles involved in the reaction.
Nuclear Equations
A balanced chemical reaction equation reflects the fact that during a chemical reaction, bonds break and form, and atoms are rearranged, but the total numbers of atoms of each element are conserved and do not change. A balanced nuclear reaction equation indicates that there is a rearrangement during a nuclear reaction, but of subatomic particles rather than atoms. Nuclear reactions also follow conservation laws, and they are balanced in two ways:
- The sum of the mass numbers of the reactants equals the sum of the mass numbers of the products.
- The sum of the charges of the reactants equals the sum of the charges of the products.
If the atomic number and the mass number of all but one of the particles in a nuclear reaction are known, we can identify the particle by balancing the reaction. For instance, we could determine that \(\ce{^{17}_8O}\) is a product of the nuclear reaction of \(\ce{^{14}_7N}\) and \(\ce{^4_2He}\) if we knew that a proton, \(\ce{^1_1H}\), was one of the two products. Example \(\PageIndex{1}\) shows how we can identify a nuclide by balancing the nuclear reaction.
Example \(\PageIndex{1}\): Balancing Equations for Nuclear Reactions
The reaction of an α particle with magnesium-25 \( (\ce{^{25}_{12}Mg})\) produces a proton and a nuclide of another element. Identify the new nuclide produced.
Solution
The nuclear reaction can be written as:
\[\ce{^{25}_{12}Mg + ^4_2He \rightarrow ^1_1H + ^{A}_{Z}X} \nonumber \]
where
- \(\ce A\) is the mass number and
- \(\ce Z\) is the atomic number of the new nuclide, \(\ce X\).
Because the sum of the mass numbers of the reactants must equal the sum of the mass numbers of the products:
\[\mathrm{25+4=A+1} \nonumber \]
so
\[ \mathrm{A=28} \nonumber \]
Similarly, the charges must balance, so:
\[\mathrm{12+2=Z+1} \nonumber \]
so
\[\mathrm{Z=13} \nonumber \]
Check the periodic table: The element with nuclear charge = +13 is aluminum. Thus, the product is \(\ce{^{28}_{13}Al}\).
Exercise \(\PageIndex{1}\)
The nuclide \(\ce{^{125}_{53}I}\) combines with an electron and produces a new nucleus and no other massive particles. What is the equation for this reaction?
- Answer
-
\[\ce{^{125}_{53}I + ^0_{−1}e \rightarrow ^{125}_{52}Te} \nonumber \]
The two general kinds of nuclear reactions are nuclear decay reactions and nuclear transmutation reactions. In a nuclear decay reaction, also called radioactive decay, an unstable nucleus emits radiation and is transformed into the nucleus of one or more other elements. The resulting daughter nuclei have a lower mass and are lower in energy (more stable) than the parent nucleus that decayed. In contrast, in a nuclear transmutation reaction, a nucleus reacts with a subatomic particle or another nucleus to form a product nucleus that is more massive than the starting material. As we shall see, nuclear decay reactions occur spontaneously under all conditions, but nuclear transmutation reactions occur only under very special conditions, such as the collision of a beam of highly energetic particles with a target nucleus or in the interior of stars. We begin this section by considering the different classes of radioactive nuclei, along with their characteristic nuclear decay reactions and the radiation they emit.
Nuclear decay reactions occur spontaneously under all conditions, whereas nuclear transmutation reactions are induced.
Nuclear Decay Reactions
Just as we use the number and type of atoms present to balance a chemical equation, we can use the number and type of nucleons present to write a balanced nuclear equation for a nuclear decay reaction. This procedure also allows us to predict the identity of either the parent or the daughter nucleus if the identity of only one is known. Regardless of the mode of decay, the total number of nucleons is conserved in all nuclear reactions.
To describe nuclear decay reactions, chemists have extended the \(^A _Z \textrm{X}\) notation for nuclides to include radioactive emissions. Table \(\PageIndex{1}\) lists the name and symbol for each type of emitted radiation. The most notable addition is the positron, a particle that has the same mass as an electron but a positive charge rather than a negative charge.
| Identity | Symbol | Charge | Mass (amu) |
|---|---|---|---|
| helium nucleus | \(^4_2\alpha\) | +2 | 4.001506 |
| electron | \(^0_{-1}\beta\) or \(\beta ^-\) | −1 | 0.000549 |
| photon | \(_0^0\gamma\) | — | — |
| neutron | \(^1_0\textrm n\) | 0 | 1.008665 |
| proton | \(^1_1\textrm p \) | +1 | 1.007276 |
| positron | \(^0_{+1}\beta\) or \(\beta ^+\) | +1 | 0.000549 |
Like the notation used to indicate isotopes, the upper left superscript in the symbol for a particle gives the mass number, which is the total number of protons and neutrons. For a proton or a neutron, A = 1. Because neither an electron nor a positron contains protons or neutrons, its mass number is 0. The numbers should not be taken literally, however, as meaning that these particles have zero mass; ejection of a beta particle (an electron) simply has a negligible effect on the mass of a nucleus.
Similarly, the lower left subscript gives the charge of the particle. Because protons carry a positive charge, Z = +1 for a proton. In contrast, a neutron contains no protons and is electrically neutral, so Z = 0. In the case of an electron, Z = −1, and for a positron, Z = +1. Because γ rays are high-energy photons, both A and Z are 0. In some cases, two different symbols are used for particles that are identical but produced in different ways. For example, the symbol \(^0_{-1}\textrm e\), which is usually simplified to e−, represents a free electron or an electron associated with an atom, whereas the symbol \(^0_{-1}\beta\), which is often simplified to β−, denotes an electron that originates from within the nucleus, which is a β particle. Similarly, \(^4_{2}\textrm{He}^{2+}\) refers to the nucleus of a helium atom, and \(^4_{2}\alpha\) denotes an identical particle that has been ejected from a heavier nucleus.
There are six fundamentally different kinds of nuclear decay reactions, and each releases a different kind of particle or energy. The essential features of each reaction are shown in Figure \(\PageIndex{1}\). The most common are alpha and beta decay and gamma emission, but the others are essential to an understanding of nuclear decay reactions.
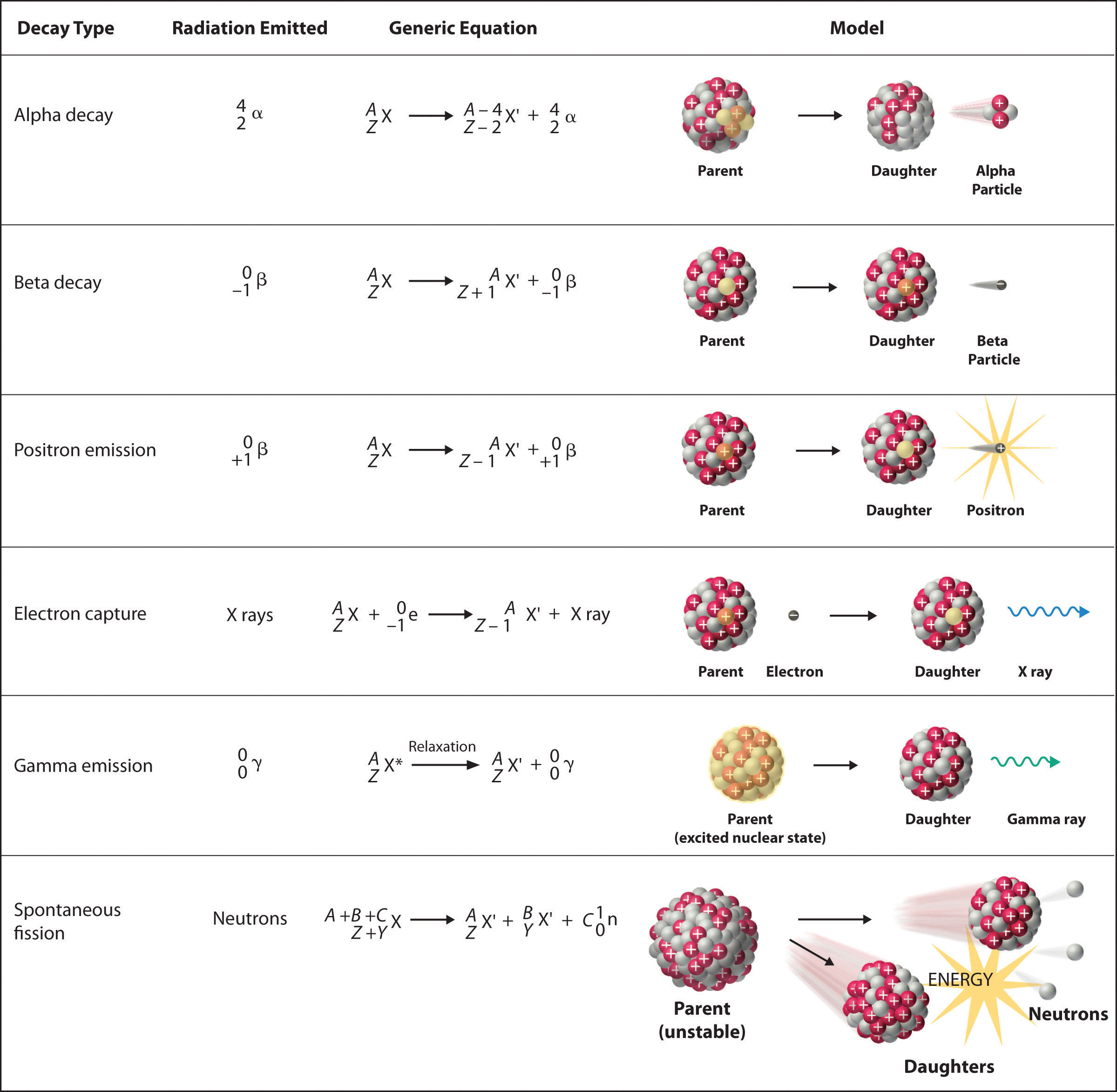
Alpha \(\alpha\) Decay
Many nuclei with mass numbers greater than 200 undergo alpha (α) decay, which results in the emission of a helium-4 nucleus as an alpha (α) particle, \(^4_{2}\alpha\). The general reaction is as follows:
\[\underset{\textrm{parent}}{^A_Z \textrm X}\rightarrow \underset{\textrm{daughter}}{^{A-4}_{Z-2} \textrm X'}+\underset{\textrm{alpha}\\ \textrm{particle}}{^4_2 \alpha}\label{Eq1} \]
The daughter nuclide contains two fewer protons and two fewer neutrons than the parent. Thus α-particle emission produces a daughter nucleus with a mass number A − 4 and a nuclear charge Z − 2 compared to the parent nucleus. Radium-226, for example, undergoes alpha decay to form radon-222:
\[^{226}_{88}\textrm{Ra}\rightarrow ^{222}_{86}\textrm{Rn}+^{4}_{2}\alpha\label{Eq2} \]
Because nucleons are conserved in this and all other nuclear reactions, the sum of the mass numbers of the products, 222 + 4 = 226, equals the mass number of the parent. Similarly, the sum of the atomic numbers of the products, 86 + 2 = 88, equals the atomic number of the parent. Thus the nuclear equation is balanced.
Just as the total number of atoms is conserved in a chemical reaction, the total number of nucleons is conserved in a nuclear reaction.
Beta \(\beta^-\) Decay
Nuclei that contain too many neutrons often undergo beta (β) decay, in which a neutron is converted to a proton and a high-energy electron that is ejected from the nucleus as a β particle:
\[\underset{\textrm{unstable} \\ \textrm{neutron in} \\ \textrm{nucleus}}{^1_0 \textrm n}\rightarrow \underset{\textrm{proton} \\ \textrm{retained} \\ \textrm{by nucleus}}{^{1}_{1} \textrm p}+\underset{\textrm{beta particle} \\ \textrm{emitted by} \\ \textrm{nucleus}}{^0_{-1} \beta}\label{Eq3} \]
The general reaction for beta decay is therefore
\[\underset{\textrm{parent}}{^A_Z \textrm X}\rightarrow \underset{\textrm{daughter}}{^{A}_{Z+1} \textrm X'}+\underset{\textrm{beta particle}}{^0_{-1} \beta}\label{Eq4} \]
Although beta decay does not change the mass number of the nucleus, it does result in an increase of +1 in the atomic number because of the addition of a proton in the daughter nucleus. Thus beta decay decreases the neutron-to-proton ratio, moving the nucleus toward the band of stable nuclei. For example, carbon-14 undergoes beta decay to form nitrogen-14:
\[^{14}_{6}\textrm{C}\rightarrow ^{14}_{7}\textrm{N}+\,^{0}_{-1}\beta \nonumber \]
Once again, the number of nucleons is conserved, and the charges are balanced. The parent and the daughter nuclei have the same mass number, 14, and the sum of the atomic numbers of the products is 6, which is the same as the atomic number of the carbon-14 parent.
Positron \(\beta^+\) Emission
Because a positron has the same mass as an electron but opposite charge, positron emission is the opposite of beta decay. Thus positron emission is characteristic of neutron-poor nuclei, which decay by transforming a proton to a neutron and emitting a high-energy positron:
\[^{1}_{1}\textrm{p}^+\rightarrow ^{1}_{0}\textrm{n}+\,^{0}_{+1}\beta^+\label{Eq6} \]
The general reaction for positron emission is therefore
\[\underset{\textrm{parent}}{^A_Z \textrm X}\rightarrow \underset{\textrm{daughter}}{^{A}_{Z-1} \textrm X'}+\underset{\textrm{positron}}{^0_{+1} \beta^+} \nonumber \]
Like beta decay, positron emission does not change the mass number of the nucleus. In this case, however, the atomic number of the daughter nucleus is lower by 1 than that of the parent. Thus the neutron-to-proton ratio has increased, again moving the nucleus closer to the band of stable nuclei. For example, carbon-11 undergoes positron emission to form boron-11:
\[^{11}_{6}\textrm{C}\rightarrow ^{11}_{5}\textrm{B}+\,^{0}_{+1}\beta^+ \nonumber \]
Nucleons are conserved, and the charges balance. The mass number, 11, does not change, and the sum of the atomic numbers of the products is 6, the same as the atomic number of the parent carbon-11 nuclide.
Electron Capture
A neutron-poor nucleus can decay by either positron emission or electron capture (EC), in which an electron in an inner shell reacts with a proton to produce a neutron:
\[^{1}_{1}\textrm{p} +\; ^{0}_{-1}\textrm{e}\rightarrow \, ^{1}_{0}\textrm n\label{Eq9} \]
When a second electron moves from an outer shell to take the place of the lower-energy electron that was absorbed by the nucleus, an x-ray is emitted. The overall reaction for electron capture is thus
\[\underset{\textrm{parent}}{^A_Z \textrm X}+\underset{\textrm{electron}}{^0_{-1} \textrm e}\rightarrow \underset{\textrm{daughter}}{^{A}_{Z-1} \textrm X'}+\textrm{x-ray} \nonumber \]
Electron capture does not change the mass number of the nucleus because both the proton that is lost and the neutron that is formed have a mass number of 1. As with positron emission, however, the atomic number of the daughter nucleus is lower by 1 than that of the parent. Once again, the neutron-to-proton ratio has increased, moving the nucleus toward the band of stable nuclei. For example, iron-55 decays by electron capture to form manganese-55, which is often written as follows:
\[^{55}_{26}\textrm{Fe}\overset{\textrm{EC}}{\rightarrow}\, ^{55}_{25}\textrm{Mn}+\textrm{x-ray} \nonumber \]
The atomic numbers of the parent and daughter nuclides differ in Equation 20.2.11, although the mass numbers are the same. To write a balanced nuclear equation for this reaction, we must explicitly include the captured electron in the equation:
\[^{55}_{26}\textrm{Fe}+\,^{0}_{-1}\textrm{e}\rightarrow \, ^{55}_{25}\textrm{Mn}+\textrm{x-ray} \nonumber \]
Both positron emission and electron capture are usually observed for nuclides with low neutron-to-proton ratios, but the decay rates for the two processes can be very different.
Gamma \(\gamma\) Emission
Many nuclear decay reactions produce daughter nuclei that are in a nuclear excited state, which is similar to an atom in which an electron has been excited to a higher-energy orbital to give an electronic excited state. Just as an electron in an electronic excited state emits energy in the form of a photon when it returns to the ground state, a nucleus in an excited state releases energy in the form of a photon when it returns to the ground state. These high-energy photons are γ rays. Gamma (\(\gamma\)) emission can occur virtually instantaneously, as it does in the alpha decay of uranium-238 to thorium-234, where the asterisk denotes an excited state:
\[^{238}_{92}\textrm{U}\rightarrow \, \underset{\textrm{excited} \\ \textrm{nuclear} \\ \textrm{state}}{^{234}_{90}\textrm{Th*}} + ^{4}_{2}\alpha\xrightarrow {\textrm{relaxation}\,}\,^{234}_{90}\textrm{Th} + \ce{^0_0\gamma} \nonumber \]
If we disregard the decay event that created the excited nucleus, then
\[^{234}_{88}\textrm{Th*} \rightarrow\, ^{234}_{88}\textrm{Th} + ^{0}_{0}\gamma \nonumber \]
or more generally,
\[^{A}_{Z}\textrm{X*} \rightarrow\, ^{A}_{Z}\textrm{X} + ^{0}_{0}\gamma \nonumber \]
Gamma emission can also occur after a significant delay. For example, technetium-99m has a half-life of about 6 hours before emitting a \(γ\) ray to form technetium-99 (the m is for metastable). Because γ rays are energy, their emission does not affect either the mass number or the atomic number of the daughter nuclide. Gamma-ray emission is therefore the only kind of radiation that does not necessarily involve the conversion of one element to another, although it is almost always observed in conjunction with some other nuclear decay reaction.
Spontaneous Fission
Only very massive nuclei with high neutron-to-proton ratios can undergo spontaneous fission, in which the nucleus breaks into two pieces that have different atomic numbers and atomic masses. This process is most important for the transactinide elements, with Z ≥ 104. Spontaneous fission is invariably accompanied by the release of large amounts of energy, and it is usually accompanied by the emission of several neutrons as well. An example is the spontaneous fission of \(^{254}_{98}\textrm{Cf}\), which gives a distribution of fission products; one possible set of products is shown in the following equation:
\[^{254}_{98}\textrm{Cf}\rightarrow \,^{118}_{46}\textrm{Pd}+\,^{132}_{52}\textrm{Te}+4^{1}_{0}\textrm{n} \nonumber \]
Once again, the number of nucleons is conserved. Thus the sum of the mass numbers of the products (118 + 132 + 4 = 254) equals the mass number of the reactant. Similarly, the sum of the atomic numbers of the products [46 + 52 + (4 × 0) = 98] is the same as the atomic number of the parent nuclide.
Example \(\PageIndex{2}\)
Write a balanced nuclear equation to describe each reaction.
- the beta decay of \(^{35}_{16}\textrm{S}\)
- the decay of \(^{201}_{80}\textrm{Hg}\) by electron capture
- the decay of \(^{30}_{15}\textrm{P}\) by positron emission
Given: radioactive nuclide and mode of decay
Asked for: balanced nuclear equation
Strategy:
A Identify the reactants and the products from the information given.
B Use the values of A and Z to identify any missing components needed to balance the equation.
Solution
a.
A We know the identities of the reactant and one of the products (a β particle). We can therefore begin by writing an equation that shows the reactant and one of the products and indicates the unknown product as \(^{A}_{Z}\textrm{X}\): \[^{35}_{16}\textrm{S}\rightarrow\,^{A}_{Z}\textrm{X}+\,^{0}_{-1}\beta \nonumber \]
B Because both protons and neutrons must be conserved in a nuclear reaction, the unknown product must have a mass number of A = 35 − 0 = 35 and an atomic number of Z = 16 − (−1) = 17. The element with Z = 17 is chlorine, so the balanced nuclear equation is as follows: \[^{35}_{16}\textrm{S}\rightarrow\,^{35}_{17}\textrm{Cl}+\,^{0}_{-1}\beta \nonumber \]
b.A We know the identities of both reactants: \(^{201}_{80}\textrm{Hg}\) and an inner electron, \(^{0}_{-1}\textrm{e}\). The reaction is as follows: \[^{201}_{80}\textrm{Hg}+\,^{0}_{-1}\textrm e\rightarrow\,^{A}_{Z}\textrm{X} \nonumber \]
B Both protons and neutrons are conserved, so the mass number of the product must be A = 201 + 0 = 201, and the atomic number of the product must be Z = 80 + (−1) = 79, which corresponds to the element gold. The balanced nuclear equation is thus \[^{201}_{80}\textrm{Hg}+\,^{0}_{-1}\textrm e\rightarrow\,^{201}_{79}\textrm{Au} \nonumber \]
c.A As in part (a), we are given the identities of the reactant and one of the products—in this case, a positron. The unbalanced nuclear equation is therefore \[^{30}_{15}\textrm{P}\rightarrow\,^{A}_{Z}\textrm{X}+\,^{0}_{+1}\beta \nonumber \]
B The mass number of the second product is A = 30 − 0 = 30, and its atomic number is Z = 15 − 1 = 14, which corresponds to silicon. The balanced nuclear equation for the reaction is as follows: \[^{30}_{15}\textrm{P}\rightarrow\,^{30}_{14}\textrm{Si}+\,^{0}_{+1}\beta \nonumber \]
Exercise \(\PageIndex{2}\)
Write a balanced nuclear equation to describe each reaction.
- \(^{11}_{6}\textrm{C}\) by positron emission
- the beta decay of molybdenum-99
- the emission of an α particle followed by gamma emission from \(^{185}_{74}\textrm{W}\)
- Answer a
-
\(^{11}_{6}\textrm{C}\rightarrow\,^{11}_{5}\textrm{B}+\,^{0}_{+1}\beta\)
- Answer d
-
\(^{99}_{42}\textrm{Mo}\rightarrow\,^{99m}_{43}\textrm{Tc}+\,^{0}_{-1}\beta\)
- Answer c
-
\(^{185}_{74}\textrm{W}\rightarrow\,^{181}_{72}\textrm{Hf}+\,^{4}_{2}\alpha +\,^{0}_{0}\gamma\)
Example \(\PageIndex{3}\)
Predict the kind of nuclear change each unstable nuclide undergoes when it decays.
- \(^{45}_{22}\textrm{Ti}\)
- \(^{242}_{94}\textrm{Pu}\)
- \(^{12}_{5}\textrm{B}\)
- \(^{256}_{100}\textrm{Fm}\)
Given: nuclide
Asked for: type of nuclear decay
Strategy:
Based on the neutron-to-proton ratio and the value of Z, predict the type of nuclear decay reaction that will produce a more stable nuclide.
Solution
- This nuclide has a neutron-to-proton ratio of only 1.05, which is much less than the requirement for stability for an element with an atomic number in this range. Nuclei that have low neutron-to-proton ratios decay by converting a proton to a neutron. The two possibilities are positron emission, which converts a proton to a neutron and a positron, and electron capture, which converts a proton and a core electron to a neutron. In this case, both are observed, with positron emission occurring about 86% of the time and electron capture about 14% of the time.
- Nuclei with Z > 83 are too heavy to be stable and usually undergo alpha decay, which decreases both the mass number and the atomic number. Thus \(^{242}_{94}\textrm{Pu}\) is expected to decay by alpha emission.
- This nuclide has a neutron-to-proton ratio of 1.4, which is very high for a light element. Nuclei with high neutron-to-proton ratios decay by converting a neutron to a proton and an electron. The electron is emitted as a β particle, and the proton remains in the nucleus, causing an increase in the atomic number with no change in the mass number. We therefore predict that \(^{12}_{5}\textrm{B}\) will undergo beta decay.
- This is a massive nuclide, with an atomic number of 100 and a mass number much greater than 200. Nuclides with A ≥ 200 tend to decay by alpha emission, and even heavier nuclei tend to undergo spontaneous fission. We therefore predict that \(^{256}_{100}\textrm{Fm}\) will decay by either or both of these two processes. In fact, it decays by both spontaneous fission and alpha emission, in a 97:3 ratio.
Exercise \(\PageIndex{3}\)
Predict the kind of nuclear change each unstable nuclide undergoes when it decays.
- \(^{32}_{14}\textrm{Si}\)
- \(^{43}_{21}\textrm{Sc}\)
- \(^{231}_{91}\textrm{Pa}\)
- Answer a
-
beta decay
- Answer d
-
positron emission or electron capture
- Answer c
-
alpha decay
Radioactive Decay Series
The nuclei of all elements with atomic numbers greater than 83 are unstable. Thus all isotopes of all elements beyond bismuth in the periodic table are radioactive. Because alpha decay decreases Z by only 2, and positron emission or electron capture decreases Z by only 1, it is impossible for any nuclide with Z > 85 to decay to a stable daughter nuclide in a single step, except via nuclear fission. Consequently, radioactive isotopes with Z > 85 usually decay to a daughter nucleus that is radiaoctive, which in turn decays to a second radioactive daughter nucleus, and so forth, until a stable nucleus finally results. This series of sequential alpha- and beta-decay reactions is called a radioactive decay series. The most common is the uranium-238 decay series, which produces lead-206 in a series of 14 sequential alpha- and beta-decay reactions (Figure \(\PageIndex{2}\)). Although a radioactive decay series can be written for almost any isotope with Z > 85, only two others occur naturally: the decay of uranium-235 to lead-207 (in 11 steps) and thorium-232 to lead-208 (in 10 steps). A fourth series, the decay of neptunium-237 to bismuth-209 in 11 steps, is known to have occurred on the primitive Earth. With a half-life of “only” 2.14 million years, all the neptunium-237 present when Earth was formed decayed long ago, and today all the neptunium on Earth is synthetic.
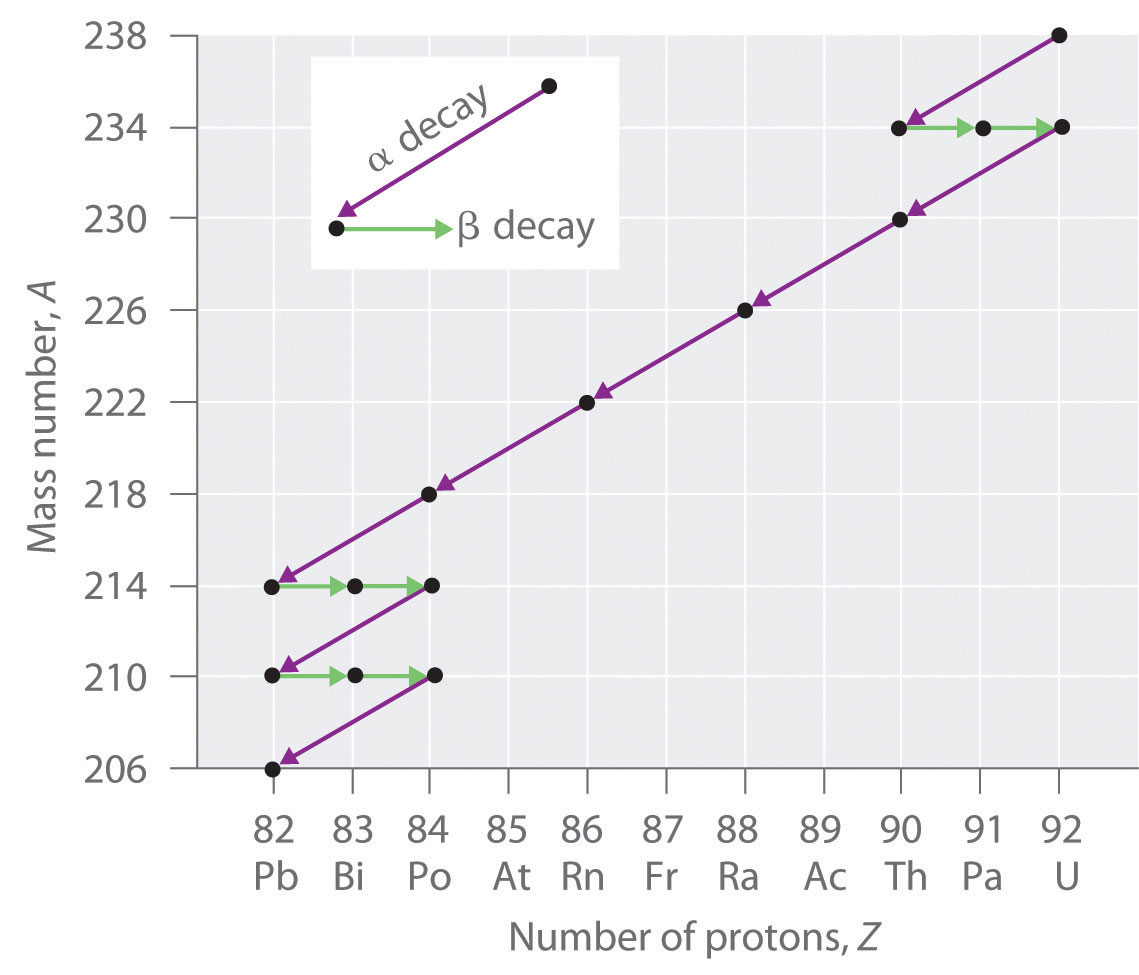
Due to these radioactive decay series, small amounts of very unstable isotopes are found in ores that contain uranium or thorium. These rare, unstable isotopes should have decayed long ago to stable nuclei with a lower atomic number, and they would no longer be found on Earth. Because they are generated continuously by the decay of uranium or thorium, however, their amounts have reached a steady state, in which their rate of formation is equal to their rate of decay. In some cases, the abundance of the daughter isotopes can be used to date a material or identify its origin.
Induced Nuclear Reactions
The discovery of radioactivity in the late 19th century showed that some nuclei spontaneously transform into nuclei with a different number of protons, thereby producing a different element. When scientists realized that these naturally occurring radioactive isotopes decayed by emitting subatomic particles, they realized that—in principle—it should be possible to carry out the reverse reaction, converting a stable nucleus to another more massive nucleus by bombarding it with subatomic particles in a nuclear transmutation reaction.
The first successful nuclear transmutation reaction was carried out in 1919 by Ernest Rutherford, who showed that α particles emitted by radium could react with nitrogen nuclei to form oxygen nuclei. As shown in the following equation, a proton is emitted in the process:
\(^{4}_{2}\alpha + \, ^{14}_{7}\textrm{N} \rightarrow \,^{17}_{8}\textrm{O}+\,^{1}_{1}\textrm{p}\label{Eq17}\)
Rutherford’s nuclear transmutation experiments led to the discovery of the neutron. He found that bombarding the nucleus of a light target element with an α particle usually converted the target nucleus to a product that had an atomic number higher by 1 and a mass number higher by 3 than the target nucleus. Such behavior is consistent with the emission of a proton after reaction with the α particle. Very light targets such as Li, Be, and B reacted differently, however, emitting a new kind of highly penetrating radiation rather than a proton. Because neither a magnetic field nor an electrical field could deflect these high-energy particles, Rutherford concluded that they were electrically neutral. Other observations suggested that the mass of the neutral particle was similar to the mass of the proton. In 1932, James Chadwick (Nobel Prize in Physics, 1935), who was a student of Rutherford’s at the time, named these neutral particles neutrons and proposed that they were fundamental building blocks of the atom. The reaction that Chadwick initially used to explain the production of neutrons was as follows:
\[^{4}_{2}\alpha + \, ^{9}_{4}\textrm{Be} \rightarrow \,^{12}_{6}\textrm{C}+\,^{1}_{0}\textrm{n}\label{Eq18} \]
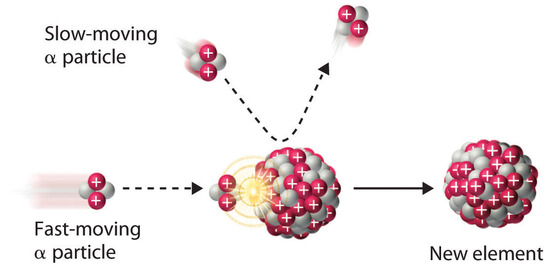
Because α particles and atomic nuclei are both positively charged, electrostatic forces cause them to repel each other. Only α particles with very high kinetic energy can overcome this repulsion and collide with a nucleus (Figure \(\PageIndex{3}\)). Neutrons have no electrical charge, however, so they are not repelled by the nucleus. Hence bombardment with neutrons is a much easier way to prepare new isotopes of the lighter elements. In fact, carbon-14 is formed naturally in the atmosphere by bombarding nitrogen-14 with neutrons generated by cosmic rays:
\[^{1}_{0}\textrm{n} + \, ^{14}_{7}\textrm{N} \rightarrow \,^{14}_{6}\textrm{C}+\,^{1}_{1}\textrm{p}\label{Eq19} \]
Example \(\PageIndex{4}\)
In 1933, Frédéric Joliot and Iréne Joliot-Curie (daughter of Marie and Pierre Curie) prepared the first artificial radioactive isotope by bombarding aluminum-27 with α particles. For each 27Al that reacted, one neutron was released. Identify the product nuclide and write a balanced nuclear equation for this transmutation reaction.
Given: reactants in a nuclear transmutation reaction
Asked for: product nuclide and balanced nuclear equation
Strategy:
A Based on the reactants and one product, identify the other product of the reaction. Use conservation of mass and charge to determine the values of Z and A of the product nuclide and thus its identity.
B Write the balanced nuclear equation for the reaction.
Solution
A Bombarding an element with α particles usually produces an element with an atomic number that is 2 greater than the atomic number of the target nucleus. Thus we expect that aluminum (Z = 13) will be converted to phosphorus (Z = 15). With one neutron released, conservation of mass requires that the mass number of the other product be 3 greater than the mass number of the target. In this case, the mass number of the target is 27, so the mass number of the product will be 30. The second product is therefore phosphorus-30, \(^{30}_{15}\textrm{P}\).
B The balanced nuclear equation for the reaction is as follows:
\[^{27}_{13}\textrm{Al} + \, ^{4}_{2}\alpha \rightarrow \,^{30}_{15}\textrm{P}+\,^{1}_{0}\textrm{n} \nonumber \]
Exercise \(\PageIndex{4}\)
Because all isotopes of technetium are radioactive and have short half-lives, it does not exist in nature. Technetium can, however, be prepared by nuclear transmutation reactions. For example, bombarding a molybdenum-96 target with deuterium nuclei \((^{2}_{1}\textrm{H})\) produces technetium-97. Identify the other product of the reaction and write a balanced nuclear equation for this transmutation reaction.
- Answer
-
neutron, \(^{1}_{0}\textrm{n}\) ; \(^{96}_{42}\textrm{Mo} + \, ^{2}_{1}\textrm{H} \rightarrow \,^{97}_{43}\textrm{Tc}+\,^{1}_{0}\textrm{n}\) :
We noted earlier in this section that very heavy nuclides, corresponding to Z ≥ 104, tend to decay by spontaneous fission. Nuclides with slightly lower values of Z, such as the isotopes of uranium (Z = 92) and plutonium (Z = 94), do not undergo spontaneous fission at any significant rate. Some isotopes of these elements, however, such as \(^{235}_{92}\textrm{U}\) and \(^{239}_{94}\textrm{Pu}\) undergo induced nuclear fission when they are bombarded with relatively low-energy neutrons, as shown in the following equation for uranium-235 and in Figure \(\PageIndex{4}\):
\[^{235}_{92}\textrm{U} + \, ^{1}_{0}\textrm{n} \rightarrow \,^{236}_{92}\textrm{U}\rightarrow \,^{141}_{56}\textrm{Ba}+\,^{92}_{36}\textrm{Kr}+3^{1}_{0}\textrm{n}\label{Eq20} \]
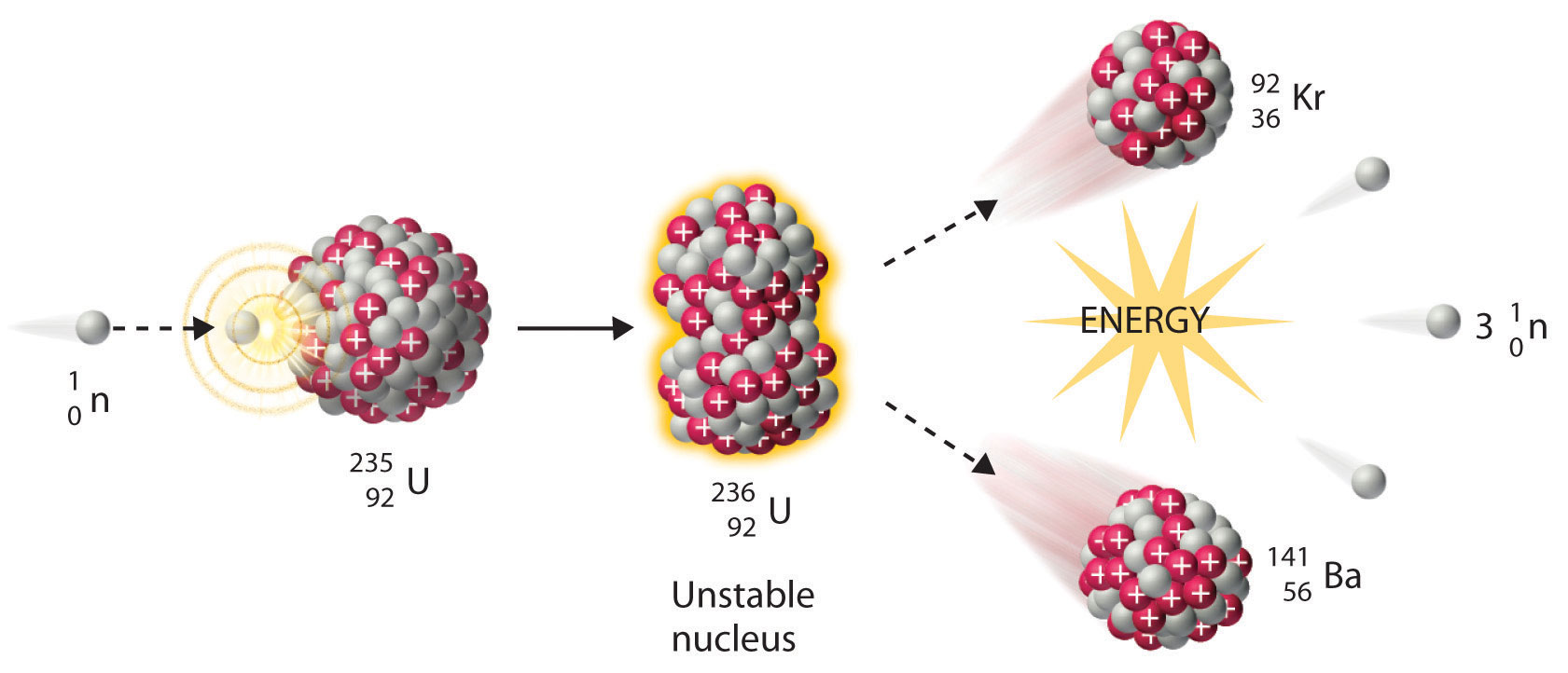
Any isotope that can undergo a nuclear fission reaction when bombarded with neutrons is called a fissile isotope.
During nuclear fission, the nucleus usually divides asymmetrically rather than into two equal parts, as shown in Figure \(\PageIndex{4}\). Moreover, every fission event of a given nuclide does not give the same products; more than 50 different fission modes have been identified for uranium-235, for example. Consequently, nuclear fission of a fissile nuclide can never be described by a single equation. Instead, as shown in Figure \(\PageIndex{5}\), a distribution of many pairs of fission products with different yields is obtained, but the mass ratio of each pair of fission products produced by a single fission event is always roughly 3:2.
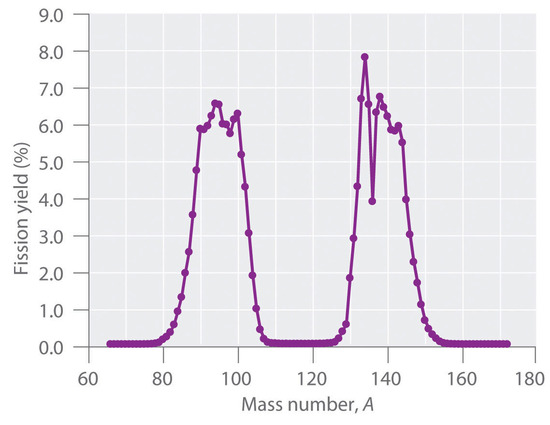
Synthesis of Transuranium Elements
Uranium (Z = 92) is the heaviest naturally occurring element. Consequently, all the elements with Z > 92, the transuranium elements, are artificial and have been prepared by bombarding suitable target nuclei with smaller particles. The first of the transuranium elements to be prepared was neptunium (Z = 93), which was synthesized in 1940 by bombarding a 238U target with neutrons. As shown in Equation 20.21, this reaction occurs in two steps. Initially, a neutron combines with a 238U nucleus to form 239U, which is unstable and undergoes beta decay to produce 239Np:
\(^{238}_{92}\textrm{U} + \, ^{1}_{0}\textrm{n} \rightarrow \,^{239}_{92}\textrm{U}\rightarrow \,^{239}_{93}\textrm{Np}+\,^{0}_{-1}\beta\label{Eq21}\)
Subsequent beta decay of 239Np produces the second transuranium element, plutonium (Z = 94):
\(^{239}_{93}\textrm{Np} \rightarrow \,^{239}_{94}\textrm{Pu}+\,^{0}_{-1}\beta\label{Eq22}\)
Bombarding the target with more massive nuclei creates elements that have atomic numbers significantly greater than that of the target nucleus (Table \(\PageIndex{2}\)). Such techniques have resulted in the creation of the superheavy elements 114 and 116, both of which lie in or near the “island of stability."
| \(^{239}_{94}\textrm{Pu}+\,^{4}_{2}\alpha \rightarrow \,^{242}_{96}\textrm{Cm}+\,^{1}_{0}\textrm{n}\) |
|---|
| \(^{239}_{94}\textrm{Pu}+\,^{4}_{2}\alpha \rightarrow \,^{241}_{95}\textrm{Am}+\,^{1}_{1}\textrm{p}+\,^{1}_{0}\textrm{n}\) |
| \(^{242}_{96}\textrm{Cm}+\,^{4}_{2}\alpha \rightarrow \,^{243}_{97}\textrm{Bk}+\,^{1}_{1}\textrm{p}+2^{1}_{0}\textrm{n}\) |
| \(^{253}_{99}\textrm{Es}+\,^{4}_{2}\alpha \rightarrow \,^{256}_{101}\textrm{Md}+\,^{1}_{0}\textrm{n}\) |
| \(^{238}_{92}\textrm{U}+\,^{12}_{6}\textrm{C} \rightarrow \,^{246}_{98}\textrm{Cf}+4^{1}_{0}\textrm{n}\) |
| \(^{252}_{98}\textrm{Cf}+\,^{10}_{5}\textrm{B} \rightarrow \,^{256}_{103}\textrm{Lr}+6^{1}_{0}\textrm{n}\) |
A device called a particle accelerator is used to accelerate positively charged particles to the speeds needed to overcome the electrostatic repulsions between them and the target nuclei by using electrical and magnetic fields. Operationally, the simplest particle accelerator is the linear accelerator (Figure \(\PageIndex{6}\)), in which a beam of particles is injected at one end of a long evacuated tube. Rapid alternation of the polarity of the electrodes along the tube causes the particles to be alternately accelerated toward a region of opposite charge and repelled by a region with the same charge, resulting in a tremendous acceleration as the particle travels down the tube. A modern linear accelerator such as the Stanford Linear Accelerator (SLAC) at Stanford University is about 2 miles long.
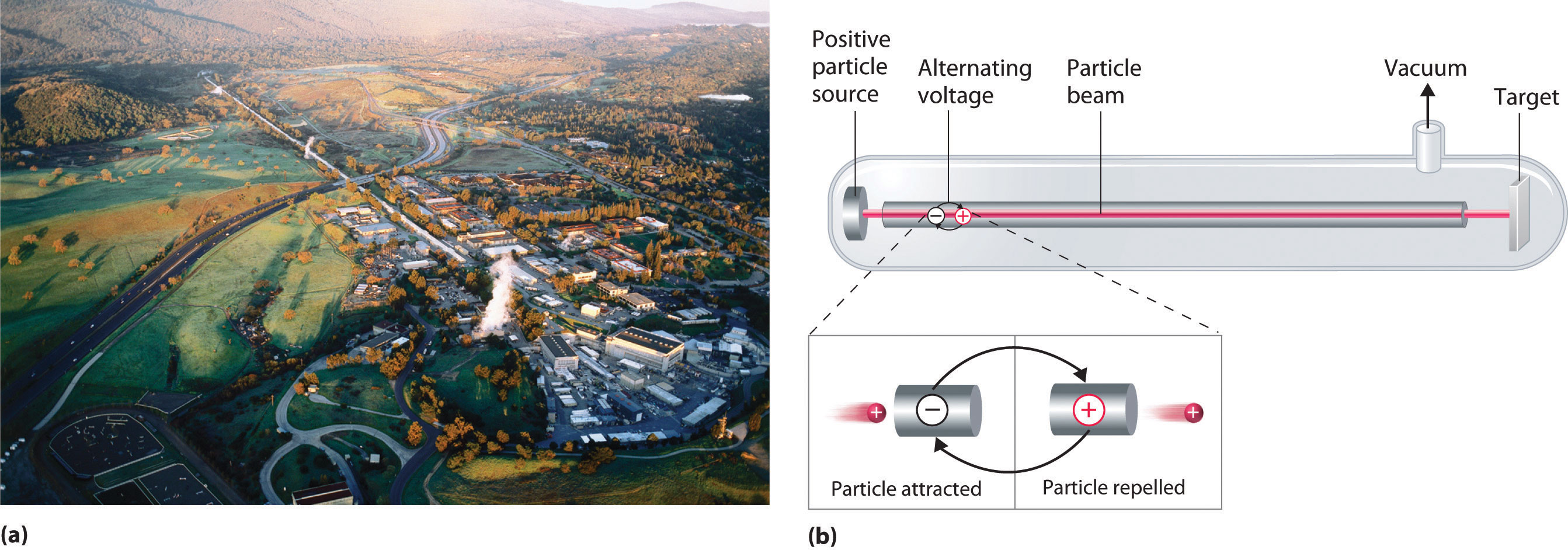
To achieve the same outcome in less space, a particle accelerator called a cyclotron forces the charged particles to travel in a circular path rather than a linear one. The particles are injected into the center of a ring and accelerated by rapidly alternating the polarity of two large D-shaped electrodes above and below the ring, which accelerates the particles outward along a spiral path toward the target.
The length of a linear accelerator and the size of the D-shaped electrodes in a cyclotron severely limit the kinetic energy that particles can attain in these devices. These limitations can be overcome by using a synchrotron, a hybrid of the two designs. A synchrotron contains an evacuated tube similar to that of a linear accelerator, but the tube is circular and can be more than a mile in diameter. Charged particles are accelerated around the circle by a series of magnets whose polarities rapidly alternate.
Summary and Key Takeaway
- Nuclear decay reactions occur spontaneously under all conditions and produce more stable daughter nuclei, whereas nuclear transmutation reactions are induced and form a product nucleus that is more massive than the starting material.
In nuclear decay reactions (or radioactive decay), the parent nucleus is converted to a more stable daughter nucleus. Nuclei with too many neutrons decay by converting a neutron to a proton, whereas nuclei with too few neutrons decay by converting a proton to a neutron. Very heavy nuclei (with A ≥ 200 and Z > 83) are unstable and tend to decay by emitting an α particle. When an unstable nuclide undergoes radioactive decay, the total number of nucleons is conserved, as is the total positive charge. Six different kinds of nuclear decay reactions are known. Alpha decay results in the emission of an α particle, \(^4 _2 \alpha\), and produces a daughter nucleus with a mass number that is lower by 4 and an atomic number that is lower by 2 than the parent nucleus. Beta decay converts a neutron to a proton and emits a high-energy electron, producing a daughter nucleus with the same mass number as the parent and an atomic number that is higher by 1. Positron emission is the opposite of beta decay and converts a proton to a neutron plus a positron. Positron emission does not change the mass number of the nucleus, but the atomic number of the daughter nucleus is lower by 1 than the parent. In electron capture (EC), an electron in an inner shell reacts with a proton to produce a neutron, with emission of an x-ray. The mass number does not change, but the atomic number of the daughter is lower by 1 than the parent. In gamma emission, a daughter nucleus in a nuclear excited state undergoes a transition to a lower-energy state by emitting a γ ray. Very heavy nuclei with high neutron-to-proton ratios can undergo spontaneous fission, in which the nucleus breaks into two pieces that can have different atomic numbers and atomic masses with the release of neutrons. Many very heavy nuclei decay via a radioactive decay series—a succession of some combination of alpha- and beta-decay reactions. In nuclear transmutation reactions, a target nucleus is bombarded with energetic subatomic particles to give a product nucleus that is more massive than the original. All transuranium elements—elements with Z > 92—are artificial and must be prepared by nuclear transmutation reactions. These reactions are carried out in particle accelerators such as linear accelerators, cyclotrons, and synchrotrons.
Key Equations
alpha decay
\[^A_Z \textrm X\rightarrow \, ^{A-4}_{Z-2} \textrm X'+\,^4_2 \alpha \nonumber \]
beta decay
\[^A_Z \textrm X\rightarrow \, ^{A}_{Z+1} \textrm X'+\,^0_{-1} \beta \nonumber \]
positron emission
\[^A_Z \textrm X\rightarrow \, ^{A}_{Z-1} \textrm X'+\,^0_{+1} \beta \nonumber \]
electron capture
\[^A_Z \textrm X+\,^{0}_{-1} \textrm e\rightarrow \, ^{A}_{Z-1} \textrm X'+\textrm{x-ray} \nonumber \]
gamma emission
\[^A_Z \textrm{X*}\rightarrow \, ^{A}_{Z} \textrm X+\,^0_{0} \gamma \nonumber \]

