5.7: Collision Theory
- Page ID
- 82048
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Molecules must collide in order to react.
- In order to effectively initiate a reaction, collisions must be sufficiently energetic (kinetic energy) to break chemical bonds; this energy is known as the activation energy.
- As the temperature rises, molecules move faster and collide more vigorously, greatly increasing the likelihood of bond breakage upon collision.
Collision theory explains why different reactions occur at different rates, and suggests ways to change the rate of a reaction. Collision theory states that for a chemical reaction to occur, the reacting particles must collide with one another. The rate of the reaction depends on the frequency of collisions. The theory also tells us that reacting particles often collide without reacting. For collisions to be successful, reacting particles must (1) collide with (2) sufficient energy, and (3) with the proper orientation.
Requirement 1: Molecules Must Collide to React
Collision Theory provides a qualitative explanation of chemical reactions and the rates at which they occur. A basic principal of collision theory is that, in order to react, molecules must collide. This fundamental rule guides any analysis of an ordinary reaction mechanism. Consider a simple bimolecular step:
\[A + B \rightarrow Products\]
If the two molecules \(A\) and \(B\) are to react, they must approach closely enough to disrupt some of their existing bonds and to permit the creation of any new ones that are needed in the products. Such an encounter is called a collision. The frequency of collisions between \(A\) and \(B\) in a gas is proportional to the concentration of each; if [A] is doubled, the frequency of \(A-B\) collisions will double, and doubling \([B]\) will have the same effect. If all collisions lead to products, then the rate of a bimolecular process is first-order in A and in B, or second-order overall:
\[rate = k[A][B]\]
The need for collisions fundamental to any analysis of an ordinary reaction mechanism and explains why termolecular processes (three species colliding and reaction) are so uncommon. The kinetic theory of gases states that for every 1000 binary collisions, there will be only one event in which three molecules simultaneously come together. Four-way collisions are so improbable that this process has never been demonstrated in an elementary reaction.
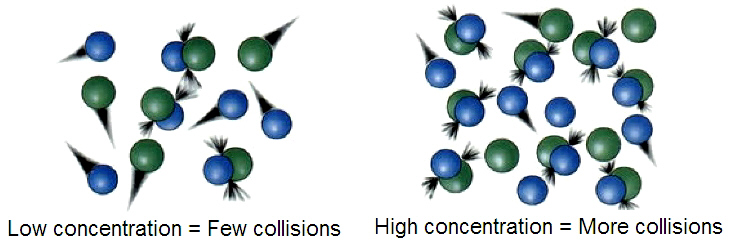
The frequency of collisions between A and B in a gas is proportional to the concentration of each.
Consider the reaction in the Haber process for making ammonia:
\[\ce{N_2 (g) + 3 H_2 (g) } \rightleftharpoons \ce{2NH_3} (g) \label{eq3}\]
the collision theory says that \(\ce{H_2}\) and \(\ce{N_2}\) will only react when they collide. Hence, the more frequently they collide, the faster the rate of reaction. This can be achieved easily by either increasing the pressure on the gasses to bring \(\ce{H_2}\) and \(\ce{N_2}\) closer together on average or by increasing the temperature to makes molecules move faster.
Car damage can be very expensive, especially if the person hitting your car does not have insurance. Many people have had the experience of backing up while parallel parking and hearing that "bump". Fortunately, there is often no damage because the cars were not going fast enough. But every once in a while there is a rearrangement of the body parts of a car when it is hit with sufficient speed. Then things need to be fixed - this akin to a reaction, albeit on a macroscopic scale.

Requirement 2: Not all Collisions are Sufficiently Energetic
In the Haber process (Equation \(\ref{eq3}\)) at 300 K only 1 in \(10^{11}\) collisions between \(H_2\) and \(N_2\) results in a reaction! At 800 K, this increases to 1 in \(10^4\) collisions resulting in a reaction. Hence, while the collisions are needed for a reaction, other aspects contribute. Reacting particles can form products when they collide with one another provided those collisions have enough kinetic energy and the correct orientation. Particles that lack the necessary kinetic energy may collide, but the particles will simply bounce off one another unchanged. Figure \(\PageIndex{1}\) illustrates the difference. In the first collision, the particles bounce off one another and no rearrangement of atoms has occurred. The second collision occurs with greater kinetic energy, and so the bond between the two red atoms breaks. One red atom bonds with the other molecule as one product, while the single red atom is the other product. The first collision is called an ineffective collision, while the second collision is called an effective collision.
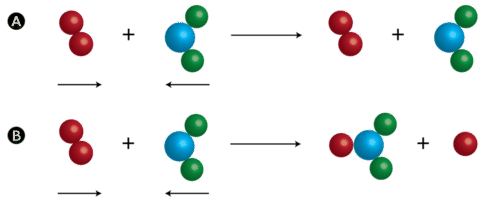
For a gas at room temperature and normal atmospheric pressure, there are about 1033 collisions in each cubic centimeter of space every second. If every collision between two reactant molecules yielded products, all reactions would be complete in a fraction of a second. For example, when two billiard balls collide, they simply bounce off of each other. This is the most likely outcome if the reaction between A and B requires a significant disruption or rearrangement of the bonds between their atoms. In order to effectively initiate a reaction, collisions must be sufficiently energetic (or have sufficient kinetic energy) to bring about this bond disruption.
A reaction will not take place unless the particles collide with a certain minimum energy called the activation energy of the reaction. Activation energy is the minimum energy required to make a reaction occur. This can be illustrated on an energy profile for the reaction. An energy profile for a simple exothermic reaction is given in the Figure \(\PageIndex{2}\).
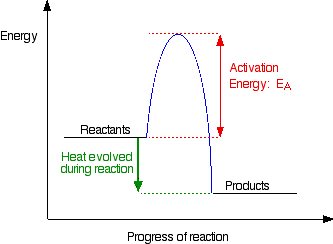
If the particles collide with less energy than the activation energy, nothing interesting happens. They bounce apart. The activation energy can be thought of as a barrier to the reaction. Only those collisions with energies equal to or greater than the activation energy result in a reaction.
Any chemical reaction results in the breaking of some bonds (which requires energy) and the formation of new ones (which releases energy). Some bonds must be broken before new ones can be formed. Activation energy is involved in breaking some of the original bonds. If a collision is relatively gentle, there is insufficient energy available to initiate the bond-breaking process, and thus the particles do not react.
Energetic collisions between molecules cause interatomic bonds to stretch and bend, temporarily weakening them so that they become more susceptible to cleavage. Distortion of the bonds can expose their associated electron clouds to interactions with other reactants that might lead to the formation of new bonds.
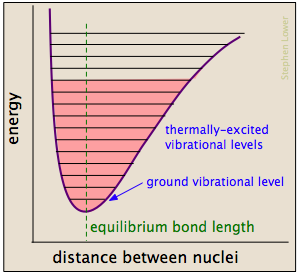
Chemical bonds have some of the properties of mechanical springs: their potential energies depend on the extent to which they are stretched or compressed. Each atom-to-atom bond can be described by a potential energy diagram that shows how its energy changes with its length. When the bond absorbs energy (either from heating or through a collision), it is elevated to a higher quantized vibrational state (indicated by the horizontal lines) that weakens the bond as its length oscillates between the extended limits corresponding to the curve in Figure \(\PageIndex{3}\).
When the bond absorbs energy (either from heating or through a collision), it is elevated to a higher quantized vibrational state (indicated by the horizontal lines) that weakens the bond.
A particular collision will typically excite a number of bonds in this way. Within about 10–13 seconds, this excitation is distributed among the other bonds in the molecule in complex and unpredictable ways that can concentrate the added energy at a particularly vulnerable point. The affected bond can stretch and bend farther, making it more susceptible to cleavage. Even if the bond does not break by pure stretching, it can become distorted or twisted so as to expose nearby electron clouds to interactions with other reactants that might encourage a reaction.
Example \(\PageIndex{1}\)
- Draw a simple energy profile for an exothermic reaction in which 100 kJ mol-1 is evolved, and which has an activation energy of 50 kJ mol-1 .
- Draw a simple energy profile for an endothermic reaction in which 50 kJ mol-1 is absorbed and which has an activation energy of 100 kJ mol-1
- Explain why all reactions have an activation energy, using your knowledge of collision theory.
- Answer
-
c: All reactions have an activation energy because energy is required to make the reactants combine in a way that will cause the reaction. No chemical process can take place without having at least a little energy to get things started.
Exercise \(\PageIndex{1}\)
To increase the rate of a reaction, there must be (select one):
- Decrease in the frequency of collisions
- An Increase in the frequency of collisions.
- A decrease in the frequency of effective collisions
- An increase in the frequency of effective collisions
- Answer
-
D
The Maxwell-Boltzmann Distribution
Because of the key role of activation energy in deciding whether a collision will result in a reaction, it is useful to know the proportion of the particles present with high enough energies to react when they collide. In any system, the particles present will have a very wide range of energies. For gases, this can be shown on a graph called the Maxwell-Boltzmann distribution, a plot showing the number of particles with each particular energy.
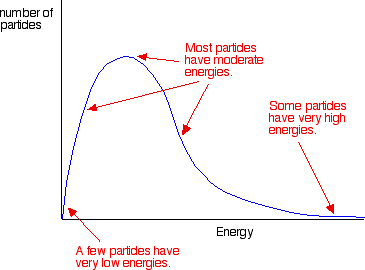
The area under the curve measures of the total number of particles present. Remember that for a reaction to occur, particles must collide with energies equal to or greater than the activation energy for the reaction. The activation energy is marked on the Maxwell-Boltzmann distribution with a green line:
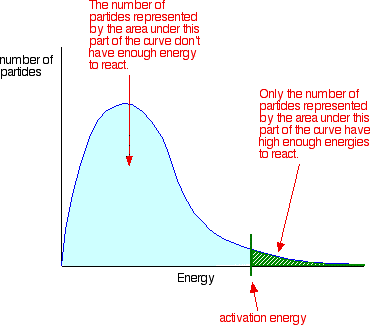
Notice that the large majority of the particles have insufficient energy to react when they collide. To enable them to react, either the shape of the curve must be altered, or the activation energy shifted further to the left to lower energies.
Requirement 3: Not all Collisions are Sufficiently Oriented
Even if two molecules collide with sufficient activation energy, there is no guarantee that the collision will be successful. In fact, the collision theory says that not every collision is successful, even if molecules are moving with enough energy. The reason for this is because molecules also need to collide with the right orientation, so that the proper atoms line up with one another, and bonds can break and re-form in the necessary fashion. However, because molecules in the liquid and gas phase are in constant, random motion, there is always the probability that two molecules will collide in just the right way for them to react.
Consider a simple reaction involving a collision between two molecules: for example, ethene, \(\ce{CH_2=CH_2}\), and hydrogen chloride, \(HCl\). These react to give chloroethane as shown:
\[\ce{ H_2C=CH_2 + HCl \rightarrow CH_3CH_2Cl}\]
As a result of the collision between the two molecules, the double bond in ethene is converted into a single bond. A hydrogen atom is now attached to one of the carbons and a chlorine atom to the other. The reaction can only happen if the hydrogen end of the H-Cl bond approaches the carbon-carbon double bond. No other collision between the two molecules produces the same effect. The two simply bounce off each other.

With no knowledge of the reaction mechanism, one might wonder why collision 2 would be unsuccessful. The double bond has a high concentration of negative charge around it due to the electrons in the bonds. The approaching chlorine atom is also partially negative due to dipole created by the electronegativity difference between it and hydrogen. The repulsion simply causes the molecules to bounce off each other. In any collision involving unsymmetrical species, the way they hit each other is important in determining whether a reaction occurs.
Unimolecular processes also begin with a Collision
Until about 1921, chemists did not understand the role of collisions in unimolecular processes. It turns out that the mechanisms of such reactions are actually quite complicated, and that at very low pressures they do follow second-order kinetics. Such reactions are more properly described as pseudounimolecular. The cyclopropane isomerization described in Example 1 is typical of many decomposition reactions found to follow first-order kinetics, implying that the process is unimolecular.
Consider, for example, the isomerization of cyclopropane to propene, which takes place at fairly high temperatures in the gas phase:

The collision-to-product sequence can be conceptualized in the following [grossly oversimplified] way:
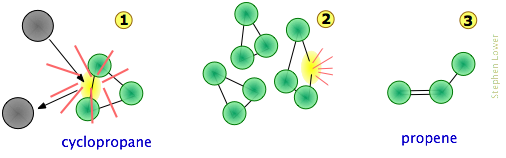
Note that
- For simplicity, the hydrogen atoms are not shown here. This is reasonable because C–C bonds are weaker then C–H bonds, which are less likely to be affected.
- The collision at 1 is most likely with another cyclopropane molecule, but because no part of the colliding molecule gets incorporated into the product, it can in principle be a noble gas or some other non-reacting species;
- Although the C–C bonds in cyclopropane are all identical, the instantaneous localization of the collisional energy can distort the molecule in various ways (2), leading to a configuration sufficiently unstable to initiate the rearrangement to the product.
Of course, the more critical this orientational requirement is, like it is for larger or more complex molecules, the fewer collisions there will be that will be effective. An effective collision is defined as one in which molecules collide with sufficient energy and proper orientation, so that a reaction occurs.
Exercise \(\PageIndex{2}\)
According to collision theory, what three criteria are needed to be met before a bimolecular reaction can take place?
- The orientation probability factor must be 1.
- The collision energy must be greater than the activation energy for the reaction.
- The collision must occur in the proper orientation.
- The collision frequency must be greater than the frequency factor for the reaction.
- A collision between the reactants must occur.
Exercise \(\PageIndex{3}\)
How will the given change affect the rate of an elementary reaction.
- An increase in temperature.
- An increase in the activation energy for the reaction
- An increase in the reactant concentration.
- An increase in the size of one of the reactants in a bimolecular reaction
Summary
Collision Theory provides a qualitative explanation of chemical reactions and the rates at which they occur. For a chemical reaction to occur, an energy threshold must be overcome, and the reacting species must also have the correct spatial orientation. Factors that increase the rate of a reaction must influence at least one of the following:
- How often collisions occur - more frequent collisions will mean a faster rate.
- More effective collisions in terms of collisions occurring with sufficient energy
- More effective collisions in terms of collisions occurring with the proper orientation.
Two more topics must be examined before these can be discussed in depth: reaction mechanisms and the concept of threshold energy.
Contributors and Attributions
- Peggy Lawson (Oxbow Prairie Heights School)
Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook

