13.8: Freezing-Point Depression and Boiling-Point Elevation of Nonelectrolyte Solutions
- Page ID
- 42239
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To describe the relationship between solute concentration and the physical properties of a solution.
- To understand that the total number of nonvolatile solute particles determines the decrease in vapor pressure, increase in boiling point, and decrease in freezing point of a solution versus the pure solvent.
Many of the physical properties of solutions differ significantly from those of the pure substances discussed in earlier chapters, and these differences have important consequences. For example, the limited temperature range of liquid water (0°C–100°C) severely limits its use. Aqueous solutions have both a lower freezing point and a higher boiling point than pure water. Probably one of the most familiar applications of this phenomenon is the addition of ethylene glycol (“antifreeze”) to the water in an automobile radiator. This solute lowers the freezing point of the water, preventing the engine from cracking in very cold weather from the expansion of pure water on freezing. Antifreeze also enables the cooling system to operate at temperatures greater than 100°C without generating enough pressure to explode.
Changes in the freezing point and boiling point of a solution depend primarily on the number of solute particles present rather than the kind of particles. Such properties of solutions are called colligative properties (from the Latin colligatus, meaning “bound together” as in a quantity). As we will see, the vapor pressure and osmotic pressure of solutions are also colligative properties.
When we determine the number of particles in a solution, it is important to remember that not all solutions with the same molarity contain the same concentration of solute particles. Consider, for example, 0.01 M aqueous solutions of sucrose, \(NaCl\), and \(\ce{CaCl_2}\). Because sucrose dissolves to give a solution of neutral molecules, the concentration of solute particles in a 0.01 M sucrose solution is 0.01 M. In contrast, both \(\ce{NaCl}\) and \(\ce{CaCl_2}\) are ionic compounds that dissociate in water to yield solvated ions. As a result, a 0.01 M aqueous solution of \(\ce{NaCl}\) contains 0.01 M Na+ ions and 0.01 M \(Cl^−\) ions, for a total particle concentration of 0.02 M. Similarly, the \(\ce{CaCl_2}\) solution contains 0.01 M \(Ca^{2+}\) ions and 0.02 M \(Cl^−\) ions, for a total particle concentration of 0.03 M.These values are correct for dilute solutions, where the dissociation of the compounds to form separately solvated ions is complete. At higher concentrations (typically >1 M), especially with salts of small, highly charged ions (such as \(Mg^{2+}\) or \(Al^{3+}\)), or in solutions with less polar solvents, dissociation to give separate ions is often incomplete. The sum of the concentrations of the dissolved solute particles dictates the physical properties of a solution. In the following discussion, we must therefore keep the chemical nature of the solute firmly in mind.
Boiling Point Elevation
Recall that the normal boiling point of a substance is the temperature at which the vapor pressure equals 1 atm. If a nonvolatile solute lowers the vapor pressure of a solvent, it must also affect the boiling point. Because the vapor pressure of the solution at a given temperature is less than the vapor pressure of the pure solvent, achieving a vapor pressure of 1 atm for the solution requires a higher temperature than the normal boiling point of the solvent. Thus the boiling point of a solution is always greater than that of the pure solvent. We can see why this must be true by comparing the phase diagram for an aqueous solution with the phase diagram for pure water (Figure \(\PageIndex{1}\)). The vapor pressure of the solution is less than that of pure water at all temperatures. Consequently, the liquid–vapor curve for the solution crosses the horizontal line corresponding to P = 1 atm at a higher temperature than does the curve for pure water.
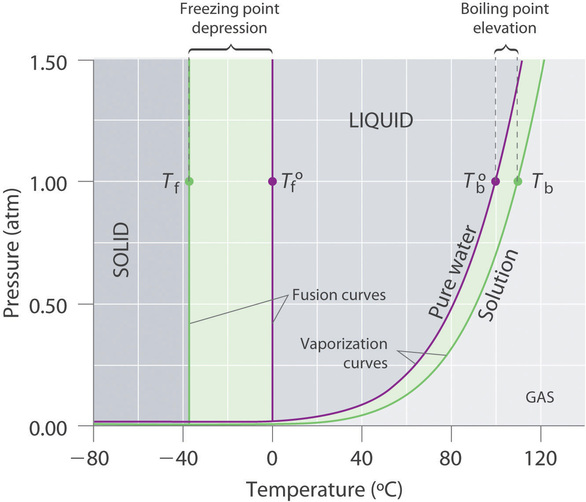
The boiling point of a solution with a nonvolatile solute is always greater than the boiling point of the pure solvent.
The magnitude of the increase in the boiling point is related to the magnitude of the decrease in the vapor pressure. As we have just discussed, the decrease in the vapor pressure is proportional to the concentration of the solute in the solution. Hence the magnitude of the increase in the boiling point must also be proportional to the concentration of the solute (Figure \(\PageIndex{2}\)). We can define the boiling point elevation (\(ΔT_b\)) as the difference between the boiling points of the solution and the pure solvent:
\[ΔT_b=T_b−T^0_b \label{eq1}\]
where \(T_b\) is the boiling point of the solution and \(T^0_b\) is the boiling point of the pure solvent. We can express the relationship between \(ΔT_b\) and concentration as follows
\[ΔT_b = mK_b \label{eq2}\]
where m is the concentration of the solute expressed in molality, and \(K_b\) is the molal boiling point elevation constant of the solvent, which has units of °C/m. Table \(\PageIndex{1}\) lists characteristic Kb values for several commonly used solvents.
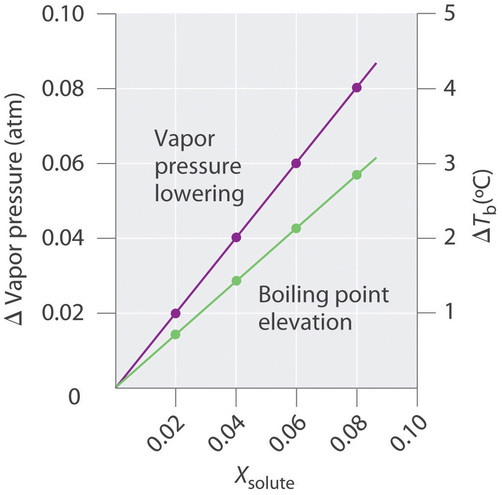
For relatively dilute solutions, the magnitude of both properties is proportional to the solute concentration.
| Solvent | Boiling Point (°C) | Kb (°C/m) | Freezing Point (°C) | Kf (°C/m) |
|---|---|---|---|---|
| acetic acid | 117.90 | 3.22 | 16.64 | 3.63 |
| benzene | 80.09 | 2.64 | 5.49 | 5.07 |
| d-(+)-camphor | 207.4 | 4.91 | 178.8 | 37.8 |
| carbon disulfide | 46.2 | 2.42 | −112.1 | 3.74 |
| carbon tetrachloride | 76.8 | 5.26 | −22.62 | 31.4 |
| chloroform | 61.17 | 3.80 | −63.41 | 4.60 |
| nitrobenzene | 210.8 | 5.24 | 5.70 | 6.87 |
| water | 100.00 | 0.51 | 0.00 | 1.86 |
The concentration of the solute is typically expressed as molality rather than mole fraction or molarity for two reasons. First, because the density of a solution changes with temperature, the value of molarity also varies with temperature. If the boiling point depends on the solute concentration, then by definition the system is not maintained at a constant temperature. Second, molality and mole fraction are proportional for relatively dilute solutions, but molality has a larger numerical value (a mole fraction can be only between zero and one). Using molality allows us to eliminate nonsignificant zeros.
According to Table \(\PageIndex{1}\), the molal boiling point elevation constant for water is 0.51°C/m. Thus a 1.00 m aqueous solution of a nonvolatile molecular solute such as glucose or sucrose will have an increase in boiling point of 0.51°C, to give a boiling point of 100.51°C at 1.00 atm. The increase in the boiling point of a 1.00 m aqueous \(\ce{NaCl}\) solution will be approximately twice as large as that of the glucose or sucrose solution because 1 mol of \(\ce{NaCl}\) produces 2 mol of dissolved ions. Hence a 1.00 m \(\ce{NaCl}\) solution will have a boiling point of about 101.02°C.
In Example \(\PageIndex{1}\), we calculated that the vapor pressure of a 30.2% aqueous solution of ethylene glycol at 100°C is 85.1 mmHg less than the vapor pressure of pure water. We stated (without offering proof) that this should result in a higher boiling point for the solution compared with pure water. Now that we have seen why this assertion is correct, calculate the boiling point of the aqueous ethylene glycol solution.
Given: composition of solution
Asked for: boiling point
Strategy:
Calculate the molality of ethylene glycol in the 30.2% solution. Then use Equation \ref{eq2} to calculate the increase in boiling point.
Solution:
From Example \(\PageIndex{1}\), we know that a 30.2% solution of ethylene glycol in water contains 302 g of ethylene glycol (4.87 mol) per 698 g of water. The molality of the solution is thus
\[\text{molality of ethylene glycol}= \left(\dfrac{4.87 \;mol}{698 \; \cancel{g} \;H_2O} \right) \left(\dfrac{1000\; \cancel{g}}{1 \;kg} \right)=6.98 m\]
From Equation \ref{eq2}, the increase in boiling point is therefore
\[ΔT_b=mK_b=(6.98 \cancel{m})(0.51°C/\cancel{m})=3.6°C\]
The boiling point of the solution is thus predicted to be 104°C. With a solute concentration of almost 7 m, however, the assumption of a dilute solution used to obtain Equation \ref{eq2} may not be valid.
Assume that a tablespoon (5.00 g) of \(\ce{NaCl}\) is added to 2.00 L of water at 20.0°C, which is then brought to a boil to cook spaghetti. At what temperature will the water boil?
- Answer
-
100.04°C, or 100°C to three significant figures. (Recall that 1 mol of \(\ce{NaCl}\) produces 2 mol of dissolved particles. The small increase in temperature means that adding salt to the water used to cook pasta has essentially no effect on the cooking time.)
Freezing Point Depression
The phase diagram in Figure \(\PageIndex{1}\) shows that dissolving a nonvolatile solute in water not only raises the boiling point of the water but also lowers its freezing point. The solid–liquid curve for the solution crosses the line corresponding to P = 1 atm at a lower temperature than the curve for pure water.
This phenomenon is exploited in “de-icing” schemes that use salt (Figure \(\PageIndex{3}\)), calcium chloride, or urea to melt ice on roads and sidewalks, and in the use of ethylene glycol as an “antifreeze” in automobile radiators. Seawater freezes at a lower temperature than fresh water, and so the Arctic and Antarctic oceans remain unfrozen even at temperatures below 0 °C (as do the body fluids of fish and other cold-blooded sea animals that live in these oceans).

We can understand this result by imagining that we have a sample of water at the normal freezing point temperature, where there is a dynamic equilibrium between solid and liquid. Water molecules are continuously colliding with the ice surface and entering the solid phase at the same rate that water molecules are leaving the surface of the ice and entering the liquid phase. If we dissolve a nonvolatile solute such as glucose in the liquid, the dissolved glucose molecules will reduce the number of collisions per unit time between water molecules and the ice surface because some of the molecules colliding with the ice will be glucose. Glucose, though, has a very different structure than water, and it cannot fit into the ice lattice. Consequently, the presence of glucose molecules in the solution can only decrease the rate at which water molecules in the liquid collide with the ice surface and solidify. Meanwhile, the rate at which the water molecules leave the surface of the ice and enter the liquid phase is unchanged. The net effect is to cause the ice to melt. The only way to reestablish a dynamic equilibrium between solid and liquid water is to lower the temperature of the system, which decreases the rate at which water molecules leave the surface of the ice crystals until it equals the rate at which water molecules in the solution collide with the ice.
By analogy to our treatment of boiling point elevation,the freezing point depression (\(ΔT_f\)) is defined as the difference between the freezing point of the pure solvent and the freezing point of the solution:
\[ ΔT_f=T^0_f−T_f \label{eq3}\]
where
- \(T^0_f\) is the freezing point of the pure solvent and
- \(T_f\) is the freezing point of the solution.
The order of the terms is reversed compared with Equation \ref{eq1} to express the freezing point depression as a positive number. The relationship between \(ΔT_f\) and the solute concentration is given by an equation analogous to Equation \ref{eq2}:
\[ΔT_f = mK_f \label{eq4}\]
where
- \(m\) is the molality of the solution and
- \(K_f\) is the molal freezing point depression constant for the solvent (in units of °C/m).
Like \(K_b\), each solvent has a characteristic value of \(K_f\) (Table \(\PageIndex{1}\)). Freezing point depression depends on the total number of dissolved nonvolatile solute particles, just as with boiling point elevation. Thus an aqueous \(\ce{NaCl}\) solution has twice as large a freezing point depression as a glucose solution of the same molality.
People who live in cold climates use freezing point depression to their advantage in many ways. For example, ethylene glycol is added to engine coolant water to prevent an automobile engine from being destroyed, and methanol is added to windshield washer fluid to prevent the fluid from freezing. Heated glycols are often sprayed onto the surface of airplanes prior to takeoff in inclement weather in the winter to remove ice that has already formed and prevent the formation of more ice, which would be particularly dangerous if formed on the control surfaces of the aircraft (Video \(\PageIndex{1}\)).
Video \(\PageIndex{1}\): Freezing point depression is exploited to remove ice from the control surfaces of aircraft.
The decrease in vapor pressure, increase in boiling point, and decrease in freezing point of a solution versus a pure liquid all depend on the total number of dissolved nonvolatile solute particles.
In colder regions of the United States, \(\ce{NaCl}\) or \(\ce{CaCl_2}\) is often sprinkled on icy roads in winter to melt the ice and make driving safer. Use the data in Figure 13.9 to estimate the concentrations of two saturated solutions at 0°C, one of \(\ce{NaCl}\) and one of \(\ce{CaCl_2}\), and calculate the freezing points of both solutions to see which salt is likely to be more effective at melting ice.
Given: solubilities of two compounds
Asked for: concentrations and freezing points
Strategy:
- Estimate the solubility of each salt in 100 g of water from Figure 13.9. Determine the number of moles of each in 100 g and calculate the molalities.
- Determine the concentrations of the dissolved salts in the solutions. Substitute these values into Equation \(\PageIndex{4}\) to calculate the freezing point depressions of the solutions.
Solution:
A From Figure 13.9, we can estimate the solubilities of \(\ce{NaCl}\) and \(\ce{CaCl_2}\) to be about 36 g and 60 g, respectively, per 100 g of water at 0°C. The corresponding concentrations in molality are
\[m_{\ce{NaCl}}=\left(\dfrac{36 \; \cancel{g \;NaCl}}{100 \;\cancel{g} \;H_2O}\right)\left(\dfrac{1\; mol\; NaCl}{58.44\; \cancel{ g\; NaCl}}\right)\left(\dfrac{1000\; \cancel{g}}{1\; kg}\right)=6.2\; m\]
\[m_{\ce{CaCl_2}}=\left(\dfrac{60\; \cancel{g\; CaCl_2}}{100\;\cancel{g}\; H_2O}\right)\left(\dfrac{1\; mol\; CaCl_2}{110.98\; \cancel{g\; CaCl_2}}\right)\left(\dfrac{1000 \;\cancel{g}}{1 kg}\right)=5.4\; m\]
The lower formula mass of \(\ce{NaCl}\) more than compensates for its lower solubility, resulting in a saturated solution that has a slightly higher concentration than \(\ce{CaCl_2}\).
B Because these salts are ionic compounds that dissociate in water to yield two and three ions per formula unit of \(\ce{NaCl}\) and \(\ce{CaCl_2}\), respectively, the actual concentrations of the dissolved species in the two saturated solutions are 2 × 6.2 m = 12 m for \(\ce{NaCl}\) and 3 × 5.4 m = 16 m for \(\ce{CaCl_2}\). The resulting freezing point depressions can be calculated using Equation \(\PageIndex{4}\):
\[\ce{NaCl}: ΔT_f=mK_f=(12\; \cancel{m})(1.86°C/\cancel{m})=22°C\]
\[\ce{CaCl2}: ΔT_f=mK_f=(16\;\cancel{m})(1.86°C/\cancel{m})=30°C\]
Because the freezing point of pure water is 0°C, the actual freezing points of the solutions are −22°C and −30°C, respectively. Note that \(\ce{CaCl_2}\) is substantially more effective at lowering the freezing point of water because its solutions contain three ions per formula unit. In fact, \(\ce{CaCl_2}\) is the salt usually sold for home use, and it is also often used on highways.
Because the solubilities of both salts decrease with decreasing temperature, the freezing point can be depressed by only a certain amount, regardless of how much salt is spread on an icy road. If the temperature is significantly below the minimum temperature at which one of these salts will cause ice to melt (say −35°C), there is no point in using salt until it gets warmer
Calculate the freezing point of the 30.2% solution of ethylene glycol in water whose vapor pressure and boiling point we calculated in Example \(\PageIndex{6}\).8 and Example \(\PageIndex{6}\).10.
- Answer
-
−13.0°C
Arrange these aqueous solutions in order of decreasing freezing points: 0.1 m \(KCl\), 0.1 m glucose, 0.1 m SrCl2, 0.1 m ethylene glycol, 0.1 m benzoic acid, and 0.1 m HCl.
Given: molalities of six solutions
Asked for: relative freezing points
Strategy:
- Identify each solute as a strong, weak, or nonelectrolyte, and use this information to determine the number of solute particles produced.
- Multiply this number by the concentration of the solution to obtain the effective concentration of solute particles. The solution with the highest effective concentration of solute particles has the largest freezing point depression.
Solution:
A Because the molal concentrations of all six solutions are the same, we must focus on which of the substances are strong electrolytes, which are weak electrolytes, and which are nonelectrolytes to determine the actual numbers of particles in solution. \(KCl\), \(SrCl_2\), and \(HCl\) are strong electrolytes, producing two, three, and two ions per formula unit, respectively. Benzoic acid is a weak electrolyte (approximately one particle per molecule), and glucose and ethylene glycol are both nonelectrolytes (one particle per molecule).
B The molalities of the solutions in terms of the total particles of solute are: \(KCl\) and \(HCl\), 0.2 m; \(SrCl_2\), 0.3 m; glucose and ethylene glycol, 0.1 m; and benzoic acid, 0.1–0.2 m. Because the magnitude of the decrease in freezing point is proportional to the concentration of dissolved particles, the order of freezing points of the solutions is: glucose and ethylene glycol (highest freezing point, smallest freezing point depression) > benzoic acid > \(HCl\) = \(KCl\) > \(SrCl_2\).
Arrange these aqueous solutions in order of increasing freezing points: 0.2 m \(NaCl\), 0.3 m acetic acid, 0.1 m \(\ce{CaCl_2}\), and 0.2 m sucrose.
- Answer
-
0.2 m \(\ce{NaCl}\) (lowest freezing point) < 0.3 m acetic acid ≈ 0.1 m \(\ce{CaCl_2}\) < 0.2 m sucrose (highest freezing point)
Boiling Point Elevation and Freezing Point Depression: https://youtu.be/0MZm1Ay6LhU
Determination of Molar Masses
Osmotic pressure and changes in freezing point, boiling point, and vapor pressure are directly proportional to the concentration of solute present. Consequently, we can use a measurement of one of these properties to determine the molar mass of the solute from the measurements.
A solution of 4.00 g of a nonelectrolyte dissolved in 55.0 g of benzene is found to freeze at 2.32 °C. What is the molar mass of this compound?
Solution
We can solve this problem using the following steps.
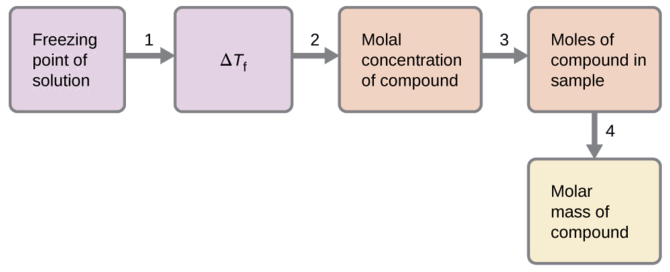
- Determine the change in freezing point from the observed freezing point and the freezing point of pure benzene (Table \(\PageIndex{1}\)).
\(ΔT_\ce{f}=\mathrm{5.5\:°C−2.32\:°C=3.2\:°C}\)
- Determine the molal concentration from Kf, the freezing point depression constant for benzene (Table \(\PageIndex{1}\)), and ΔTf.
\(ΔT_\ce{f}=K_\ce{f}m\)
\(m=\dfrac{ΔT_\ce{f}}{K_\ce{f}}=\dfrac{3.2\:°\ce C}{5.12\:°\ce C m^{−1}}=0.63\:m\) - Determine the number of moles of compound in the solution from the molal concentration and the mass of solvent used to make the solution.
\(\mathrm{Moles\: of\: solute=\dfrac{0.62\:mol\: solute}{1.00\cancel{kg\: solvent}}×0.0550\cancel{kg\: solvent}=0.035\:mol}\)
- Determine the molar mass from the mass of the solute and the number of moles in that mass.
\(\mathrm{Molar\: mass=\dfrac{4.00\:g}{0.034\:mol}=1.2×10^2\:g/mol}\)
A solution of 35.7 g of a nonelectrolyte in 220.0 g of chloroform has a boiling point of 64.5 °C. What is the molar mass of this compound?
- Answer
-
1.8 × 102 g/mol
A 0.500 L sample of an aqueous solution containing 10.0 g of hemoglobin has an osmotic pressure of 5.9 torr at 22 °C. What is the molar mass of hemoglobin?
Solution
Here is one set of steps that can be used to solve the problem:

- Convert the osmotic pressure to atmospheres, then determine the molar concentration from the osmotic pressure.
\[\Pi=\mathrm{\dfrac{5.9\:torr×1\:atm}{760\:torr}=7.8×10^{−3}\:atm}\]
\[\Pi=MRT\]
\(M=\dfrac{Π}{RT}=\mathrm{\dfrac{7.8×10^{−3}\:atm}{(0.08206\:L\: atm/mol\: K)(295\:K)}=3.2×10^{−4}\:M}\)
- Determine the number of moles of hemoglobin in the solution from the concentration and the volume of the solution.
\(\mathrm{moles\: of\: hemoglobin=\dfrac{3.2×10^{−4}\:mol}{1\cancel{L\: solution}}×0.500\cancel{L\: solution}=1.6×10^{−4}\:mol}\)
- Determine the molar mass from the mass of hemoglobin and the number of moles in that mass.
\(\mathrm{molar\: mass=\dfrac{10.0\:g}{1.6×10^{−4}\:mol}=6.2×10^4\:g/mol}\)
What is the molar mass of a protein if a solution of 0.02 g of the protein in 25.0 mL of solution has an osmotic pressure of 0.56 torr at 25 °C?
- Answer
-
2.7 × 104 g/mol
Finding the Molecular Weight of an Unknown using Colligative Properties:
Summary
- vapor pressure lowering: \[P^0_A−P_A=ΔP_A=X_BP^0_A \]
- vapor pressure of a system containing two volatile components: \[P_T=X_AP^0_A+(1−X_A)P^0_B \]
- boiling point elevation: \[ΔT_b = mK_b\]
- freezing point depression: \[ΔT_f = mK_f \]
The colligative properties of a solution depend on only the total number of dissolved particles in solution, not on their chemical identity. Colligative properties include vapor pressure, boiling point, freezing point, and osmotic pressure. The addition of a nonvolatile solute (one without a measurable vapor pressure) decreases the vapor pressure of the solvent. The vapor pressure of the solution is proportional to the mole fraction of solvent in the solution, a relationship known as Raoult’s law. Solutions that obey Raoult’s law are called ideal solutions. Most real solutions exhibit positive or negative deviations from Raoult’s law. The boiling point elevation (\(ΔT_b\)) and freezing point depression (\(ΔT_f\)) of a solution are defined as the differences between the boiling and freezing points, respectively, of the solution and the pure solvent. Both are proportional to the molality of the solute.

