13.4: Solution Formation and Equilibrium
- Page ID
- 42235
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To understand the relationship among temperature, pressure, and solubility.
- The understand that the solubility of a solid may increase or decrease with increasing temperature,
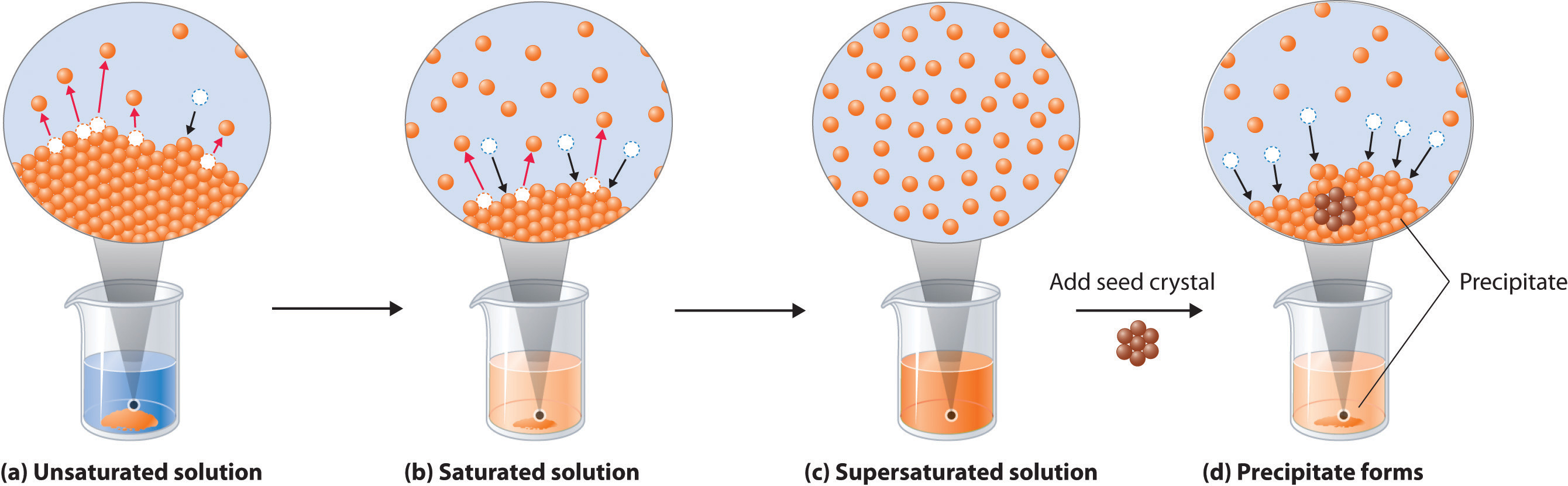
When a solute dissolves, its individual atoms, molecules, or ions interact with the solvent, become solvated, and are able to diffuse independently throughout the solution (part (a) in Figure \(\PageIndex{1}\)). This is not, however, a unidirectional process. If the molecule or ion happens to collide with the surface of a particle of the undissolved solute, it may adhere to the particle in a process called crystallization. Dissolution and crystallization continue as long as excess solid is present, resulting in a dynamic equilibrium analogous to the equilibrium that maintains the vapor pressure of a liquid. We can represent these opposing processes as follows:
\[ \text{solute} + \text{solvent} \ce{<=>[\ce{crystallization}][\ce{dissolution}]} \text{solution} \label{13.4.1} \]
Although the terms precipitation and crystallization are both used to describe the separation of solid solute from a solution, crystallization refers to the formation of a solid with a well-defined crystalline structure, whereas precipitation refers to the formation of any solid phase, often one with very small particles.
Solubility as a Function of Temperature
Figure \(\PageIndex{2}\) shows plots of the solubilities of several organic and inorganic compounds in water as a function of temperature. Although the solubility of a solid generally increases with increasing temperature, there is no simple relationship between the structure of a substance and the temperature dependence of its solubility. Many compounds (such as glucose and \(CH_3CO_2Na\)) exhibit a dramatic increase in solubility with increasing temperature. Others (such as \(NaCl\) and \(K_2SO_4\)) exhibit little variation, and still others (such as \(Li_2SO_4\)) become less soluble with increasing temperature.
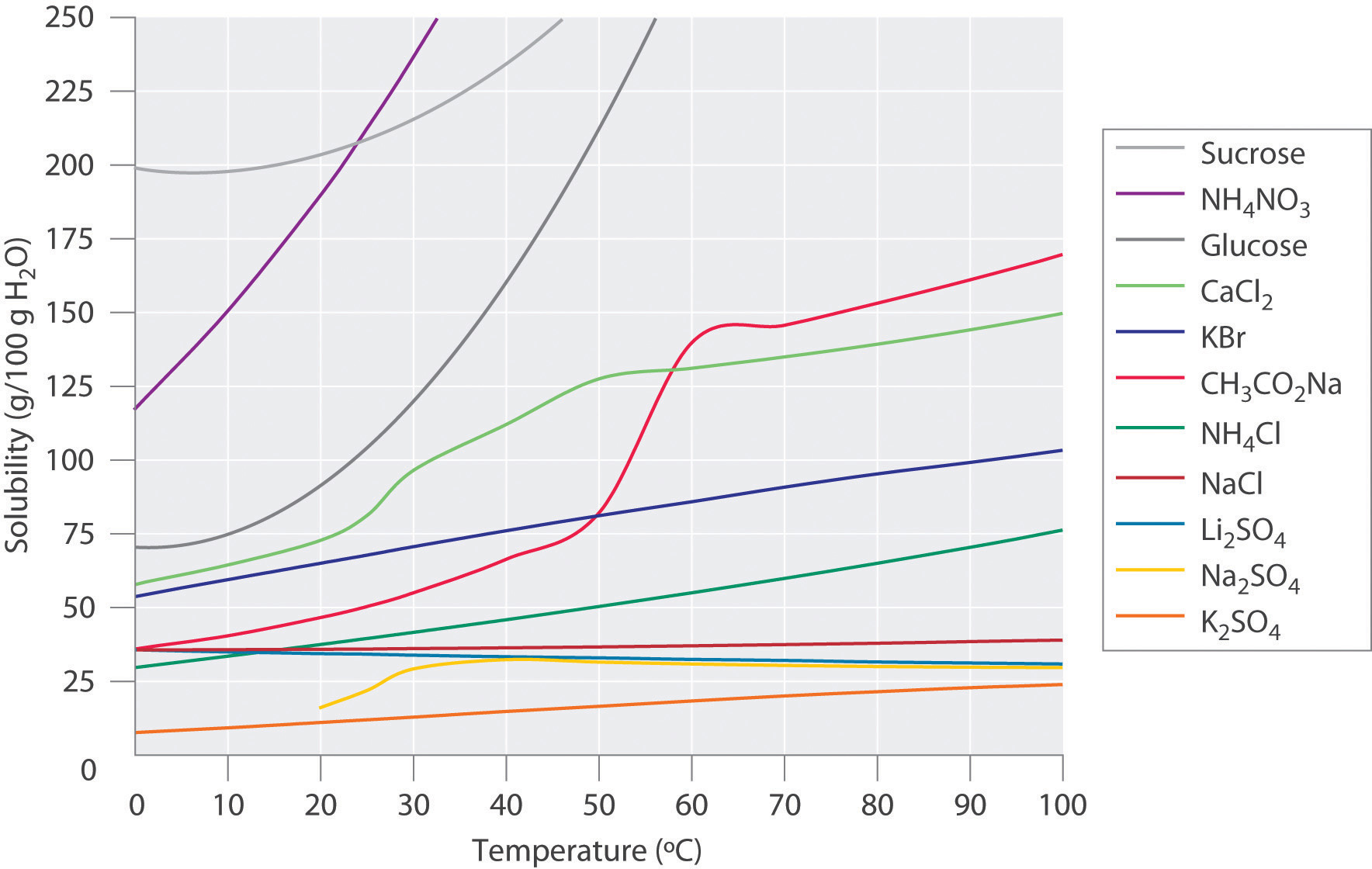
Notice in particular the curves for \(NH_4NO_3\) and \(CaCl_2\). The dissolution of ammonium nitrate in water is endothermic (\(ΔH_{soln} = +25.7\; kJ/mol\)), whereas the dissolution of calcium chloride is exothermic (\(ΔH_{soln} = −68.2 \;kJ/mol\)), yet Figure \(\PageIndex{2}\) shows that the solubility of both compounds increases sharply with increasing temperature. In fact, the magnitudes of the changes in both enthalpy and entropy for dissolution are temperature dependent. Because the solubility of a compound is ultimately determined by relatively small differences between large numbers, there is generally no good way to predict how the solubility will vary with temperature.
Fractional Crystallization
The variation of solubility with temperature has been measured for a wide range of compounds, and the results are published in many standard reference books. Chemists are often able to use this information to separate the components of a mixture by fractional crystallization, the separation of compounds on the basis of their solubilities in a given solvent (Figure \(\PageIndex{3}\)). For example, if we have a mixture of 150 g of sodium acetate (\(CH_3CO_2Na\)) and 50 g of \(KBr\), we can separate the two compounds by dissolving the mixture in 100 g of water at 80°C and then cooling the solution slowly to 0°C. According to the temperature curves in Figure \(\PageIndex{2}\), both compounds dissolve in water at 80°C, and all 50 g of \(KBr\) remains in solution at 0°C. Only about 36 g of \(CH_3CO_2Na\) are soluble in 100 g of water at 0°C, however, so approximately 114 g (150 g − 36 g) of \(CH_3CO_2Na\) crystallizes out on cooling. The crystals can then be separated by filtration. Thus fractional crystallization allows us to recover about 75% of the original \(CH_3CO_2Na\) in essentially pure form in only one step.
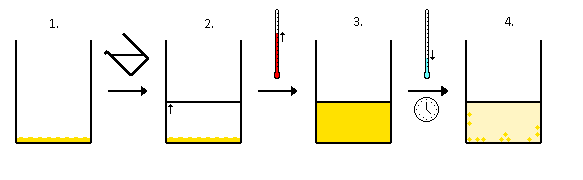
Fractional crystallization is a common technique for purifying compounds as diverse as those shown in Figure \(\PageIndex{2}\) and from antibiotics to enzymes to drugs (Figure \(\PageIndex{4}\)). For the technique to work properly, the compound of interest must be more soluble at high temperature than at low temperature, so that lowering the temperature causes it to crystallize out of solution. In addition, the impurities must be more soluble than the compound of interest (as was \(KBr\) in this example) and preferably present in relatively small amounts.
Summary
When a solution contains the maximum amount of solute that can dissolve under a given set of conditions, it is a saturated solution. Otherwise, it is unsaturated. Supersaturated solutions, which contain more dissolved solute than allowed under particular conditions, are not stable; the addition of a seed crystal, a small particle of solute, will usually cause the excess solute to crystallize. A system in which crystallization and dissolution occur at the same rate is in dynamic equilibrium. The solubility of most substances depends strongly on the temperature. The solubility of most solid or liquid solutes increases with increasing temperature. The components of a mixture can often be separated using fractional crystallization, which separates compounds according to their solubilities. The solubility of a gas decreases with increasing temperature.

