12.2: Some Properties of Liquids
- Page ID
- 6389
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Skills to Develop
- To describe the unique properties of liquids.
- To know how and why the vapor pressure of a liquid varies with temperature.
- To understand that the equilibrium vapor pressure of a liquid depends on the temperature and the intermolecular forces present.
- To understand that the relationship between pressure, enthalpy of vaporization, and temperature is given by the Clausius-Clapeyron equation.
Although you have been introduced to some of the interactions that hold molecules together in a liquid, we have not yet discussed the consequences of those interactions for the bulk properties of liquids. We now turn our attention to three unique properties of liquids that intimately depend on the nature of intermolecular interactions:
- surface tension,
- capillary action, and
- viscosity.
Surface Tension
If liquids tend to adopt the shapes of their containers, then, do small amounts of water on a freshly waxed car form raised droplets instead of a thin, continuous film? The answer lies in a property called surface tension, which depends on intermolecular forces. Surface tension is the energy required to increase the surface area of a liquid by a unit amount and varies greatly from liquid to liquid based on the nature of the intermolecular forces, e.g., water with hydrogen bonds has a surface tension of 7.29 x 10-2 J/m2 (at 20°C), while mercury with metallic (electrostatic) bonds has as surface tension that is 15-times lower: 4.6 x 10-1 J/m2 (at 20°C).
Figure \(\PageIndex{1}\) presents a microscopic view of a liquid droplet. A typical molecule in the interior of the droplet is surrounded by other molecules that exert attractive forces from all directions. Consequently, there is no net force on the molecule that would cause it to move in a particular direction. In contrast, a molecule on the surface experiences a net attraction toward the drop because there are no molecules on the outside to balance the forces exerted by adjacent molecules in the interior. Because a sphere has the smallest possible surface area for a given volume, intermolecular attractive interactions between water molecules cause the droplet to adopt a spherical shape. This maximizes the number of attractive interactions and minimizes the number of water molecules at the surface. Hence raindrops are almost spherical, and drops of water on a waxed (nonpolar) surface, which does not interact strongly with water, form round beads (see the chapter opener photo). A dirty car is covered with a mixture of substances, some of which are polar. Attractive interactions between the polar substances and water cause the water to spread out into a thin film instead of forming beads.
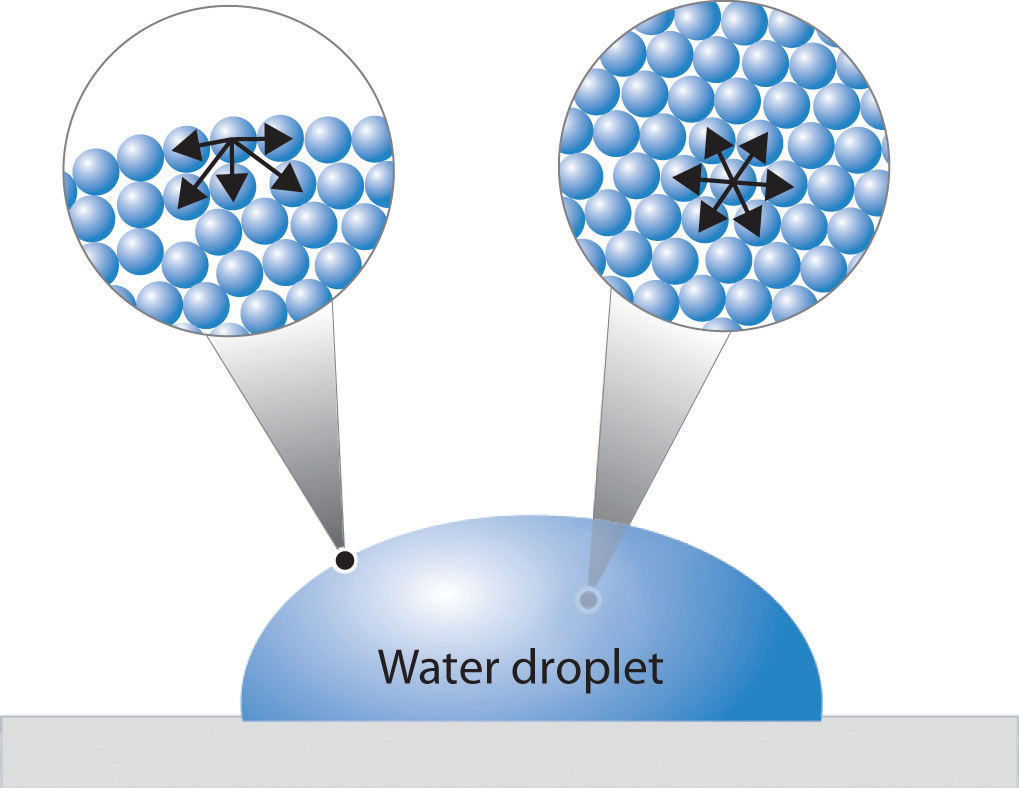
Figure \(\PageIndex{1}\): A Representation of Surface Tension in a Liquid. Molecules at the surface of water experience a net attraction to other molecules in the liquid, which holds the surface of the bulk sample together. In contrast, those in the interior experience uniform attractive forces.
The same phenomenon holds molecules together at the surface of a bulk sample of water, almost as if they formed a skin. When filling a glass with water, the glass can be overfilled so that the level of the liquid actually extends above the rim. Similarly, a sewing needle or a paper clip can be placed on the surface of a glass of water where it “floats,” even though steel is much denser than water. Many insects take advantage of this property to walk on the surface of puddles or ponds without sinking. This is even better describe in the zero gravity condictions of space as Figure \(\PageIndex{2}\) indicates (and more so in the video link).
Figure \(\PageIndex{2}\): The Effects of the High Surface Tension of Liquid Water. The Full video can be found at https://www.youtube.com/watch?v=9jB7rOC5kG8.
Such phenomena are manifestations of surface tension, which is defined as the energy required to increase the surface area of a liquid by a specific amount. Surface tension is therefore measured as energy per unit area, such as joules per square meter (J/m2) or dyne per centimeter (dyn/cm), where 1 dyn = 1 × 10−5 N. The values of the surface tension of some representative liquids are listed in Table \(\PageIndex{1}\). Note the correlation between the surface tension of a liquid and the strength of the intermolecular forces: the stronger the intermolecular forces, the higher the surface tension. For example, water, with its strong intermolecular hydrogen bonding, has one of the highest surface tension values of any liquid, whereas low-boiling-point organic molecules, which have relatively weak intermolecular forces, have much lower surface tensions. Mercury is an apparent anomaly, but its very high surface tension is due to the presence of strong metallic bonding.
| Substance | Surface Tension (× 10−3 J/m2) | Viscosity (mPa•s) | Vapor Pressure (mmHg) | Normal Boiling Point (°C) |
|---|---|---|---|---|
| Organic Compounds | ||||
| diethyl ether | 17 | 0.22 | 531 | 34.6 |
| n-hexane | 18 | 0.30 | 149 | 68.7 |
| acetone | 23 | 0.31 | 227 | 56.5 |
| ethanol | 22 | 1.07 | 59 | 78.3 |
| ethylene glycol | 48 | 16.1 | ~0.08 | 198.9 |
| Liquid Elements | ||||
| bromine | 41 | 0.94 | 218 | 58.8 |
| mercury | 486 | 1.53 | 0.0020 | 357 |
| Water | ||||
| 0°C | 75.6 | 1.79 | 4.6 | — |
| 20°C | 72.8 | 1.00 | 17.5 | — |
| 60°C | 66.2 | 0.47 | 149 | — |
| 100°C | 58.9 | 0.28 | 760 | — |
Adding soaps and detergents that disrupt the intermolecular attractions between adjacent water molecules can reduce the surface tension of water. Because they affect the surface properties of a liquid, soaps and detergents are called surface-active agents, or surfactants. In the 1960s, US Navy researchers developed a method of fighting fires aboard aircraft carriers using “foams,” which are aqueous solutions of fluorinated surfactants. The surfactants reduce the surface tension of water below that of fuel, so the fluorinated solution is able to spread across the burning surface and extinguish the fire. Such foams are now used universally to fight large-scale fires of organic liquids.
Capillary Action
Intermolecular forces also cause a phenomenon called capillary action, which is the tendency of a polar liquid to rise against gravity into a small-diameter tube (a capillary), as shown in Figure \(\PageIndex{3}\). When a glass capillary is put into a dish of water, water is drawn up into the tube. The height to which the water rises depends on the diameter of the tube and the temperature of the water but not on the angle at which the tube enters the water. The smaller the diameter, the higher the liquid rises.

Figure \(\PageIndex{3}\): The Phenomenon of Capillary Action. Capillary action seen as water climbs to different levels in glass tubes of different diameters. Credit: Dr. Clay Robinson, PhD, West Texas A&M University.
When a glass capillary is placed in liquid water, water rises up into the capillary. The smaller the diameter of the capillary, the higher the water rises. The height of the water does not depend on the angle at which the capillary is tilted.
Note
- Cohesive forces bind molecules of the same type together
- Adhesive forces bind a substance to a surface
The same phenomenon holds molecules together at the surface of a bulk sample of water, almost as if they formed a skin. When filling a glass with water, the glass can be overfilled so that the level of the liquid actually extends
Capillary action is the net result of two opposing sets of forces: cohesive forces, which are the intermolecular forces that hold a liquid together, and adhesive forces, which are the attractive forces between a liquid and the substance that composes the capillary. Water has both strong adhesion to glass, which contains polar SiOH groups, and strong intermolecular cohesion. When a glass capillary is put into water, the surface tension due to cohesive forces constricts the surface area of water within the tube, while adhesion between the water and the glass creates an upward force that maximizes the amount of glass surface in contact with the water. If the adhesive forces are stronger than the cohesive forces, as is the case for water, then the liquid in the capillary rises to the level where the downward force of gravity exactly balances this upward force. If, however, the cohesive forces are stronger than the adhesive forces, as is the case for mercury and glass, the liquid pulls itself down into the capillary below the surface of the bulk liquid to minimize contact with the glass (part (a) in Figure \(\PageIndex{4}\)). The upper surface of a liquid in a tube is called the meniscus, and the shape of the meniscus depends on the relative strengths of the cohesive and adhesive forces. In liquids such as water, the meniscus is concave; in liquids such as mercury, however, which have very strong cohesive forces and weak adhesion to glass, the meniscus is convex (part (b) in Figure \(\PageIndex{4}\)).
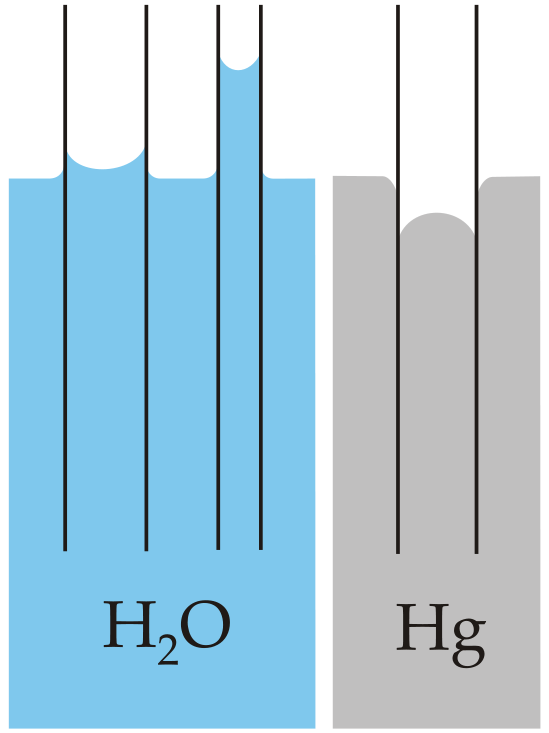
Figure \(\PageIndex{4}\): The Phenomenon of Capillary Action. Capillary action of water compared to mercury, in each case with respect to a polar surface such as glass. (a) This drawing illustrates the shape of the meniscus and the relative height of a mercury column when a glass capillary is put into liquid mercury. The meniscus is convex and the surface of the liquid inside the tube is lower than the level of the liquid outside the tube. (b) Because water adheres strongly to the polar surface of glass, it has a concave meniscus, whereas mercury, which does not adhere to the glass, has a convex meniscus. Figure used with permission from Wikipedia.
Note
Polar substances are drawn up a glass capillary and generally have a concave meniscus.
Fluids and nutrients are transported up the stems of plants or the trunks of trees by capillary action. Plants contain tiny rigid tubes composed of cellulose, to which water has strong adhesion. Because of the strong adhesive forces, nutrients can be transported from the roots to the tops of trees that are more than 50 m tall. Cotton towels are also made of cellulose; they absorb water because the tiny tubes act like capillaries and “wick” the water away from your skin. The moisture is absorbed by the entire fabric, not just the layer in contact with your body.
Viscosity
Viscosity (η) is the resistance of a liquid to flow. Some liquids, such as gasoline, ethanol, and water, flow very readily and hence have a low viscosity. Others, such as motor oil, molasses, and maple syrup, flow very slowly and have a high viscosity. The two most common methods for evaluating the viscosity of a liquid are (1) to measure the time it takes for a quantity of liquid to flow through a narrow vertical tube and (2) to measure the time it takes steel balls to fall through a given volume of the liquid. The higher the viscosity, the slower the liquid flows through the tube and the steel balls fall. Viscosity is expressed in units of the poise (mPa•s); the higher the number, the higher the viscosity. The viscosities of some representative liquids are listed in Table \(\PageIndex{1}\) and show a correlation between viscosity and intermolecular forces. Because a liquid can flow only if the molecules can move past one another with minimal resistance, strong intermolecular attractive forces make it more difficult for molecules to move with respect to one another. The addition of a second hydroxyl group to ethanol, for example, which produces ethylene glycol (HOCH2CH2OH), increases the viscosity 15-fold. This effect is due to the increased number of hydrogen bonds that can form between hydroxyl groups in adjacent molecules, resulting in dramatically stronger intermolecular attractive forces.
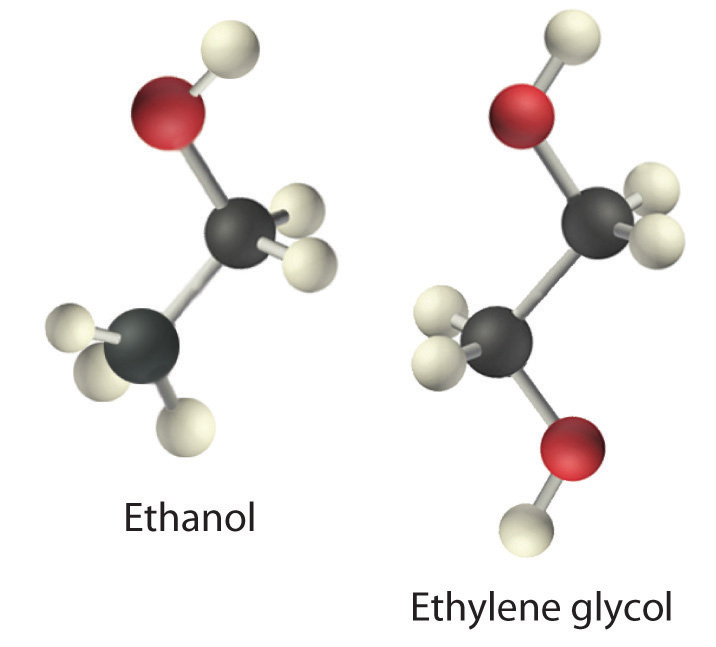
There is also a correlation between viscosity and molecular shape. Liquids consisting of long, flexible molecules tend to have higher viscosities than those composed of more spherical or shorter-chain molecules. The longer the molecules, the easier it is for them to become “tangled” with one another, making it more difficult for them to move past one another. London dispersion forces also increase with chain length. Due to a combination of these two effects, long-chain hydrocarbons (such as motor oils) are highly viscous.
Note
Viscosity increases as intermolecular interactions or molecular size increases.
Application: Motor Oils
Motor oils and other lubricants demonstrate the practical importance of controlling viscosity. The oil in an automobile engine must effectively lubricate under a wide range of conditions, from subzero starting temperatures to the 200°C that oil can reach in an engine in the heat of the Mojave Desert in August. Viscosity decreases rapidly with increasing temperatures because the kinetic energy of the molecules increases, and higher kinetic energy enables the molecules to overcome the attractive forces that prevent the liquid from flowing. As a result, an oil that is thin enough to be a good lubricant in a cold engine will become too “thin” (have too low a viscosity) to be effective at high temperatures.
Oil being drained from a car
The viscosity of motor oils is described by an SAE (Society of Automotive Engineers) rating ranging from SAE 5 to SAE 50 for engine oils: the lower the number, the lower the viscosity. So-called single-grade oils can cause major problems. If they are viscous enough to work at high operating temperatures (SAE 50, for example), then at low temperatures, they can be so viscous that a car is difficult to start or an engine is not properly lubricated. Consequently, most modern oils are multigrade, with designations such as SAE 20W/50 (a grade used in high-performance sports cars), in which case the oil has the viscosity of an SAE 20 oil at subzero temperatures (hence the W for winter) and the viscosity of an SAE 50 oil at high temperatures. These properties are achieved by a careful blend of additives that modulate the intermolecular interactions in the oil, thereby controlling the temperature dependence of the viscosity. Many of the commercially available oil additives “for improved engine performance” are highly viscous materials that increase the viscosity and effective SAE rating of the oil, but overusing these additives can cause the same problems experienced with highly viscous single-grade oils.
Example \(\PageIndex{1}\)
Based on the nature and strength of the intermolecular cohesive forces and the probable nature of the liquid–glass adhesive forces, predict what will happen when a glass capillary is put into a beaker of SAE 20 motor oil. Will the oil be pulled up into the tube by capillary action or pushed down below the surface of the liquid in the beaker? What will be the shape of the meniscus (convex or concave)? (Hint: the surface of glass is lined with Si–OH groups.)
Given: substance and composition of the glass surface
Asked for: behavior of oil and the shape of meniscus
Strategy:
- Identify the cohesive forces in the motor oil.
- Determine whether the forces interact with the surface of glass. From the strength of this interaction, predict the behavior of the oil and the shape of the meniscus.
Solution:
A Motor oil is a nonpolar liquid consisting largely of hydrocarbon chains. The cohesive forces responsible for its high boiling point are almost solely London dispersion forces between the hydrocarbon chains. B Such a liquid cannot form strong interactions with the polar Si–OH groups of glass, so the surface of the oil inside the capillary will be lower than the level of the liquid in the beaker. The oil will have a convex meniscus similar to that of mercury.
Exercise \(\PageIndex{1}\)
Predict what will happen when a glass capillary is put into a beaker of ethylene glycol. Will the ethylene glycol be pulled up into the tube by capillary action or pushed down below the surface of the liquid in the beaker? What will be the shape of the meniscus (convex or concave)?
Answer: Capillary action will pull the ethylene glycol up into the capillary. The meniscus will be concave.
Vapor Pressure
Nearly all of us have heated a pan of water with the lid in place and shortly thereafter heard the sounds of the lid rattling and hot water spilling onto the stovetop. When a liquid is heated, its molecules obtain sufficient kinetic energy to overcome the forces holding them in the liquid and they escape into the gaseous phase. By doing so, they generate a population of molecules in the vapor phase above the liquid that produces a pressure—the vapor pressure of the liquid. In the situation we described, enough pressure was generated to move the lid, which allowed the vapor to escape. If the vapor is contained in a sealed vessel, however, such as an unvented flask, and the vapor pressure becomes too high, the flask will explode (as many students have unfortunately discovered). In this section, we describe vapor pressure in more detail and explain how to quantitatively determine the vapor pressure of a liquid.
Evaporation and Condensation
Because the molecules of a liquid are in constant motion, we can plot the fraction of molecules with a given kinetic energy (KE) against their kinetic energy to obtain the kinetic energy distribution of the molecules in the liquid (Figure \(\PageIndex{5}\)), just as we did for a gas (Figure 10.19). As for gases, increasing the temperature increases both the average kinetic energy of the particles in a liquid and the range of kinetic energy of the individual molecules. If we assume that a minimum amount of energy (E0) is needed to overcome the intermolecular attractive forces that hold a liquid together, then some fraction of molecules in the liquid always has a kinetic energy greater than E0. The fraction of molecules with a kinetic energy greater than this minimum value increases with increasing temperature. Any molecule with a kinetic energy greater than E0 has enough energy to overcome the forces holding it in the liquid and escape into the vapor phase. Before it can do so, however, a molecule must also be at the surface of the liquid, where it is physically possible for it to leave the liquid surface; that is, only molecules at the surface can undergo evaporation (or vaporization), where molecules gain sufficient energy to enter a gaseous state above a liquid’s surface, thereby creating a vapor pressure.

Figure \(\PageIndex{5}\): The Distribution of the Kinetic Energies of the Molecules of a Liquid at Two Temperatures. Just as with gases, increasing the temperature shifts the peak to a higher energy and broadens the curve. Only molecules with a kinetic energy greater than E0 can escape from the liquid to enter the vapor phase, and the proportion of molecules with KE > E0 is greater at the higher temperature.
To understand the causes of vapor pressure, consider the apparatus shown in Figure \(\PageIndex{6}\). When a liquid is introduced into an evacuated chamber (part (a) in Figure \(\PageIndex{6}\)), the initial pressure above the liquid is approximately zero because there are as yet no molecules in the vapor phase. Some molecules at the surface, however, will have sufficient kinetic energy to escape from the liquid and form a vapor, thus increasing the pressure inside the container. As long as the temperature of the liquid is held constant, the fraction of molecules with KE > E0 will not change, and the rate at which molecules escape from the liquid into the vapor phase will depend only on the surface area of the liquid phase.

Figure \(\PageIndex{6}\): Vapor Pressure. (a) When a liquid is introduced into an evacuated chamber, molecules with sufficient kinetic energy escape from the surface and enter the vapor phase, causing the pressure in the chamber to increase. (b) When sufficient molecules are in the vapor phase for a given temperature, the rate of condensation equals the rate of evaporation (a steady state is reached), and the pressure in the container becomes constant.
As soon as some vapor has formed, a fraction of the molecules in the vapor phase will collide with the surface of the liquid and reenter the liquid phase in a process known as condensation (part (b) in Figure \(\PageIndex{6}\)). As the number of molecules in the vapor phase increases, the number of collisions between vapor-phase molecules and the surface will also increase. Eventually, a steady state will be reached in which exactly as many molecules per unit time leave the surface of the liquid (vaporize) as collide with it (condense). At this point, the pressure over the liquid stops increasing and remains constant at a particular value that is characteristic of the liquid at a given temperature. The rates of evaporation and condensation over time for a system such as this are shown graphically in Figure \(\PageIndex{7}\).
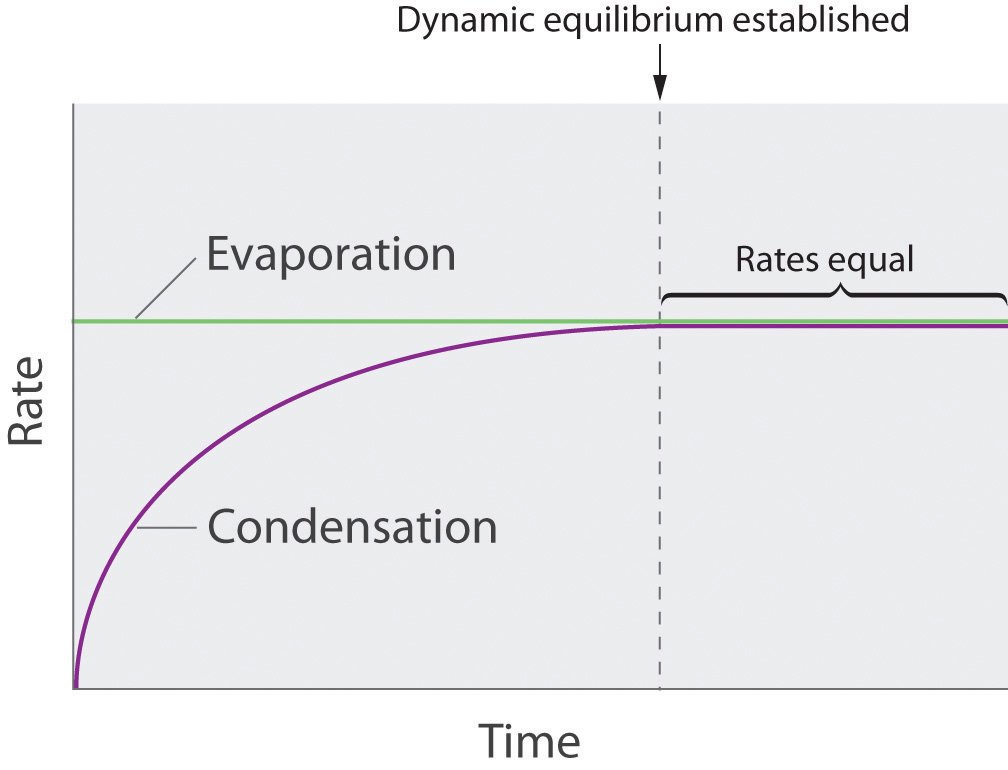
Figure \(\PageIndex{7}\): The Relative Rates of Evaporation and Condensation as a Function of Time after a Liquid Is Introduced into a Sealed Chamber. The rate of evaporation depends only on the surface area of the liquid and is essentially constant. The rate of condensation depends on the number of molecules in the vapor phase and increases steadily until it equals the rate of evaporation.
Equilibrium Vapor Pressure
Two opposing processes (such as evaporation and condensation) that occur at the same rate and thus produce no net change in a system, constitute a dynamic equilibrium. In the case of a liquid enclosed in a chamber, the molecules continuously evaporate and condense, but the amounts of liquid and vapor do not change with time. The pressure exerted by a vapor in dynamic equilibrium with a liquid is the equilibrium vapor pressure of the liquid.
If a liquid is in an open container, however, most of the molecules that escape into the vapor phase will not collide with the surface of the liquid and return to the liquid phase. Instead, they will diffuse through the gas phase away from the container, and an equilibrium will never be established. Under these conditions, the liquid will continue to evaporate until it has “disappeared.” The speed with which this occurs depends on the vapor pressure of the liquid and the temperature. Volatile liquids have relatively high vapor pressures and tend to evaporate readily; nonvolatile liquids have low vapor pressures and evaporate more slowly. Although the dividing line between volatile and nonvolatile liquids is not clear-cut, as a general guideline, we can say that substances with vapor pressures greater than that of water (Table 11.4) are relatively volatile, whereas those with vapor pressures less than that of water are relatively nonvolatile. Thus diethyl ether (ethyl ether), acetone, and gasoline are volatile, but mercury, ethylene glycol, and motor oil are nonvolatile.
The equilibrium vapor pressure of a substance at a particular temperature is a characteristic of the material, like its molecular mass, melting point, and boiling point (Table 11.4). It does not depend on the amount of liquid as long as at least a tiny amount of liquid is present in equilibrium with the vapor. The equilibrium vapor pressure does, however, depend very strongly on the temperature and the intermolecular forces present, as shown for several substances in Figure \(\PageIndex{8}\). Molecules that can hydrogen bond, such as ethylene glycol, have a much lower equilibrium vapor pressure than those that cannot, such as octane. The nonlinear increase in vapor pressure with increasing temperature is much steeper than the increase in pressure expected for an ideal gas over the corresponding temperature range. The temperature dependence is so strong because the vapor pressure depends on the fraction of molecules that have a kinetic energy greater than that needed to escape from the liquid, and this fraction increases exponentially with temperature. As a result, sealed containers of volatile liquids are potential bombs if subjected to large increases in temperature. The gas tanks on automobiles are vented, for example, so that a car won’t explode when parked in the sun. Similarly, the small cans (1–5 gallons) used to transport gasoline are required by law to have a pop-off pressure release.
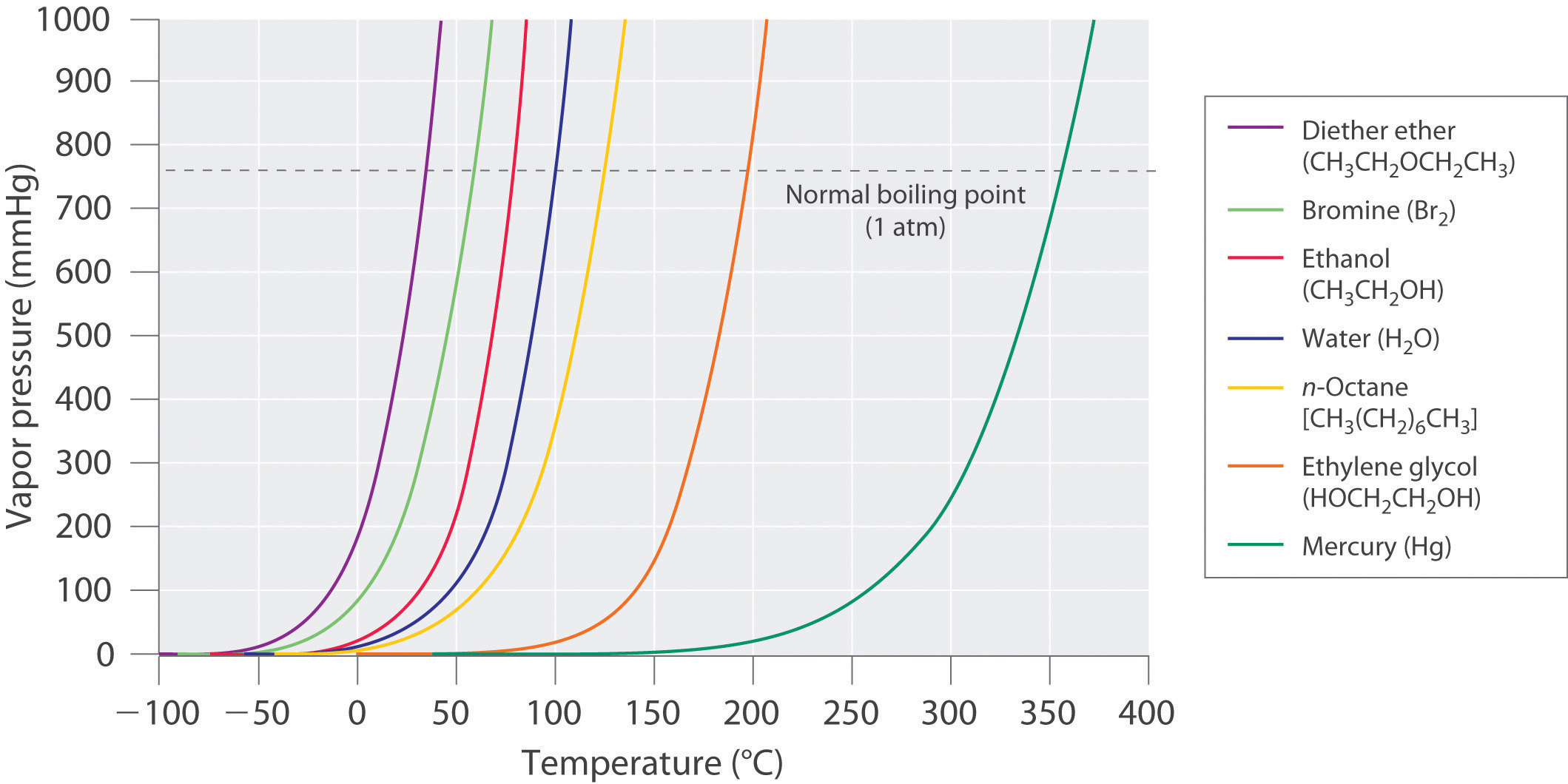
Figure \(\PageIndex{8}\): The Vapor Pressures of Several Liquids as a Function of Temperature. The point at which the vapor pressure curve crosses the P = 1 atm line (dashed) is the normal boiling point of the liquid.
Note
Volatile substances have low boiling points and relatively weak intermolecular interactions; nonvolatile substances have high boiling points and relatively strong intermolecular interactions.
\[ \ln\left ( P \right)=\dfrac{-\Delta H_{vap}}{R}\left ( \dfrac{1}{T} \right) + C \label{Eq1} \]
where
- \(\ln P\) is the natural logarithm of the vapor pressure,
- ΔHvap is the enthalpy of vaporization,
- R is the universal gas constant [8.314 J/(mol•K)],
- T is the temperature in kelvins, and
- C is the y-intercept, which is a constant for any given line.
A plot of \ln P versus the inverse of the absolute temperature (1/T) is a straight line with a slope of −ΔHvap/R. Equation \(\ref{Eq1}\), called the Clausius–Clapeyron equation, can be used to calculate the ΔHvap of a liquid from its measured vapor pressure at two or more temperatures. The simplest way to determine ΔHvap is to measure the vapor pressure of a liquid at two temperatures and insert the values of P and T for these points into Equation \(\ref{Eq1}\), which is derived from the Clausius–Clapeyron equation:
\[ \ln\left ( \dfrac{P_{1}}{P_{2}} \right)=\dfrac{-\Delta H_{vap}}{R}\left ( \dfrac{1}{T_{2}}-\dfrac{1}{T_{1}} \right) \tag{11.5.2} \]
Conversely, if we know ΔHvap and the vapor pressure P1 at any temperature T1, we can use Equation \(\ref{Eq1}\) to calculate the vapor pressure P2 at any other temperature T2, as shown in Example \(\PageIndex{2}\).
Example \(\PageIndex{2}\): Vapor Pressure of Mercury
The experimentally measured vapor pressures of liquid Hg at four temperatures are listed in the following table:
| T (°C) | 80.0 | 100 | 120 | 140 |
| P (torr) | 0.0888 | 0.2729 | 0.7457 | 1.845 |
From these data, calculate the enthalpy of vaporization (ΔHvap) of mercury and predict the vapor pressure of the liquid at 160°C. (Safety note: mercury is highly toxic; when it is spilled, its vapor pressure generates hazardous levels of mercury vapor.)
Given: vapor pressures at four temperatures
Asked for: ΔHvap of mercury and vapor pressure at 160°C
Strategy:
- Use Equation \(\ref{Eq1}\) to obtain ΔHvap directly from two pairs of values in the table, making sure to convert all values to the appropriate units.
- Substitute the calculated value of ΔHvap into Equation \(\ref{Eq1}\) to obtain the unknown pressure (P2).
Solution:
A The table gives the measured vapor pressures of liquid Hg for four temperatures. Although one way to proceed would be to plot the data using Equation \(\ref{Eq1}\) and find the value of ΔHvap from the slope of the line, an alternative approach is to use Equation \(\ref{Eq1}\) to obtain ΔHvap directly from two pairs of values listed in the table, assuming no errors in our measurement. We therefore select two sets of values from the table and convert the temperatures from degrees Celsius to kelvins because the equation requires absolute temperatures. Substituting the values measured at 80.0°C (T1) and 120.0°C (T2) into Equation \(\ref{Eq1}\) gives
\[ \ln\left ( \dfrac{0.7457 \; \cancel{Torr}}{0.0888 \; \cancel{Torr}} \right)=\dfrac{-\Delta H_{vap}}{8.314 \; J/mol\cdot K}\left ( \dfrac{1}{\left ( 120+273 \right)K}-\dfrac{1}{\left ( 80.0+273 \right)K} \right) \]
\[ \ln\left ( 8.398 \right)=\dfrac{-\Delta H_{vap}}{8.314 \; J/mol\cdot \cancel{K}}\left ( -2.88\times 10^{-4} \; \cancel{K^{-1}} \right) \]
\[ 2.13=-\Delta H_{vap} \left ( -3.46 \times 10^{-4} \right) J^{-1}\cdot mol \]
\[ \Delta H_{vap} =61,400 \; J/mol = 61.4 \; kJ/mol \]
B We can now use this value of ΔHvap to calculate the vapor pressure of the liquid (P2) at 160.0°C (T2):
\[ \ln\left ( \dfrac{P_{2} }{0.0888 \; torr} \right)=\dfrac{-61,400 \; \cancel{J/mol}}{8.314 \; \cancel{J/mol} \; K^{-1}}\left ( \dfrac{1}{\left ( 160+273 \right)K}-\dfrac{1}{\left ( 80.0+273 \right) K} \right) \]
Using the relationship e\ln x = x, we have
\[ \ln\left ( \dfrac{P_{2} }{0.0888 \; Torr} \right)=3.86 \]
\[ \dfrac{P_{2} }{0.0888 \; Torr} =e^{3.86} = 47.5 \]
\[ P_{2} = 4.21 Torr \]
At 160°C, liquid Hg has a vapor pressure of 4.21 torr, substantially greater than the pressure at 80.0°C, as we would expect.
Exercise \(\PageIndex{2}\): Vapor Pressure of Nickel
The vapor pressure of liquid nickel at 1606°C is 0.100 torr, whereas at 1805°C, its vapor pressure is 1.000 torr. At what temperature does the liquid have a vapor pressure of 2.500 torr?
Answer: 1896°C
Boiling Points
As the temperature of a liquid increases, the vapor pressure of the liquid increases until it equals the external pressure, or the atmospheric pressure in the case of an open container. Bubbles of vapor begin to form throughout the liquid, and the liquid begins to boil. The temperature at which a liquid boils at exactly 1 atm pressure is the normal boiling point of the liquid. For water, the normal boiling point is exactly 100°C. The normal boiling points of the other liquids in Figure \(\PageIndex{8}\) are represented by the points at which the vapor pressure curves cross the line corresponding to a pressure of 1 atm. Although we usually cite the normal boiling point of a liquid, the actual boiling point depends on the pressure. At a pressure greater than 1 atm, water boils at a temperature greater than 100°C because the increased pressure forces vapor molecules above the surface to condense. Hence the molecules must have greater kinetic energy to escape from the surface. Conversely, at pressures less than 1 atm, water boils below 100°C.
| Place | Altitude above Sea Level (ft) | Atmospheric Pressure (mmHg) | Boiling Point of Water (°C) |
|---|---|---|---|
| Mt. Everest, Nepal/Tibet | 29,028 | 240 | 70 |
| Bogota, Colombia | 11,490 | 495 | 88 |
| Denver, Colorado | 5280 | 633 | 95 |
| Washington, DC | 25 | 759 | 100 |
| Dead Sea, Israel/Jordan | −1312 | 799 | 101.4 |
Typical variations in atmospheric pressure at sea level are relatively small, causing only minor changes in the boiling point of water. For example, the highest recorded atmospheric pressure at sea level is 813 mmHg, recorded during a Siberian winter; the lowest sea-level pressure ever measured was 658 mmHg in a Pacific typhoon. At these pressures, the boiling point of water changes minimally, to 102°C and 96°C, respectively. At high altitudes, on the other hand, the dependence of the boiling point of water on pressure becomes significant. Table \(\PageIndex{2}\) lists the boiling points of water at several locations with different altitudes. At an elevation of only 5000 ft, for example, the boiling point of water is already lower than the lowest ever recorded at sea level. The lower boiling point of water has major consequences for cooking everything from soft-boiled eggs (a “three-minute egg” may well take four or more minutes in the Rockies and even longer in the Himalayas) to cakes (cake mixes are often sold with separate high-altitude instructions). Conversely, pressure cookers, which have a seal that allows the pressure inside them to exceed 1 atm, are used to cook food more rapidly by raising the boiling point of water and thus the temperature at which the food is being cooked.
Note
As pressure increases, the boiling point of a liquid increases and vice versa.
Example \(\PageIndex{3}\): Boiling Mercury
Use Figure \(\PageIndex{8}\) to estimate the following.
- the boiling point of water in a pressure cooker operating at 1000 mmHg
- the pressure required for mercury to boil at 250°C
Mercury boils at 356 °C at room pressure. To see video go to https://www.youtube.com/watch?v=0iizsbXWYoo
Given: data in Figure \(\PageIndex{8}\), pressure, and boiling point
Asked for: corresponding boiling point and pressure
Strategy:
- To estimate the boiling point of water at 1000 mmHg, refer to Figure \(\PageIndex{8}\) and find the point where the vapor pressure curve of water intersects the line corresponding to a pressure of 1000 mmHg.
- To estimate the pressure required for mercury to boil at 250°C, find the point where the vapor pressure curve of mercury intersects the line corresponding to a temperature of 250°C.
Solution:
- A The vapor pressure curve of water intersects the P = 1000 mmHg line at about 110°C; this is therefore the boiling point of water at 1000 mmHg.
- B The vertical line corresponding to 250°C intersects the vapor pressure curve of mercury at P ≈ 75 mmHg. Hence this is the pressure required for mercury to boil at 250°C.
Exercise \(\PageIndex{3}\): Boiling Ethlyene Glycol
Ethylene glycol is an organic compound primarily used as a raw material in the manufacture of polyester fibers and fabric industry, and polyethylene terephthalate resins (PET) used in bottling. Use the data in Figure \(\PageIndex{8}\) to estimate the following.
- the normal boiling point of ethylene glycol
- the pressure required for diethyl ether to boil at 20°C.
Answer
- 200°C
- 450 mmHg
Summary
- Surface tension, capillary action, and viscosity are unique properties of liquids that depend on the nature of intermolecular interactions.
Surface tension is the energy required to increase the surface area of a liquid by a given amount. The stronger the intermolecular interactions, the greater the surface tension. Surfactants are molecules, such as soaps and detergents, that reduce the surface tension of polar liquids like water. Capillary action is the phenomenon in which liquids rise up into a narrow tube called a capillary. It results when cohesive forces, the intermolecular forces in the liquid, are weaker than adhesive forces, the attraction between a liquid and the surface of the capillary. The shape of the meniscus, the upper surface of a liquid in a tube, also reflects the balance between adhesive and cohesive forces. The viscosity of a liquid is its resistance to flow. Liquids that have strong intermolecular forces tend to have high viscosities.
Because the molecules of a liquid are in constant motion and possess a wide range of kinetic energies, at any moment some fraction of them has enough energy to escape from the surface of the liquid to enter the gas or vapor phase. This process, called vaporization or evaporation, generates a vapor pressure above the liquid. Molecules in the gas phase can collide with the liquid surface and reenter the liquid via condensation. Eventually, a steady state is reached in which the number of molecules evaporating and condensing per unit time is the same, and the system is in a state of dynamic equilibrium. Under these conditions, a liquid exhibits a characteristic equilibrium vapor pressure that depends only on the temperature. We can express the nonlinear relationship between vapor pressure and temperature as a linear relationship using the Clausius–Clapeyron equation. This equation can be used to calculate the enthalpy of vaporization of a liquid from its measured vapor pressure at two or more temperatures. Volatile liquids are liquids with high vapor pressures, which tend to evaporate readily from an open container; nonvolatile liquids have low vapor pressures. When the vapor pressure equals the external pressure, bubbles of vapor form within the liquid, and it boils. The temperature at which a substance boils at a pressure of 1 atm is its normal boiling point.
Contributors and Attributions
Modified by Joshua Halpern (Howard University)
- Anonymous

