17.5: Express the Pressure in Terms of a Partition Function

Pressure can also be derived from the canonical partition function. The average pressure is the sum of the probability times the pressure:

\[ \langle P \rangle = \sum_i{P_i(N,V,T)P_i(N,V)} \nonumber \]

The pressure of a macroscopic system is:

\[ P(N,V) = -\left(\dfrac{\partial E_i}{\partial V}\right)_N \nonumber \]

So we can write the average pressure as:

\[\begin{split} \langle P \rangle &= \sum_i{P_i(N,V,\beta)\left(-\dfrac{\partial E_i}{\partial V}\right)_N} \\ &= \sum_i{\left(-\dfrac{\partial E_i}{\partial V}\right)_N\dfrac{e^{-E_i(N,V)/kT}}{Q(N,V,T)}} \end{split} \nonumber \]

In a few steps we can show that the temperature can be expressed in terms of the partition function:

\[ Q(N,V,T) = \sum_i{e^{-E_i(N,V)/kT}} \nonumber \]

Writing in terms of \(\beta\) instead of temperature:

\[ Q(N,V,\beta) = \sum_i{e^{-\beta E_i(N,V)}} \nonumber \]

The derivative of the partition function with respect to volume is:

\[ \left(\dfrac{\partial Q}{\partial V}\right)_{N,\beta} = -\beta \sum_i{\left(\dfrac{\partial E_i}{\partial V}\right)_{N}e^{-\beta E_i(N,V)}} \nonumber \]

The average pressure can then be written as:

\[ \langle P \rangle = \dfrac{kT}{Q(N,V,\beta}\left(\dfrac{\partial Q}{\partial V}\right)_{N,\beta} \nonumber \]

Which shows that the pressure can be expressed solely terms of the partition function:

\[ \langle P \rangle = kT\left(\dfrac{\partial \ln{Q}}{\partial V}\right)_{N,\beta} \nonumber \]

We can use this result to derive the ideal gas law. For \(N\) particles of an ideal gas:

\[ Q(N,V,\beta) = \dfrac{[q(V,\beta)]^N}{N!} \nonumber \]

where:

\[ q(V,\beta) = \left(\dfrac{2\pi m}{h^2\beta}\right)^{3/2}V \nonumber \]

is the translational partition function. The utility of expressing the pressure as a logarithm is clear from the fact that we can write:

\[\begin{split} \ln{Q} &= N\ln{q}-\ln{N!} \\ &= -\dfrac{3N}{2}\ln{\left(\dfrac{2\pi m}{h^2\beta}\right)}+N\ln{V}-\ln{N!} \end{split} \nonumber \]

We have used the property of logarithms that \(\ln{(AB)} = \ln{(A)} + \ln{(B)}\) and \(\ln{(X^Y)} = Y\ln{(X)}\). Only one term in the ln \(Q\) depends on \(V\). Taking the derivative of \(N\ln{V}\) with respect to \(V\) gives:

\[ \left(\dfrac{\partial \ln{Q}}{\partial V}\right)_{N,\beta} = \dfrac{N}{V} \nonumber \]

Substituting this into the above equation for the pressure gives:

\[ P = \dfrac{NkT}{V} \nonumber \]

which is the ideal gas law. Recall that \(Nk = nR\) where \(N\) is the number of molecules and \(n\) is the number of moles. \(R\) is the universal gas constant (8.314 J/mol-K) which is nothing more than \(k\) multiplied by Avagadro’s number. \(N_Ak = R\) converts the constant from a "per molecule" to a "per mole" basis.

Gas Compressed by a Piston

Figure 17.5.1 : Illustration of a thought experiment in which a system is compressed via a piston pushed into the system along the positive \(z\) axis.

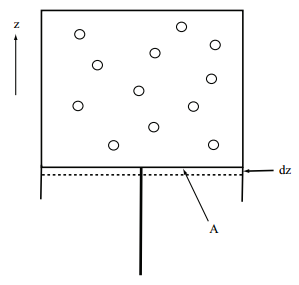
Let us consider a simple thought experiment, which is illustrated in the figure above: A system of \(N\) particles is compressed by a piston pushing in the positive \(z\) direction. Since this is a classical thought experiment, we think in terms of forces. The piston exerts a constant force of magnitude \(F\) on the system. The direction of the force is purely in the positive \(z\) direction, so that we can write the force vector \(\bf{F}\) as \(\bf{F} = \begin{pmatrix} 0, 0, F \end{pmatrix}\). At equilibrium (the piston is not moving), the system exerts an equal and opposite force on the piston of the form \(\begin{pmatrix} 0, 0, -F \end{pmatrix}\). If the energy of the system is \(E\), then the force exerted by the system on the piston will be given by the negative change in \(E\) with respect to \(z\):

\[-F = -\dfrac{dE}{dz} \label{Eq3.29} \]

or:

\[F = \dfrac{dE}{dz} \label{Eq3.30} \]

The force exerted by the system on the piston is manifest as an observable pressure \(P\) equal to the force \(F\) divided by the area \(A\) of the piston, \(P=F/A\). Given this, the observed pressure is just:

\[P = \dfrac{dE}{Adz} \label{Eq3.31} \]

Since the volume decreases when the system is compressed, we see that \(Adz = -dV\). Hence, we can write the pressure as \(P = -dE/dV\).

Of course, the relation \(P = -dE/dV\) is a thermodynamic one, but we need a function of \(x\) that we can average over the ensemble. The most natural choice is:

\[p(x) = -\dfrac{d \mathcal{E} (x)}{dV} \label{Eq3.32} \]

so that \(P = \langle p(x) \rangle\). Setting up the average, we obtain:

\[\begin{align} P &= -\dfrac{C_N}{Q(N, V, T)} \int \dfrac{\partial \mathcal{E}}{\partial V} e^{-\beta \mathcal{E} (x)} \\ &= \dfrac{C_N}{Q(N, V, T)} \dfrac{1}{\beta} \int \dfrac{\partial}{\partial V} e^{-\beta \mathcal{E} (x)} \\ &= \dfrac{kT}{Q(N, V, T} \dfrac{\partial}{\partial V} C_N \int e^{-\beta \mathcal{E} (x)} \\ &= kT \left( \dfrac{\partial \: \text{ln} \: Q(N, V, T)}{\partial V} \right) \end{align} \label{Eq3.33} \]

Ideal Gas in the Canonical Ensemble

Recall that the mechanical energy for an ideal gas is:

\[\mathcal{E} (x) = \sum_{i=1}^N \dfrac{\textbf{p}_i^2}{2m} \label{Eq3.36} \]

where all particles are identical and have mass \(m\). Thus, the expression for the canonical partition function \(Q(N, V, T)\) is:

\[Q(N, V, T) = \dfrac{1}{N!h^{3N}} \int dx \: e^{-\beta \sum_{i=1}^N \textbf{p}_i^2/2m} \nonumber \]

Note that this can be expressed as:

\[Q(N, V, T) = \dfrac{1}{N!h^{3N}}V^N \left[ \int dp \: e^{-\beta p^2/2m} \right]^{3N} \nonumber \]

Evaluating the Gaussian integral gives us the final result immediately:

\[Q(N, V, T) = \dfrac{1}{N!} \left[ \dfrac{V}{h^3} \left( \dfrac{2 \pi m}{\beta} \right)^{3/2} \right]^N \nonumber \]

The expressions for the energy:

\[E = -\dfrac{\partial}{\partial \beta} \: \text{ln} \: Q(N, V, T) \nonumber \]

which gives:

\[E = \dfrac{3}{2}NkT = \dfrac{3}{2}nRT \label{Eq3.37} \]

and pressure:

\[P = kT \left( \dfrac{\partial \: \text{ln} \: Q(N, V, T)}{\partial V} \right) \nonumber \]

giving:

\[P = \dfrac{NkT}{V} = \dfrac{nRT}{V} \label{Eq3.38} \]

which is the ideal gas law.