15.1: Electronically Excited Molecules
- Page ID
- 51115
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)To understand how lasers work we must first describe how a molecule in an excited state can relax back to the ground state because the light emitted by a laser is influenced by these relaxation processes. The two radiative decay pathways for an excited molecule are fluorescence and phosphorescence. Fluorescence differs from phosphorescence in that the energy transition that is responsible for fluorescence does not involve a change in electron spin multiplicity. Thus fluorescence lifetimes are short (10-9 - 10-6 s). In phosphorescence, there is a change in electron spin multiplicity, resulting in a longer lifetime of the excited state (second to minutes). A description of electron spin and the differences between singlet and triplet states will clarify the difference between fluorescence and phosphorescence.
Spin Multiplicity - Singlet and Triplet Excited States
The Pauli Exclusion principle states that two electrons in an atom cannot have the same four quantum numbers (\(n\), \(l\), \(m_l\), \(m_s\)). Therefore, because two electrons can occupy each orbital, these two electrons must have opposite spin states. These opposite spin states are called spin pairing. Because of this spin pairing, most molecules are diamagnetic, and are not attracted or repelled by an external magnetic or electric field. Molecules that contain unpaired electrons (free radicals) do have magnetic moments that are attracted to an external magnetic or electric field.
A molecule is said to be in a singlet state when all the electron spins are paired in the molecular electronic state, and the electronic energy levels do not split when the molecule is exposed to a magnetic field. A doublet state occurs when there is an unpaired electron that gives two possible orientations when exposed to a magnetic field and imparts different energies to the system. A singlet or a triplet state can form when one electron is excited to a higher energy level. In an excited singlet state, the promoted electron retains the spin orientation it had in the ground state (i.e., paired). In a triplet excited state, the promoted electron undergoes a change in spin, and so has the same spin orientation (parallel) to the unpaired electron that remains in the ground state orbital. The difference between the spins of ground singlet, excited singlet, and excited triplet is shown in Figure 15.1.1 . The terms singlet, doublet and triplet are derived using the equation for multiplicity, 2S+1, where S is the total spin angular momentum (sum of all the electron spins). Individual spins are denoted as spin up (s = +1/2) or spin down (s = -1/2). If we were to calculate the multiplicity for the singlet ground state or the singlet excited state, the equation would be
\[2(+1/2 + -1/2)+1 = 2(0)+1 = 1 \nonumber \]
In a similar fashion, the spin multiplicity for the triplet excited state can be calculated as
\[2(+1/2 + +1/2)+1 = 2(1)+1 =3 \nonumber \]
which gives a triplet state as expected.
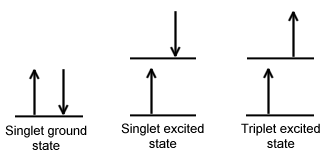
The difference between a molecule in the ground and the triplet excited state is that the molecule is diamagnetic in the ground state and paramagnetic in the triplet excited state. This difference in spin state makes the transition from singlet to triplet (or triplet to singlet) less likely than the singlet-to-singlet transitions. For this reason, the lifetime of the triplet state is longer than the lifetime of the singlet state by a factor of roughly 104 seconds. The transition from ground to excited triplet state has a low probability of occurring, thus these absorption bands are less intense than singlet-singlet state absorption bands. However, an excited triplet state can be populated from an excited singlet state of certain molecules. Jablonski diagrams can be used to explain transitions such as this that occur in photoluminescence molecules.
Jablonski Diagrams
Aleksander Jablonski was a Polish academic who devoted his life to the study of molecular absorbance and emission of light. He developed a graphic representation that shows the possible consequences of applying photons from the visible spectrum of light to a particular molecule. These schematics are referred to as Jablonski diagrams.
A Jablonski diagram is an energy diagram, arranged with energy on a vertical axis. The energy levels can be quantitatively denoted, but most of these diagrams use energy levels schematically. The rest of the diagram is arranged into columns. Every column usually represents a specific spin multiplicity for a particular species. However, some diagrams divide energy levels within the same spin multiplicity into different columns. Within each column, horizontal lines represent eigenstates for that particular molecule. Bold horizontal lines are representations of the limits of electronic energy states. Within each electronic energy state are multiple vibrational energy states that may be coupled with the electronic state. Usually only a portion of these vibrational eigenstates are represented due to the massive number of possible vibrations in a molecule. Each of these vibrational energy states can be subdivided even further into rotational energy levels; however, typical Jablonski diagrams omit such intense levels of detail.
Through the use of straight and wavy lines, these figures show transitions between eigenstates that occur from the exposure of a molecule to a particular wavelength of light. Straight lines show the conversion between a photon of light and the energy of an electron. Wavy lines show nonradiative transitions of electrons. Within a Jablonski diagram several different pathways show how an electron may accept and then dissipate the energy from a photon. Thus, most diagrams start with arrows originating from the ground electronic state and finish with arrows returning to the ground electronic state.
The Jablonski diagram that drawn below is a partial energy diagram that represents the energy of a photoluminescent molecule in its different energy states. The lowest and darkest horizontal line represents the ground-state electronic energy of the molecule which is the singlet state labeled as \(S_o\). At room temperature, a majority of the molecules are in this state. The thicker lines on the left labeled S1, S2 , and S3 represent the excited electronic states for the molecule in the singlet state. The thicker lines on the right labeled T1, T2, and T3 represent excited triplet states.
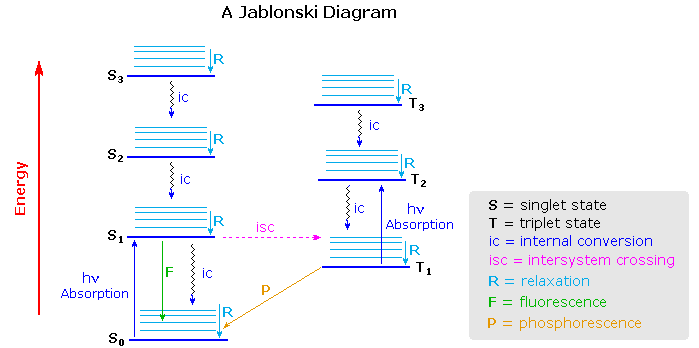
Deactivation Processes
A molecule that is excited can return to the ground state by several combinations of mechanical steps that will be described below and shown in Figure 15.1.2 .The deactivation process of fluorescence and phosphorescence involve an emission of a photon radiation as shown by the straight arrow in Figure 15.1.2 . The wiggly arrows in Figure 15.1.2 are deactivation processes without the use of radiation. The favored deactivation process is the route that is most rapid and spends the least time in the excited state. If the rate constant for relaxation is more favorable in the radiationless path, the fluorescence will be less intense or absent.
Relaxation and Fluorescence
Often, when an excited state species relaxes, giving off a photon, the wavelength of the photon is different from the one that initially led to excitation. When this happens, the photon is invariably red-shifted; its wavelength is longer than the initial one. This situation is called "fluorescence" (Figure \(\PageIndex{3}\)).
How can that be? Isn't energy quantized? How is the molecule suddenly losing some of the energy that the original photon brought with it? This energy discrepancy is related to the Franck-Condon principle from the previous page. When an electron is promoted to an electronic excited state, it often ends up in an excited vibrational state as well (Figure \(\PageIndex{4}\)). Vibrational energy, however, is not exchanged exclusively by means of photons. It can be gained or lost through molecular collisions and heat transfer.
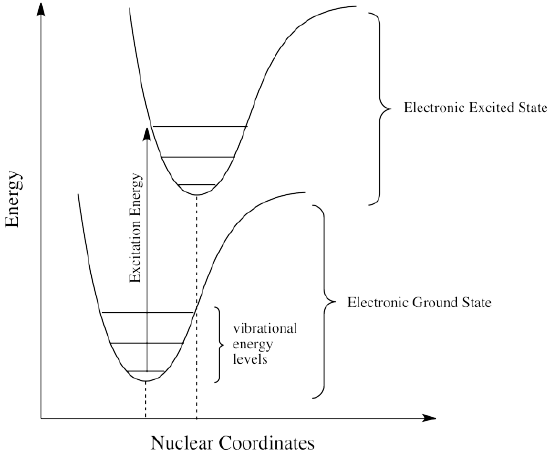
Thus, an excited state molecule with an electron in a high-energy vibrational level within an excited electronic state might simply re-emit a photon of exactly the same wavelength as the one that was absorbed. But the excited electron is much more likely to relax into the lowest vibrational state within the excited electronic state, losing some of that initial excitation energy as heat. When the electron relaxes to this lower vibrational state, the energy gap between this excited state and the ground state is a little smaller. The photon that is emitted upon fluorescence will have lower energy and longer wavelength than a photon emitted from the original, higher vibrational level, excited state. See Figure \(\PageIndex{5}\).
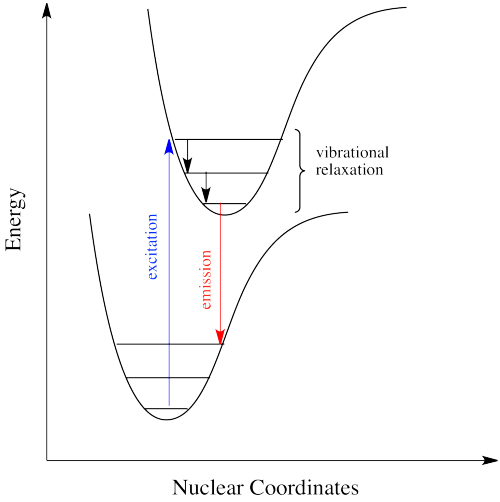
Figure \(\PageIndex{6}\) shows the fluorescence transitions of a hypothetical diatomic molecule in which the equilibrium bond length of the ground state and the first singlet excited state are identical. In this molecule all absorptions involve transitions from the lowest vibrational level of the electronic ground state (\(v^" = 0\)) to various vibrational levels in the excited electronic state. Because vibrational relaxation occurs more rapidly than fluorescence, the fluorescence spectrum is composed of lines showing transitions from the lowest vibrational level of the excited state (\(v^{'} = 0\)) to various vibrational levels in the electronic ground state.
Just how does a molecule undergo vibrational relaxation? Vibrational energy is the energy used to lengthen or shorten bonds, or to widen or squeeze bond angles. Given a big enough molecule, some of this vibrational energy could be transferred into bond lengths and angles further away from the electronic transition. Otherwise, if the molecule is small, it may transfer some of its energy in collisions with other molecules. In molecules, as one molecule drops to a lower vibrational state, the other will hop up to a higher vibrational state with the energy it gains. In Figure \(\PageIndex{7}\) below, the red molecule is in an electronic excited and vibrational state. In a collision, it transfers some of its vibrational energy to the blue molecule.
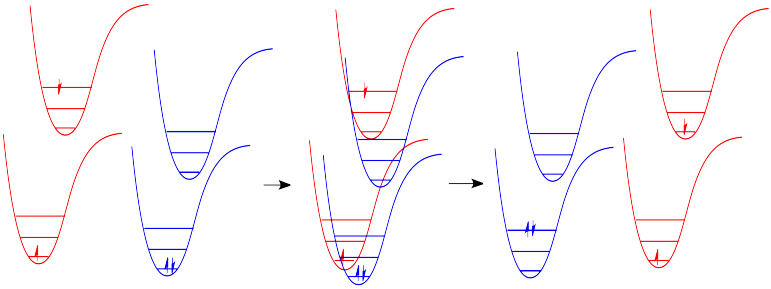
There are many examples of energy being transferred this way in everyday life. In a game of pool, one billiard ball can transfer its energy to another, sending it toward the pocket. Barry Bonds can transfer a considerable amount of energy through his bat into a baseball, sending it out of the park, just as Serena Williams can send a whole lot of energy whizzing back at her sister.
How does the energy of an electronic absorption compare to other processes? To find out, you might consider the excitation of an entire mole of molecules, rather than a single molecule absorbing a single photon. Calculate the energy in kJ/mol for the following transitions.
- absorbance at 180 nm (ultraviolet)
- absorbance at 476 nm (blue)
- absorbance at 645 nm (red)
- Answer
-
One method to carry out this calculation: \( \dfrac{1}{x \text{nm}} \times \dfrac{1 \, \text{nm}}{1x10^{-9} \, \text{m}} \times 6.626 x 10^{-34} \text{Js} \times \dfrac{3.000 x 10^8 \text{m}}{\text{s}} \times \dfrac{6.022 x 10^{23} \text{photons}}{ 1.000 \text{mole}} \times \dfrac{1 \text{kJ}}{1000 \text{J}}\)
- 665.0 kJ/mol
- 251.5 kJ/mol
- 185.6 kJ/mol
How does the energy of an excitation between vibrational states compare to that of an electronic excitation? Typically, infrared absorptions are reported in cm-1, which is simply what it looks like: the reciprocal of the wavelength in cm. Because wavelength and frequency are inversely related, wavenumbers are considered a frequency unit. Calculate the energy in kJ/mol for the following transitions.
- absorbance at 3105 cm-1
- absorbance at 1695 cm-1
- absorbance at 963 cm-1
- Answer
-
One method to carry out this calculation: \( x \text{cm}^{-1} \times \dfrac{100 \, \text{cm}}{1 \, \text{m}} \times 6.626 x 10^{-34} \text{Js} \times \dfrac{3.000 x 10^8 \text{m}}{\text{s}} \times \dfrac{6.022 x 10^{23} \text{photons}}{ 1.000 \text{mole}} \times \dfrac{1 \text{kJ}}{1000 \text{J}}\)
- 37.14 kJ/mol
- 20.27 kJ/mol
- 11.52 kJ/mol
By comparing these answers with those from Exercise \(\PageIndex{1}\), we can see that the energy difference between vibrational states is an order of magnitude less than the energy difference between electronic states.
Internal Conversion
If electrons can get to a lower energy state, and give off a little energy at a time, relaxing to lower and lower vibrational levels, do they need to give off a photon at all? Maybe they can relax all the way down to the ground state via vibrational relaxation. That is certainly the case. Given many vibrational energy levels, and an excited state that is low enough in energy so that some of its lower vibrational levels overlap with some of the higher vibrational levels of the ground state, an electron can relax from an excited electronic state back to the ground state without releasing a photon (Figure \(\PageIndex{8}).
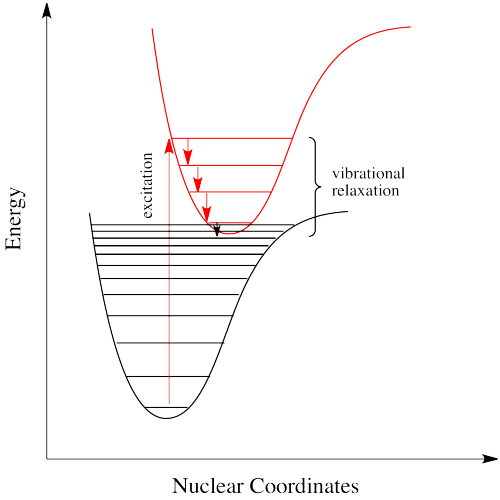
This event is called a "radiationless transition", because it occurs without release of a photon. The electron simply slides over from a low vibrational state of the excited electronic state to a high vibrational state of the electronic ground state. If the electron simply keeps dropping a vibrational level at a time back to the ground state, the process is called "internal conversion".
Internal conversion has an important consequence. Because the absorption of UV and visible light can result in energy transfer into vibrational states, much of the energy that is absorbed from these sources is converted into heat. That can be a good thing if you happen to be a marine iguana trying to warm up in the sun after a plunge in the icy Pacific. It can also be a tricky thing if you are a process chemist trying to scale up a photochemical reaction for commercial production of a pharmaceutical, because you have to make sure the system has adequate cooling available.
Intersystem Crossing
Intersystem crossing is a process that leads to the electron getting caught between the excited state and the ground state. Just as, little by little, vibrational relaxation can lead the electron back onto the ground state energy surface, it can also lead the electron into states that are intermediate in energy in which the spin multiplicity has changed.
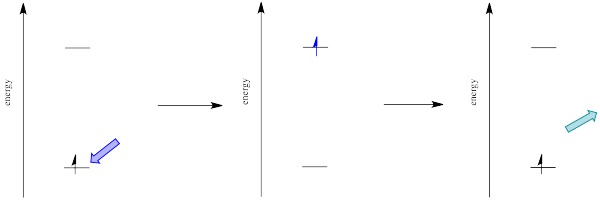
For example, suppose an organic molecule undergoes electronic excitation. Generally, organic molecules have no unpaired electrons. Their ground states are singlet states. According to one of the selection rules for electronic excitation, the excited state must also have no unpaired electrons. In other words, the spin on the electron that gets excited is the same after excitation as it was before excitation.
However, that's not the lowest possible energy state for that electron. When we think about atomic orbital filling, there is a rule that governs the spin on the electrons in degenerate orbitals: in the lowest energy state, spin is maximized (Hund's rule). In other words, when we draw a picture of the valence electron configuration of nitrogen, we show nitrogen's three p electrons each in its own orbital, with their spins parallel.

In Figure \(\PageIndex{9}\), the diagram on the left, with three unpaired electrons, all with parallel spins, shows a nitrogen in the quartet spin state. This is the most stable state. Having one of those spins point the other way would result in a different, higher energy spin state. The diagram on the right shows a different a different spin state, in which one pair of electrons in the p level is spin-paired, one up and one down, even though they are in different p orbitals. That would leave one electron without an opposite partner, so the nitrogen would be in a doublet spin state. The spin state on the left is lower in energy than the state on the right. That's just one of the rules of quantum mechanics (Hund's rule): maximize spin when degenerate orbitals are singly occupied.
A similar argument can be made for a molecule with the triplet state lower in energy than the singlet state, as shown in Figure \(\PageIndex{10}\). Why didn't the electron get excited to the triplet state in the first place? That is a forbidden (unlikely) electronic transition. But sliding down vibrationally onto the triplet state from the singlet excited state is not, because it doesn't involve absorption or emission of a photon.
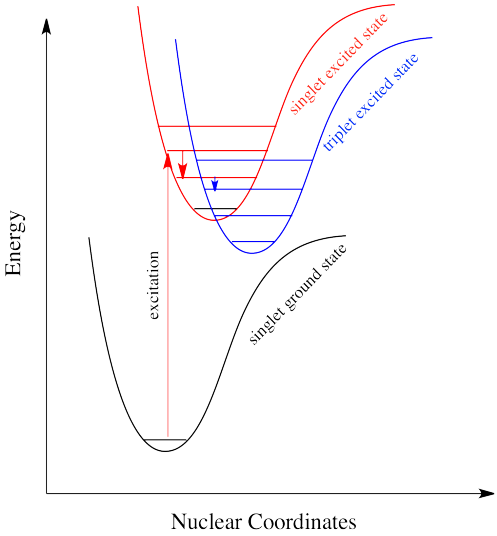
Intersystem crossing can have important consequences in reaction chemistry because it allows access to triplet states that are not normally available in many molecules. Because triplet states feature unpaired electrons, their reactivity is often typified by radical processes. That means an added suite of reactions can be accessed via this process.
Phosphorescence: A Radiationless Transition Followed by Emission
Intersystem crossing is one way a system can end up in a triplet excited state. Even though this state is lower in energy than a singlet excited state, it cannot be accessed directly via electronic excitation because that would violate the spin selection rule (\Delta S=0\). Once intersystem crossing has occurred, the process of reattaining the ground state slows down dramatically. The quick way back to ground state is to emit a photon. But because that would involve a change in spin state, it is not allowed. Realistically speaking, that means it takes a long time. By "a long time", we might mean a few seconds, several minutes, or possibly even hours. Eventually, the electron can drop back down, accompanied by the emission of a photon. This situation is called "phosphorescence" (Figure \(\PageIndex{11}).
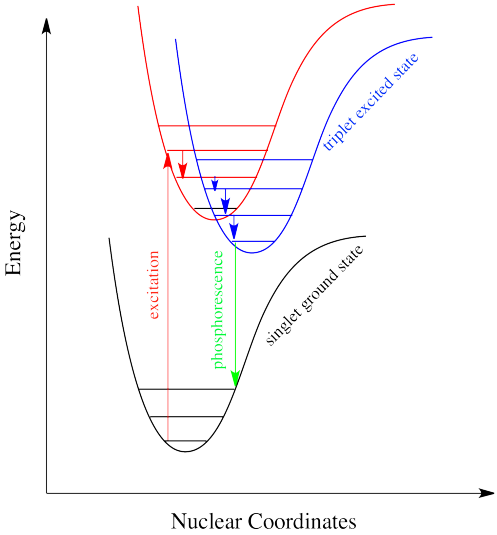
Many plants and animals use phosphorescence as a means of signaling. Molecules that display phosphorescence are also often incorporated into toys and shirts so that they will glow in the dark.
External Conversion
Deactivation of the excited electronic state may also involve the interaction and energy transfer between the excited state and the solvent or solute in a process called external conversion. Low temperature and high viscosity lead to enhanced fluorescence because they reduce the number of collision between molecules, thus slowing down this type of deactivation process.
Absorption and Emission Rates
The table below compares the absorption and emission rates of fluorescence and phosphorescence. The rate of photon absorption is very rapid. Fluorescence emission occurs at a slower rate. Since the triplet to singlet (or reverse) is a forbidden transition, meaning it is less likely to occur than the singlet-to-singlet transition, the rate of triplet to singlet is typically slower. Therefore, phosphorescence emission requires more time than fluorescence.
| Process | Radiative Process? | Transition | Timescale (sec) |
|---|---|---|---|
| Light Absorption (Excitation) | yes | S0 → Sn | ca. 10-15 (instantaneous) |
| Internal Conversion | no | Sn → S1 | 10-14 to 10-11 |
| Vibrational Relaxation | no | Sn* → Sn | 10-12 to 10-10 |
| Intersystem Crossing | no | S1 → T1 | 10-11 to 10-6 |
| Fluorescence | yes | S1 → S0 | 10-9 to 10-6 |
| Phosphorescence | yes | T1 → S0 | 10-3 to 100 |
| Non-Radiative Decay to Ground State (Internal Conversion) | no | S1 → S0 T1 → S0 |
10-7 to 10-5 10-3 to 100 |
References
- D. A. Skoog, et al. "Principles of Instrumental Analysis" 6th Edition, Thomson Brooks/Cole. 2007
- D. C. Harris and M.D. Bertolucci "Symmetry and Spectroscopy, An Introduction to Vibrational and Electronic Spectroscopy" Dover Publications, Inc., New York. 1989.
Contributors and Attributions
Chris P Schaller, Ph.D., (College of Saint Benedict / Saint John's University)
- Diana Wong (UCD)
- Tom Neils (Grand Rapids Community College)

