12.3: Symmetry Operations Define Groups
- Page ID
- 51070
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Now that we have explored some of the properties of symmetry operations and elements and their behavior within point groups, we are ready to introduce the formal mathematical definition of a group.
A mathematical group is defined as a set of elements (\(g_1\), \(g_2\), \(g_3\)...) together with a rule for forming combinations \(g_i\)\(g_j\). The number of elements \(h\) is called the order of the group. For our purposes, the elements are the symmetry operations of a molecule and the rule for combining them is the sequential application of symmetry operations investigated in the previous section. The elements of the group and the rule for combining them must satisfy the following criteria.
- The group must include the identity \(E\), for which \[E g_i= g_i \label{7.1}\] for all the elements of the group.
- The elements must satisfy the group property that the combination of any pair of elements is also an element of the group.
- Each element \(g_i\) must have an inverse \(g_i^{-1}\), which is also an element of the group, such that \[g_i g_i^{-1} = g_i^{-1}g_i = E \label{7.2}\] (e.g. in \(C_{3v}\) the inverse of \(C_3^+\) is \(C_3^-\), the inverse of \((\sigma_v\) is \(\sigma_v\)', the inverse \(g_i^{-1}\) effectively 'undoes’ the effect of the symmetry operation \(g_i\)).
- The rule of combination must be associative i.e. \[(g_i g_j )(g_k) = g_i(g_jg_k) \label{7.3}\]
The above definition does not require the elements to commute, which would require
\[g_i g_k =g_k g_i \label{7.4}\]
As we discovered in the \(C_{3v}\) example above, in many groups the outcome of consecutive application of two symmetry operations depends on the order in which the operations are applied.
Note: Commuting is not a Requirement of Group Elements
Groups for which the elements do not commute are called non-Abelian groups; those for which they elements do commute are Abelian.
Group theory is an important area in mathematics, and luckily for chemists the mathematicians have already done most of the work for us. Along with the formal definition of a group comes a comprehensive mathematical framework that allows us to carry out a rigorous treatment of symmetry in molecular systems and learn about its consequences.
Many problems involving operators or operations (such as those found in quantum mechanics or group theory) may be reformulated in terms of matrices. Any of you who have come across transformation matrices before will know that symmetry operations such as rotations and reflections may be represented by matrices. It turns out that the set of matrices representing the symmetry operations in a group obey all the conditions laid out above in the mathematical definition of a group, and using matrix representations of symmetry operations simplifies carrying out calculations in group theory. Before we learn how to use matrices in group theory, it will probably be helpful to review some basic definitions and properties of matrices.
Group Multiplication
Now we will investigate what happens when we apply two symmetry operations in sequence. As an example, consider the \(NH_3\) molecule, which belongs to the \(C_{3v}\) point group. Consider what happens if we apply a \(C_3\)rotation followed by a \(\sigma_v\) reflection. We write this combined operation \(\sigma_v\)\(C_3\) (when written, symmetry operations operate on the thing directly to their right, just as operators do in quantum mechanics – we therefore have to work backwards from right to left from the notation to get the correct order in which the operators are applied). As we shall soon see, the order in which the operations are applied is important.
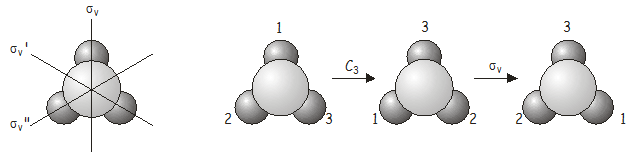
The combined operation \(\sigma_v\)\(C_3\) is equivalent to \(\sigma_v''\), which is also a symmetry operation of the \(C_{3v}\) point group. Now let’s see what happens if we apply the operators in the reverse order i.e. \(C_3\)\(\sigma_v\) (\(\sigma_v\) followed by \(C_3\)).
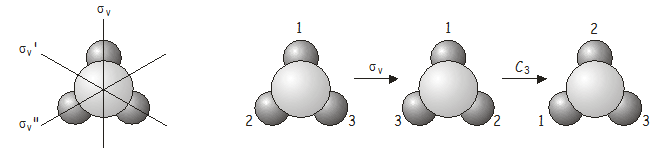
Again, the combined operation \(C_3\)\(\sigma_v\) is equivalent to another operation of the point group, this time \(\sigma_v'\).
There are two important points that are illustrated by this example:
- The order in which two operations are applied is important. For two symmetry operations \(A\) and \(B\), \(AB\) is not necessarily the same as \(BA\), i.e. symmetry operations do not in general commute. In some groups the symmetry elements do commute; such groups are said to be Abelian.
- If two operations from the same point group are applied in sequence, the result will be equivalent to another operation from the point group. Symmetry operations that are related to each other by other symmetry operations of the group are said to belong to the same class. In \(NH_3\), the three mirror planes \(\sigma_v\), \(\sigma_v'\) and \(\sigma_v''\) belong to the same class (related to each other through a \(C_3\) rotation), as do the rotations \(C_3^+\) and \(C_3^-\) (anticlockwise and clockwise rotations about the principal axis, related to each other by a vertical mirror plane
The effects of applying two symmetry operations in sequence within a given point group are summarized in group multiplication tables. As an example, the complete group multiplication table for \(C_{3v}\) using the symmetry operations as defined in the figures above is shown below. The operations written along the first row of the table are carried out first, followed by those written in the first column (note that the table would change if we chose to name \(\sigma_v\), \(\sigma_v'\) and \(\sigma_v''\) in some different order).
\[\begin{array}{l|llllll} C_{3v} & E & C_3^+ & C_3^- & \sigma_v & \sigma_v' & \sigma_v'' \\ \hline E & E & C_3^+ & C_3^- & \sigma_v & \sigma_v' & \sigma_v'' \\ C_3^+ & C_3^+ & C_3^- & E & \sigma_v' & \sigma_v'' & \sigma_v \\ C_3^- & C_3^- & E & C_3^+ & \sigma_v'' & \sigma_v & \sigma_v' \\ \sigma_v & \sigma_v & \sigma_v'' & \sigma_v' & E & C_3^- & C_3^+ \\ \sigma_v' & \sigma_v' & \sigma_v & \sigma_v'' & C_3^+ & E & C_3^- \\ \sigma_v'' & \sigma_v'' & \sigma_v' & \sigma_v & C_3^- & C_3^+ & E \end{array} \label{5.1}\]
Contributors and Attributions
Claire Vallance (University of Oxford)

