Solutions 6
- Page ID
- 47378
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Name: ______________________________
Section: _____________________________
Student ID#:__________________________
S6.1
Consider this acid-catalyzed iodine induced decomposition of hydrogen peroxide (unbalanced equation):
\[H_2O_2 + 3 I^- \rightarrow H_2O + I_3^-\]
The rate was that was experimentally determined to be:
\[rate = k [H_2O_2][I^-][H^+]\]
Which of the following mechanisms would be explain the measured rate law and balanced reaction?
Mechanism A:
\[H_2O_2 + 3 I^- + 2H^+ \rightarrow 2H_2O + I_3^-\]
Mechanism B:
\[H^+ + I^- \rightleftharpoons HI \tag{fast equilibrium}\]
\[H_2O_2 + HI \rightarrow H_2O + HOI \tag{slow}\]
\[HOI+ I^- \rightarrow OH^- + I_2 \tag{fast}\]
\[OH^- + H^+ \rightarrow H_2O \tag{fast}\]
\[I^- +I_2 \rightarrow I_3^- \tag{fast}\]
Mechanism C:
\[H^+ + I^- \rightarrow HI \tag{slow}\]
\[H_2O_2 + HI \rightarrow H_2O + HOI \tag{fast}\]
\[HOI+ I^- \rightarrow OH^- + I_2 \tag{fast}\]
\[OH^- + H^+ \rightarrow H_2O \tag{fast}\]
Mechanism D:
\[ H_2O_2 + H^+ + I^- \rightarrow H_2O + HOI \tag{slow}\]
\[HOI+ I^- \rightarrow OH^- + I_2 \tag{fast}\]
\[I^- +I_2 \rightarrow I_3^- \tag{fast}\]
\[OH^- + H^+ \rightarrow H_2O \tag{fast}\]
To solve this problem we need to compare the rate limiting step of each mechanism to our know rate equation. Mechanism A is incorrect as it involves a sixth order reaction while our rate law is third order. Mechanism B is correct because the rate limiting step involves hydrogen peroxide along with reduced iodine and oxidized hydrogen as they equilibrate fast to form HI. Mechanism C does not work because the rate limiting step does not involve the hydrogen peroxide. Mechanism D is correct though as the rate limiting step matches the rate law.
S6.2
The reaction \[H_{2(g)} + Br_{2(g)} \rightarrow 2HBr_{(g)} \] appears to occur view a multiple step mechanism:
\[Br_{2} \rightleftharpoons 2 Br_{(g )} \tag{fast equilibrium}\]
\[ H_{2(g)} + Br(g) \rightleftharpoons HBr_{(g)} + H_{(g)} \tag{slow}\]
\[H_{(g)} + Br_{(g)} \rightarrow HBr_{(g)} \tag{fast}\]
- What is the role of H(g) in the mechanism: reactant, product, reaction intermediate, or transition state?
- If this mechanism is correct, what is the overall rate law for the reaction?
- Which one of the following reaction diagrams best agrees with the mechanism? Identify all reactants, products, reaction intermediates, and transition states in the selected profile.
a) Reaction Intermediate
b) \(rate = k[H_2][Br_2]\)
c) Diagram B is the correct one. The first corresponds to the fast equilibrium step, the second peak corresponds to the slow step and the third peak corresponds to the final fast step.
S6.3
If the rate of a reaction is quadrupled when the temperature was increased from \(55^o\) C to \(60^o\) C. What is the activation barrier for this reaction?
This problem is the same as problem 5 from HW #4 so I will not repeat the math here, you can look at that solution if you need to.
Here we have \(T_1 = 328 K and T_2 = 333 K\) while \(k_1 = 4*k_2\) that leads to an activation energy of 232 kJ/mol.
S6.4
If the activation energy for a chemical reaction is 65.7 kJ/mol, then how many times faster will the reaction occur at \(50^o\) C than \(0^o\) C?
\[k_1 = A*e^{\frac{657000}{323}{8.314}} = 2.36 x 10^{-11}*A \]
\[k_2 = A*e^{\frac{657000}{273}{8.314}} = 2.66 x 10^{-13}*A \]
\[\frac{k_1}{k_2} = 100\]
S6.5
This reaction is well studied to understand basic mechanisms of gas phase reaction dynamics: \[H_{(g)} + H_{2(g)} \rightarrow H_{2(g)} + H_{(g)}\] A contour plot of the potential energy surface of the collinear collision of \(H\) and \(H_2\) is shown below, where \(r_{AB}\) is the bond length of the reactant \(H_2\) and \(r_{BC}\) is the bond length of the product \(H_2\) .
- Label the transition state.
- Draw a dashed line that indicates the lowest energy path of the reaction
- What is the distance between the \(H\) atom and each hydrogen of the \(H_2\) atom in the transition state? (hint: A drawing of the transition state would probably help)
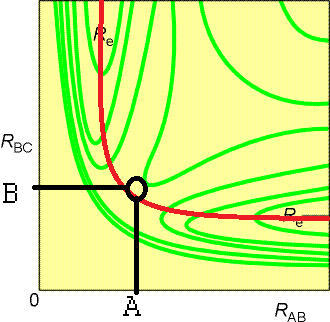
- Black Circle
- Red Line
- H1-H2-H3
Since the collision is collinear and lowest energy path is symmetric the distance from H1 to H2 is A meters and the distance between H1 to H3 is 2A meters.
S6.6
What two factors determine if a single collision will be productive in generating a product in collision theory?
The two factors are whether the collision has enough energy to get over the activation barrier and the steric factors of the molecules involved.
S6.7
Cyclohexane converts between the chair” and “boat” conformations with the enthalpy and entropy of the formation of the activated complex are known to be 31.9 KJ mol-1 and 16.7 J K-1 mol-1, respectively.
- Determine the Gibbs energy of activation and the rate constant for this conversion at room temperature.
- Hypothesize what the structure of the transition state might be.
a) Gibbs energy of the activated complex = enthalpy - temperature * entropy = 31900 J/mol - (16.7 J/Kmol)*(298 K) =
26900 J/mol
b) The activated complex might be flat on one end, a shape halfway between a chair and a boat conformations.

