2015 Exam 1 Solutions
- Page ID
- 120333
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Q1.
The main equation for the photoelectric effect is:
\[KE = h\nu - \phi\tag{1.1}\]
For the lowest energy photon that will kick out an electron we set \(KE = 0\)
\[\dfrac{\phi}{h} = \nu\tag{1.2}\]
\[\dfrac{5.65 eV}{4.14 \times 10^{-15} eVs} = 1.37 \times 10^{15} Hz\tag{1.3}\]
For the second part the energy of the incoming photon is:
\[E = \dfrac{hc}{\lambda}\tag{1.4}\]
\[E = 1.33 \times 10^{-18} J = 8.3 eV\tag{1.5}\]
We substract this energy from the work function to get the kinetic energy of the electron:
\[KE = \dfrac{1}{2}m_ev^2 = 2.65 eV = 4.25 \times 10^{-19}J\tag{1.6}\]
\[v = 966\dfrac{km}{s}\tag{1.7}\]
Q2.
The momentum operator is:
\[\hat{p} = -i\hbar\dfrac{d}{dx}\tag{2.1}\]
An eigenfunction of an operator is a function that returns itself multiplied by a constant when the operator acts upon it. The eigenvalue equations is thus
\[-i\hbar\dfrac{d f(x)}{dx} = P_x f(x) \tag{eigenvalue equation}\]
and \(p_x\) is the eigenvalue (scaler) of the momentum operator, i.e., the linear momentum associated with the eigenstate \(f(x)\)
Looking at A, B, C we can see that \(\dfrac{d}{dx}\) operating on sine squared or cosine returns a different function so they are out. Now let's check for the funciton in A:
\[-i\hbar\dfrac{dAe^{i3x}}{dx} = 3\hbar Ae^{3ix}\tag{2.2}\]
We start with \[Ae^{3ix}\] and end with the same function multiplied by the constant \(3\hbar\) which is the corresponding eigenvalue.
Q3.
For this problem you can run through the integral:
\[\int_{0}^{L/4}\psi_4^*\psi \;dx= \int_{0}^{L/4}{\dfrac{L}{4}} \sin^2{\dfrac{4\pi x}{L}} dx \tag {3.1}\]
Or you can draw out the probability density, given that n = 4 there are three nodes which means four equally spaced bumps there for the probability of the particle being in the first fourth of the box is 25%.
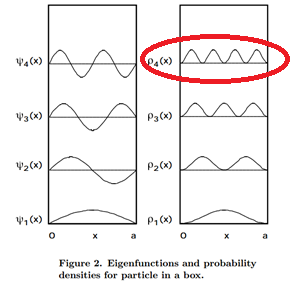
Q4.
For a harmonic oscillator:
\[\nu = 8.963 \times 10^{13}Hz\]
\[2\pi\nu = \sqrt{\dfrac{k}{\mu}} \tag{4.1}\]
\[\mu = \dfrac{m_1 \times m_2}{m_1 + m_2}\tag{4.2}\]
Where \(m_1\) is the mass of hydrogen and \(m_2\) = mass of chlorine
\[k = (2\pi\nu)^2\mu\tag{4.3}\]
\[k = 516.7 \dfrac{Kg}{s}\]
Q5
First we must normalize \(\psi\)
\[\int_{0}^{L} \psi(x)^*\psi(x)dx = 1\tag{5.1}\]
\[A^2\int_{0}^{L}x^2(1-\dfrac{x}{L})^2dx = 1\tag{5.2}\]
\[A = (\dfrac{30}{L^3})^{1/2}\tag{5.3}\]
\[<\hat{x}> = \dfrac{30}{L^3}\int_{0}^{L}x^3(1-\dfrac{x}{L})^2dx = \dfrac{30}{L^3}\int_{0}^{L}x^3(1 - \dfrac{2x}{L} + \dfrac{x^2}{L^2})dx = \dfrac{L}{2}\tag{5.4}\]
\[\langle \hat{x^2} \rangle = \dfrac{30}{L^3}\int_{0}^{L}x^4(1-\dfrac{x}{L})^2dx = \dfrac{30}{L^3}\int_{0}^{L}x^4(1 - \dfrac{2x}{L} + \dfrac{x^2}{L^2})dx = \dfrac{2L^2}{7}\tag{5.5}\]
\[{\sigma^2}_x = \langle \hat{x^2} \rangle - \langle \hat{x} \rangle^2 = \dfrac{2L^2}{7} - \dfrac{L^2}{4} = \dfrac{L^2}{28}\tag{5.6}\]
\[\sigma_x = \dfrac{L}{28^{1/2}}\tag{5.7}\]
Q6.
a) For the \(v=0\) quantum state the wavefunction and mean displacement are:
\[ | \psi_0 \rangle = \left(\dfrac{\alpha}{\pi}\right)^{1/4} e^{ -\alpha x^2/2} \tag{6.1}\]
\[\langle \hat{x} \rangle_0 = \sqrt{ \dfrac{\alpha}{\pi}} \int_{-\infty}^{\infty} xe^{-\alpha x^2}dx = 0\tag{6.2}\]
This integral is equal to zero because we are integrating an odd function over symmetric limits (\(x\) is an odd function while \(e^{x^2}\) is an even function and an even function times an odd function is odd).
For the \(v=1\) quantum the wavefunction and mean displacement are:
\[ | \psi_1 \rangle = \left(\dfrac{\alpha}{\pi}\right)^{1/4} (2\alpha)^{1/2}xe^{-\alpha x^2/2} \tag{6.3}\]
\[\langle \hat{x} \rangle_1 = 2 \sqrt{ \dfrac{\alpha^3}{\pi} } \int_{-\infty}^{\infty} x^3e^{-\alpha x^2}dx = 0\tag{6.4}\]
Again the integral is zero because we are integrating an odd function over symmetric limits.
As they are both zero there is no difference between the mean displacements because both are symmetric around zero.
b) Using the same \(| \psi_0 \rangle\) and \(| \psi_1 \rangle\) from the previous problem the mean displacements squared are:
\[\langle \hat{x}^2 \rangle_0 = \sqrt{ \dfrac{\alpha}{\pi}} \int_{-\infty}^{\infty} x^2e^{-\alpha x^2}dx = \sqrt{ \dfrac{\alpha}{\pi}} \left(\dfrac{1}{2}\right) \left(\dfrac{\pi}{\alpha^3} \right) = \dfrac{1}{2 \alpha}\tag{6.5}\]
\[\langle \hat{x}^2\rangle_1 = 2 \sqrt{ \dfrac{\alpha^3}{\pi}} \int_{-\infty}^{\infty} x^4e^{-\alpha x^2}dx = \dfrac{3}{2 \alpha}\tag{6.6}\]
The difference in the mean displacement squared is due to the probability density of \(| \psi_1 \rangle\) being wider than the probability density of \(| \psi_0 \rangle\) as can be seen on the graphs in the lecture notes.

