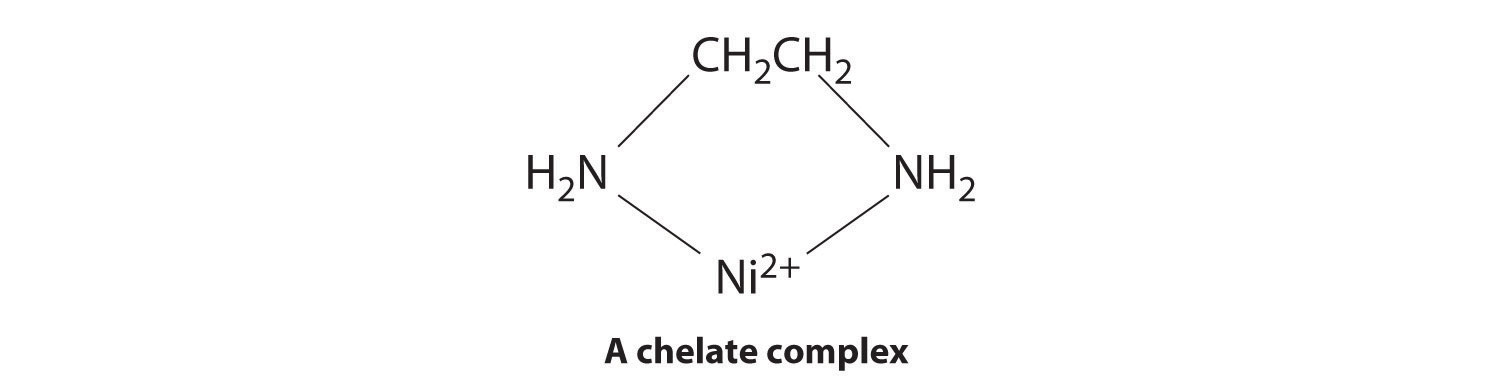
Ligands like chloride, water, and ammonia are said to be monodentate (one-toothed, from the Greek mono, meaning “one,” and the Latin dent-, meaning “tooth”): they are attached to the metal via only a single atom. Ligands can, however, be bidentate (two-toothed, from the Greek di, meaning “two”), tridentate (three-toothed, from the Greek tri, meaning “three”), or, in general, polydentate (many-toothed, from the Greek poly, meaning “many”), indicating that they are attached to the metal at two, three, or several sites, respectively. Ethylenediamine (H2NCH2CH2NH2, often abbreviated as en) and diethylenetriamine (H2NCH2CH2NHCH2CH2NH2, often abbreviated as dien) are examples of a bidentate and a tridentate ligand, respectively, because each nitrogen atom has a lone pair that can be shared with a metal ion. When a bidentate ligand such as ethylenediamine binds to a metal such as Ni2+, a five-membered ring is formed. A metal-containing ring like that shown is called a chelate ring (from the Greek chele, meaning “claw”). Correspondingly, a polydentate ligand is a chelating agent, and complexes that contain polydentate ligands are called chelate complexes.
Experimentally, it is observed that metal complexes of polydentate ligands are significantly more stable than the corresponding complexes of chemically similar monodentate ligands; this increase in stability is called the chelate effect. For example, the complex of Ni2+ with three ethylenediamine ligands, [Ni(en)3]2+, should be chemically similar to the Ni2+ complex with six ammonia ligands, [Ni(NH3)6]2+. In fact, the equilibrium constant for the formation of [Ni(en)3]2+ is almost 10 orders of magnitude larger than the equilibrium constant for the formation of [Ni(NH3)6]2+ (Table E4):
\(\begin{align} & [\mathrm{Ni(H_2O)_6]^{2+}+6NH_3} & \rightleftharpoons \mathrm{[Ni(NH_3)_6]^{2+}+6H_2O(l)} \hspace{3mm} & K_\mathrm f=\mathrm{4\times10^8} \\
& \mathrm{[Ni(H_2O)_6]^{2+}+3en} & \rightleftharpoons \mathrm{[Ni(en)_3]^{2+}+6H_2O(l)} \hspace{3mm} & K_\mathrm f=\mathrm{2\times10^{18}}\end{align} \label{23.10}\)
The formation constants are formulated as
ligand exchange reactions with aqua ligands being displaced by new ligands (\(NH_3\) or \(en\)) in the examples above.
Chelate complexes are more stable than the analogous complexes with monodentate ligands.
The stability of a chelate complex depends on the size of the chelate rings. For ligands with a flexible organic backbone like ethylenediamine, complexes that contain five-membered chelate rings, which have almost no strain, are significantly more stable than complexes with six-membered chelate rings, which are in turn much more stable than complexes with four- or seven-membered rings. For example, the complex of nickel (II) with three ethylenediamine ligands is about 363,000 times more stable than the corresponding nickel (II) complex with trimethylenediamine (H2NCH2CH2CH2NH2, abbreviated as tn):
\(\begin{align} & \mathrm{[Ni(H_2O)_6]^{2+}+3en} & & \rightleftharpoons \mathrm{[Ni(en)_3]^{2+}+6H_2O(l)} & K_\mathrm f=6.76 \times 10^{17} \\ & \mathrm{[Ni(H_2O)_6]^{2+}+3tn} & & \rightleftharpoons \mathrm{[Ni(tn)_3]^{2+}+6H_2O(l)} & K_\mathrm f=1.86 \times 10^{12}\end{align} \label{23.11}\)
*The above measurements were done in a solution of ionic strength 0.15 at 25º C.
Example \(\PageIndex{1}\)
Arrange [Cr(en)3]3+, [CrCl6]3−, [CrF6]3−, and [Cr(NH3)6]3+ in order of increasing stability.
Given: four Cr(III) complexes
Asked for: relative stabilities
Strategy:
A Determine the relative basicity of the ligands to identify the most stable complexes.
B Decide whether any complexes are further stabilized by a chelate effect and arrange the complexes in order of increasing stability.
Solution
A The metal ion is the same in each case: Cr3+. Consequently, we must focus on the properties of the ligands to determine the stabilities of the complexes. Because the stability of a metal complex increases as the basicity of the ligands increases, we need to determine the relative basicity of the four ligands. Our earlier discussion of acid–base properties suggests that ammonia and ethylenediamine, with nitrogen donor atoms, are the most basic ligands. The fluoride ion is a stronger base (it has a higher charge-to-radius ratio) than chloride, so the order of stability expected due to ligand basicity is
[CrCl6]3− < [CrF6]3− < [Cr(NH3)6]3+ ≈ [Cr(en)3]3+.
B Because of the chelate effect, we expect ethylenediamine to form a stronger complex with Cr3+ than ammonia. Consequently, the likely order of increasing stability is
[CrCl6]3− < [CrF6]3− < [Cr(NH3)6]3+ < [Cr(en)3]3+.
Exercise \(\PageIndex{1}\)
Arrange [Co(NH3)6]3+, [CoF6]3−, and [Co(en)3]3+ in order of decreasing stability.
Answer: [Co(en)3]3+ > [Co(NH3)6]3+ > [CoF6]3−
The Chelate Effect
The chelate effect can be seen by comparing the reaction of a chelating ligand and a metal ion with the corresponding reaction involving comparable monodentate ligands. For example, comparison of the binding of 2,2'-bipyridine with pyridine or 1,2-diaminoethane (ethylenediamine=en) with ammonia. It has been known for many years that a comparison of this type always shows that the complex resulting from coordination with the chelating ligand is much more thermodynamically stable. This can be seen by looking at the values for adding two monodentates compared with adding one bidentate, or adding four monodentates compared to two bidentates, or adding six monodentates compared to three bidentates.
The Chelate Effect is that complexes resulting from coordination with the chelating ligand is much more thermodynamically stable than complexes with non-chelating ligands.
A number of points should be highlighted from the formation constants in Table E4. In Table \(\PageIndex{1}\), it can be seen that the ΔH° values for the formation steps are almost identical, that is, heat is evolved to about the same extent whether forming a complex involving monodentate ligands or bidentate ligands. What is seen to vary significantly is the ΔS° term which changes from negative (unfavorable) to positive (favorable). Note as well that there is a dramatic increase in the size of the ΔS° term for adding two compared to adding four monodentate ligands. (-5 to -35 JK-1mol-1). What does this imply, if we consider ΔS° to give a measure of disorder?
In the case of complex formation of Ni2+ with ammonia or 1,2-diaminoethane, by rewriting the equilibria, the following equations are produced.
Using the equilibrium constant for the reaction (3 above) where the three bidentate ligands replace the six monodentateligands, we find that at a temperature of 25° C:
\[\Delta G^° = -2.303 \, RT \, \log_{10} K \nonumber \]
\[= -2.303 \,RT \,(18.28 - 8.61) \nonumber \]
\[= -54 \text{ kJ mol}^{-1} \nonumber \]
Based on measurements made over a range of temperatures, it is possible to break down the \(\Delta G^°\) term into the enthalpy and entropy components.
\[\Delta G^° = \Delta H^° - T \Delta S^° \nonumber \]
The result is that: \(\Delta H^° = -29 kJ mol^{-1}\)
- TΔS° = -25 kJ mol-1
and at 25C (298K)
ΔS° = +88 J K-1 mol-1
For many years, these numbers have been incorrectly recorded in textbooks. For example, the third edition of "Basic Inorganic Chemistry" by F.A. Cotton, G. Wilkinson and P.L. Gaus, John Wiley & Sons, Inc, 1995, on page 186 gives the values as:
ΔG° = -67 kJ mol-1
ΔH° = -12 kJ mol-1
-TΔS° = -55 kJ mol-1
The conclusion they drew from these incorrect numbers was that the chelate effect was essentially an entropy effect, since the TΔS° contribution was nearly 5 times bigger than ΔH°.
In fact, the breakdown of the ΔG° into ΔH° and TΔS° shows that the two terms are nearly equal (-29 and -25 kJ mol-1, respectively) with the ΔH° term a little bigger! The entropy term found is still much larger than for reactions involving a non-chelating ligand substitution at a metal ion. How can we explain this enhanced contribution from entropy? One explanation is to count the number of species on the left and right hand side of the equation above.
It will be seen that on the left-hand-side there are 4 species, whereas on the right-hand-side there are 7 species, that is a net gain of 3 species occurs as the reaction proceeds. This can account for the increase in entropy since it represents an increase in the disorder of the system. An alternative view comes from trying to understand how the reactions might proceed. To form a complex with 6 monodentates requires 6 separate favorable collisions between the metal ion and the ligand molecules. To form the tris-bidentate metal complex requires an initial collision for the first ligand to attach by one arm but remember that the other arm is always going to be nearby and only requires a rotation of the other end to enable the ligand to form the chelate ring.
If you consider dissociation steps, then when a monodentate group is displaced, it is lost into the bulk of the solution. On the other hand, if one end of a bidentate group is displaced the other arm is still attached and it is only a matter of the arm rotating around and it can be reattached again. Both conditions favor the formation of the complex with bidentate groups rather than monodentate groups.



