5.3: Enthalpy

Skills to Develop

• To know the key features of a state function.
• To use Hess’s law and thermochemical cycles to calculate enthalpy changes of chemical reactions.

To study the flow of energy during a chemical reaction, we need to distinguish between a system, the small, well-defined part of the universe in which we are interested (such as a chemical reaction), and its surroundings, the rest of the universe, including the container in which the reaction is carried out (Figure 5.3.1). In the discussion that follows, the mixture of chemical substances that undergoes a reaction is always the system, and the flow of heat can be from the system to the surroundings or vice versa.

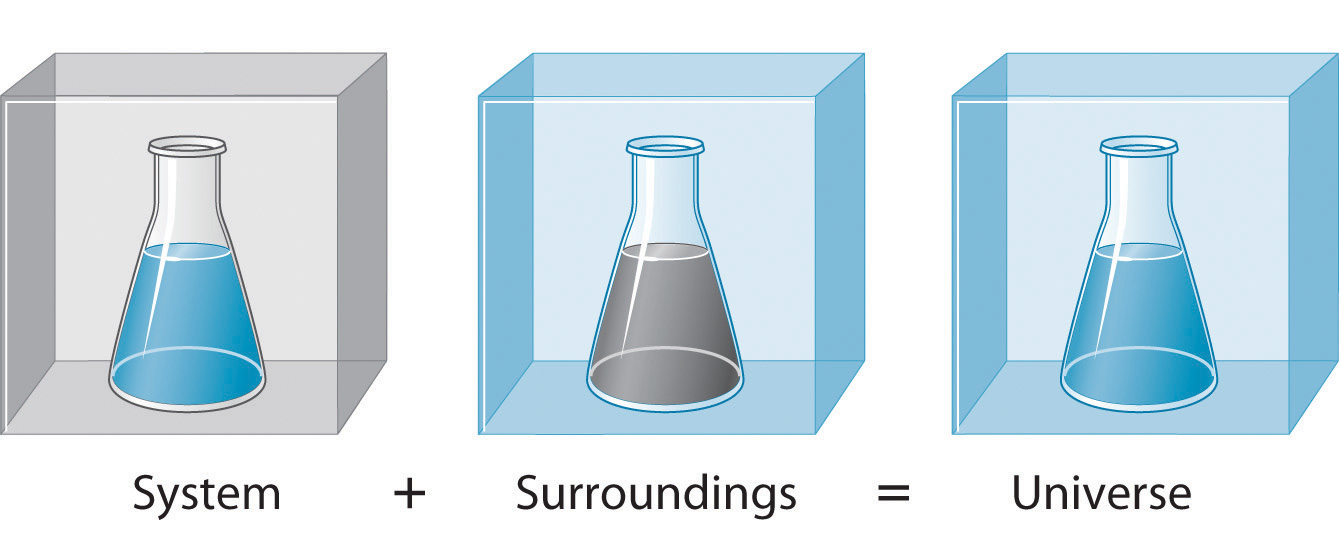
Figure 5.3.1. A System and Its SurroundingsThe system is that part of the universe we are interested in studying, such as a chemical reaction inside a flask. The surroundings are the rest of the universe, including the container in which the reaction is carried out.

Three kinds of systems are important in chemistry. An open system can exchange both matter and energy with its surroundings. A pot of boiling water is an open system because a burner supplies energy in the form of heat, and matter in the form of water vapor is lost as the water boils. A closed system can exchange energy but not matter with its surroundings. The sealed pouch of a ready-made dinner that is dropped into a pot of boiling water is a closed system because thermal energy is transferred to the system from the boiling water but no matter is exchanged (unless the pouch leaks, in which case it is no longer a closed system). An isolated system exchanges neither energy nor matter with the surroundings. Energy is always exchanged between a system and its surroundings, although this process may take place very slowly. A truly isolated system does not actually exist. An insulated thermos containing hot coffee approximates an isolated system, but eventually the coffee cools as heat is transferred to the surroundings. In all cases, the amount of heat lost by a system is equal to the amount of heat gained by its surroundings and vice versa. That is, the total energy of a system plus its surroundings is constant, which must be true if energy is conserved.

The state of a system is a complete description of a system at a given time, including its temperature and pressure, the amount of matter it contains, its chemical composition, and the physical state of the matter. A state function is a property of a system whose magnitude depends on only the present state of the system, not its previous history. Temperature, pressure, volume, and potential energy are all state functions. The temperature of an oven, for example, is independent of however many steps it may have taken for it to reach that temperature. Similarly, the pressure in a tire is independent of how often air is pumped into the tire for it to reach that pressure, as is the final volume of air in the tire. Heat and work, on the other hand, are not state functions because they are path dependent. For example, a car sitting on the top level of a parking garage has the same potential energy whether it was lifted by a crane, set there by a helicopter, driven up, or pushed up by a group of students (Figure 5.3.2). The amount of work expended to get it there, however, can differ greatly depending on the path chosen. If the students decided to carry the car to the top of the ramp, they would perform a great deal more work than if they simply pushed the car up the ramp (unless, of course, they neglected to release the parking brake, in which case the work expended would increase substantially!). The potential energy of the car is the same, however, no matter which path they choose.

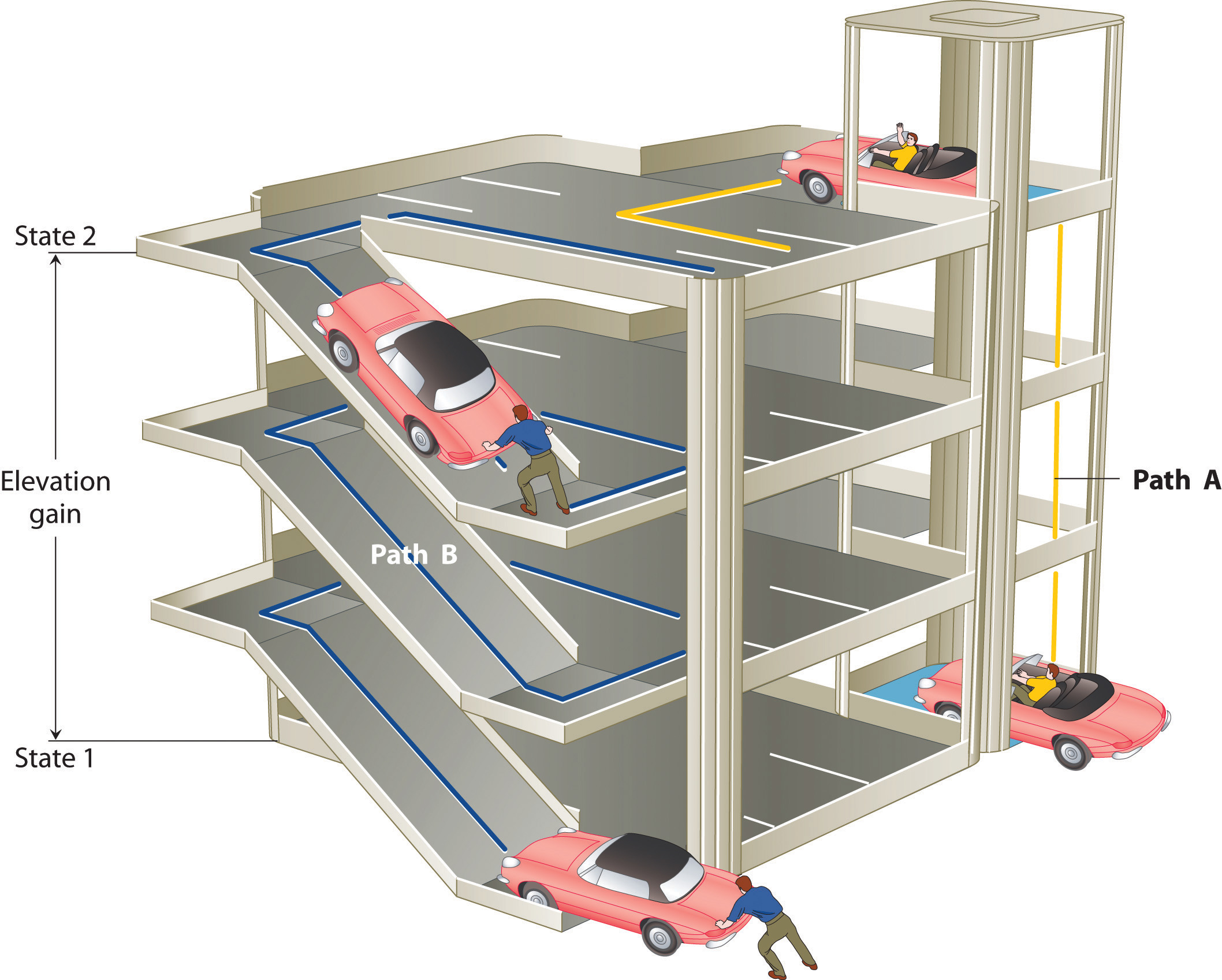
Figure 5.3.2 Elevation as an Example of a State Function. The change in elevation between state 1 (at the bottom of the parking garage) and state 2 (at the top level of the parking garage) is the same for both paths A and B; it does not depend on which path is taken from the bottom to the top. In contrast, the distance traveled and the work needed to reach the top do depend on which path is taken. Elevation is a state function, but distance and work are not state functions.

Direction of Heat Flow

The reaction of powdered aluminum with iron(III) oxide, known as the thermite reaction, generates an enormous amount of heat—enough, in fact, to melt steel (see chapter opening image). The balanced chemical equation for the reaction is as follows:

\[ 2Al(s) + Fe_2O_3(s) \rightarrow 2Fe(s) + Al_2O_3(s) \tag{5.3.1}\]

We can also write this chemical equation as

\[2Al(s) + Fe_2O_3(s) \rightarrow 2Fe(s) + Al_2O_3(s) + \text{heat} \tag{5.3.2}\]

to indicate that heat is one of the products. Chemical equations in which heat is shown as either a reactant or a product are called thermochemical equations. In this reaction, the system consists of aluminum, iron, and oxygen atoms; everything else, including the container, makes up the surroundings. During the reaction, so much heat is produced that the iron liquefies. Eventually, the system cools; the iron solidifies as heat is transferred to the surroundings. A process in which heat (q) is transferred from a system to its surroundings is described as exothermic. By convention, q < 0 for an exothermic reaction.

When you hold an ice cube in your hand, heat from the surroundings (including your hand) is transferred to the system (the ice), causing the ice to melt and your hand to become cold. We can describe this process by the following thermochemical equation:

\[ heat + H_2O(s) \rightarrow H2O(l) \tag{5.3.3}\]

When heat is transferred to a system from its surroundings, the process is endothermic. By convention, \(q > 0\) for an endothermic reaction.

Summary

• Enthalpy is a state function whose change indicates the amount of heat transferred from a system to its surroundings or vice versa, at constant pressure.

In chemistry, the small part of the universe that we are studying is the system, and the rest of the universe is the surroundings. Open systems can exchange both matter and energy with their surroundings, closed systems can exchange energy but not matter with their surroundings, and isolated systems can exchange neither matter nor energy with their surroundings. A state function is a property of a system that depends on only its present state, not its history. A reaction or process in which heat is transferred from a system to its surroundings is exothermic. A reaction or process in which heat is transferred to a system from its surroundings is endothermic.