11.2: Combined gas law
- Page ID
- 369587
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Learn and apply the combined gas law.
- Understand the relationship between PV, VT, and PT
- Solve for Pressure, Volume, or Temperature of a gas system using the Combined Gas Law
Each day, hundreds of weather balloons are launched. Made of a synthetic rubber and carrying a box of instruments, each helium-filled balloon rises up into the sky. As a balloon gains altitude, the atmospheric pressure becomes less and the balloon expands. At some point the balloon bursts due to the expansion; the instruments drop (aided by a parachute) to be retrieved and studied for information about the weather.
Boyle's Law
Robert Boyle (1627-1691), an English chemist, is widely considered to be one of the founders of the modern experimental science of chemistry. He discovered that doubling the pressure of an enclosed sample of gas, while keeping its temperature constant, caused the volume of the gas to be reduced by half. Boyle's law states that the volume of a given mass of gas varies inversely with the pressure when the temperature is kept constant. An inverse relationship is described in this way. As one variable increases in value, the other variable decreases.
Physically, what is happening? The gas molecules are moving and are a certain distance apart from one another. An increase in pressure pushes the molecules closer together, reducing the volume. If the pressure is decreased, the gases are free to move about in a larger volume.
Mathematically, Boyle's law can be expressed by the equation:
\[P \times V = k\]
The \(k\) is a constant for a given sample of gas and depends only on the mass of the gas and the temperature.
Boyle's Law can be used to compare changing conditions for a gas. We use \(P_1\) and \(V_1\) to stand for the initial pressure and initial volume of a gas. After a change has been made, \(P_2\) and \(V_2\) stand for the final pressure and volume. The mathematical relationship of Boyle's Law becomes:
\[P_1 \times V_1 = P_2 \times V_2\]
This equation can be used to calculate any one of the four quantities if the other three are known.
Freshly-baked bread is light and fluffy as a result of the action of yeast on sugar. The yeast converts the sugar to carbon dioxide, which at high temperatures causes the dough to expand. The end result is an enjoyable treat, especially when covered with melted butter.
Charles's Law
French physicist Jacques Charles (1746-1823) studied the effect of temperature on the volume of a gas at constant pressure. Charles's Law states that the volume of a given mass of gas varies directly with the absolute temperature of the gas when pressure is kept constant. The absolute temperature is temperature measured with the Kelvin scale. The Kelvin scale must be used because zero on the Kelvin scale corresponds to a complete stoppage of molecular motion.
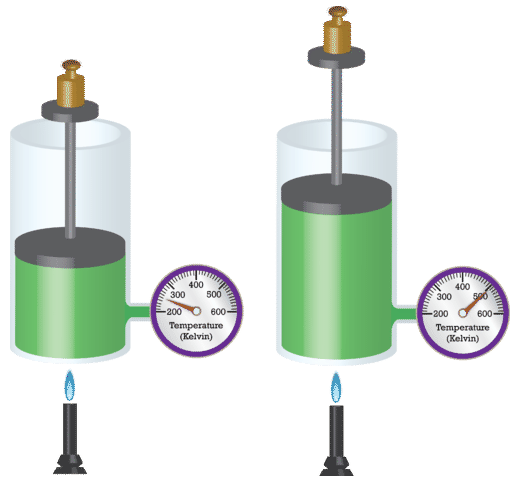
Mathematically, the direct relationship of Charles's Law can be represented by the following equation:
\[\frac{V}{T} = k\]
As with Boyle's Law, \(k\) is constant only for a given gas sample.
Charles's Law can also be used to compare changing conditions for a gas. Now we use \(V_1\) and \(T_1\) to stand for the initial volume and temperature of a gas, while \(V_2\) and \(T_2\) stand for the final volume and temperature. The mathematical relationship of Charles's Law becomes:
\[\frac{V_1}{T_1} = \frac{V_2}{T_2}\]
This equation can be used to calculate any one of the four quantities if the other three are known. The direct relationship will only hold if the temperatures are expressed in Kelvin. Temperatures in Celsius will not work. Recall the relationship that \(\text{K} = \: ^\text{o} \text{C} + 273\).
Propane tanks are widely used with barbeque grills. However, it's not fun to find out half-way through grilling that you've run out of gas. You can buy gauges that measure the pressure inside the tank to see how much is left. The gauge measures pressure and will register a higher pressure on a hot day than it will on a cold day. So, you need to take the air temperature into account when you decide whether or not to refill the tank before your next cook-out.
Gay-Lussac's Law
When the temperature of a sample of gas in a rigid container is increased, the pressure of the gas increases as well. The increase in kinetic energy results in the molecules of gas striking the walls of the container with more force, resulting in a greater pressure. The French chemist Joseph Gay-Lussac (1778-1850) discovered the relationship between the pressure of a gas and its absolute temperature. Gay-Lussac's Law states that the pressure of a given mass of gas varies directly with the absolute temperature of the gas, when the volume is kept constant. Gay-Lussac's Law is very similar to Charles's Law, with the only difference being the type of container. Whereas the container in a Charles's Law experiment is flexible, it is rigid in a Gay-Lussac's Law experiment.

The mathematical expressions for Gay-Lussac's Law are likewise similar to those of Charles's Law:
\[\frac{P}{T} \: \: \: \text{and} \: \: \: \frac{P_1}{T_1} = \frac{P_2}{T_2}\]
A graph of pressure vs. temperature also illustrates a direct relationship. As a gas is cooled at constant volume, its pressure continually decreases until the gas condenses to a liquid.
The modern refrigerator takes advantage of the gas laws to remove heat from a system. Compressed gas in the coils is allowed to expand. This expansion lowers the temperature of the gas and transfers heat energy from the material in the refrigerator to the gas. As the gas is pumped through the coils, the pressure on the gas compresses it and raises the gas temperature. This heat is then dissipated through the coils into the outside air. As the compressed gas is pumped through the system again, the process repeats itself.
Combined Gas Law
To this point, we have examined the relationships between any two of the variables of \(P\), \(V\), and \(T\), while the third variable is held constant. However, situations do arise where all three variables change. The combined gas law expresses the relationship between the pressure, volume, and absolute temperature of a fixed amount of gas. For a combined gas law problem, only the amount of gas is held constant.
\[\frac{P \times V}{T} = k \: \: \: \text{and} \: \: \: \frac{P_1 \times V_1}{T_1} = \frac{P_2 \times V_2}{T_2}\]
\(2.00 \: \text{L}\) of a gas at \(35^\text{o} \text{C}\) and \(0.833 \: \text{atm}\) is brought to standard temperature and pressure (STP). What will be the new gas volume?
Solution
Step 1: List the known quantities and plan the problem.
Known
- \(P_1 = 0.833 \: \text{atm}\)
- \(V_1 = 2.00 \: \text{L}\)
- \(T_1 = 35^\text{o} \text{C} = 308 \: \text{K}\)
- \(P_2 = 1.00 \: \text{atm}\)
- \(T_2 = 0^\text{o} \text{C} = 273 \: \text{K}\)
Unknown
Use the combined gas law to solve for the unknown volume \(\left( V_2 \right)\). STP is \(273 \: \text{K}\) and \(1 \: \text{atm}\). The temperatures have been converted to Kelvin.
Step 2: Solve.
First, rearrange the equation algebraically to solve for \(V_2\).
\[V_2 = \frac{P_1 \times V_1 \times T_2}{P_2 \times T_1}\]
Now substitute the known quantities into the equation and solve.
\[V_2 = \frac{0.833 \: \text{atm} \times 2.00 \: \text{L} \times 273 \: \text{K}}{1.00 \: \text{atm} \times 308 \: \text{K}} = 1.48 \: \text{L}\]
Step 3: Think about your result.
Both the increase in pressure and the decrease in temperature cause the volume of the gas sample to decrease. Since both changes are relatively small, the volume does not decrease dramatically.
It may seem challenging to remember all the different gas laws introduced so far. Fortunately, Boyle's, Charles's, and Gay-Lussac's laws can all be easily derived from the combined gas law. For example, consider a situation where a change occurs in the volume and pressure of a gas while the temperature is being held constant. In that case, it can be said that \(T_1 = T_2\). Look at the combined gas law and cancel the \(T\) variable out from both sides of the equation. What is left over is Boyle's Law: \(P_1 \times V_1 = P_2 \times V_2\). Likewise, if the pressure is constant, then \(P_1 = P_2\) and cancelling \(P\) out of the equation leaves Charles's Law. If the volume is constant, then \(V_1 = V_2\) and cancelling \(V\) out of the equation leaves Gay-Lussac's Law.
Key Takeaway
\(\frac{P_1V_1}{T_1} = \frac{P_2V_2}{T_2}\)

