7.2: The Nature of Matter
- Page ID
- 33906
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Skills to Develop
-
To understand the wave–particle duality of matter.
Einstein’s photons of light were individual packets of energy having many of the characteristics of particles. Recall that the collision of an electron (a particle) with a sufficiently energetic photon can eject a photoelectron from the surface of a metal. Any excess energy is transferred to the electron and is converted to the kinetic energy of the ejected electron. Einstein’s hypothesis that energy is concentrated in localized bundles, however, was in sharp contrast to the classical notion that energy is spread out uniformly in a wave. We now describe Einstein’s theory of the relationship between energy and mass, a theory that others built on to develop our current model of the atom.
The Wave Character of Matter
Einstein initially assumed that photons had zero mass, which made them a peculiar sort of particle indeed. In 1905, however, he published his special theory of relativity, which related energy and mass according to the following equation:
\[ E=h\nu=h\dfrac{c}{\lambda }=mc^{2} \tag{7.2.1} \]
According to this theory, a photon of wavelength λ and frequency ν has a nonzero mass, which is given as follows:
\[ m=\dfrac{E}{c^{2}}=\dfrac{h\nu }{c^{2}}=\dfrac{h}{\lambda c} \tag{7.2.2}\]
That is, light, which had always been regarded as a wave, also has properties typical of particles, a condition known as wave–particle duality (a principle that matter and energy have properties typical of both waves and particles). Depending on conditions, light could be viewed as either a wave or a particle.
In 1922, the American physicist Arthur Compton (1892–1962) reported the results of experiments involving the collision of x-rays and electrons that supported the particle nature of light. At about the same time, a young French physics student, Louis de Broglie (1892–1972), began to wonder whether the converse was true: Could particles exhibit the properties of waves? In his PhD dissertation submitted to the Sorbonne in 1924, de Broglie proposed that a particle such as an electron could be described by a wave whose wavelength is given by
\[\lambda =\dfrac{h}{mv} \tag{7.2.3}\]
where
- is Planck’s constant,
- m is the mass of the particle, and
- v is the velocity of the particle.
This revolutionary idea was quickly confirmed by American physicists Clinton Davisson (1881–1958) and Lester Germer (1896–1971), who showed that beams of electrons, regarded as particles, were diffracted by a sodium chloride crystal in the same manner as x-rays, which were regarded as waves. It was proven experimentally that electrons do exhibit the properties of waves. For his work, de Broglie received the Nobel Prize in Physics in 1929.
If particles exhibit the properties of waves, why had no one observed them before? The answer lies in the numerator of de Broglie’s equation, which is an extremely small number. As you will calculate in Example 7.2.1, Planck’s constant (6.63 × 10−34 J•s) is so small that the wavelength of a particle with a large mass is too short (less than the diameter of an atomic nucleus) to be noticeable.
Example 7.2.1
Calculate the wavelength of a baseball, which has a mass of 149 g and a speed of 100 mi/h.
Given: mass and speed of object
Asked for: wavelength
Strategy:
- Convert the speed of the baseball to the appropriate SI units: meters per second.
- Substitute values into Equation 7.2.3 and solve for the wavelength.
Solution:
The wavelength of a particle is given by λ = h/mv. We know that m = 0.149 kg, so all we need to find is the speed of the baseball:
\( v=\left ( \dfrac{100\; \cancel{mi}}{\cancel{h}} \right )\left ( \dfrac{1\; \cancel{h}}{60\; \cancel{min}} \right )\left ( \dfrac{1.609\; \cancel{km}}{\cancel{mi}} \right )\left ( \dfrac{1000\; m}{\cancel{km}} \right ) \)
B Recall that the joule is a derived unit, whose units are (kg•m2)/s2. Thus the wavelength of the baseball is
\[ \lambda =\dfrac{6.626\times 10^{-34}\; J\cdot s}{\left ( 0.149\; kg \right )\left ( 44.69\; m\cdot s \right )}= \dfrac{6.626\times 10^{-34}\; \cancel{kg}\cdot m{^\cancel{2}\cdot \cancel{s}{\cancel{^{-2}}\cdot \cancel{s}}}}{\left ( 0.149\; \cancel{kg} \right )\left ( 44.69\; \cancel{m}\cdot \cancel{s^{-1}} \right )}=9.95\times 10^{-35}\; m \]
(You should verify that the units cancel to give the wavelength in meters.) Given that the diameter of the nucleus of an atom is approximately 10−14 m, the wavelength of the baseball is almost unimaginably small.
Exercise 7.2.1
Calculate the wavelength of a neutron that is moving at 3.00 × 103 m/s.
Answer: 1.32 Å, or 132 pm
As you calculated in Example 7.2.1, objects such as a baseball or a neutron have such short wavelengths that they are best regarded primarily as particles. In contrast, objects with very small masses (such as photons) have large wavelengths and can be viewed primarily as waves. Objects with intermediate masses, such as electrons, exhibit the properties of both particles and waves. Although we still usually think of electrons as particles, the wave nature of electrons is employed in an electron microscope, which has revealed most of what we know about the microscopic structure of living organisms and materials. Because the wavelength of an electron beam is much shorter than the wavelength of a beam of visible light, this instrument can resolve smaller details than a light microscope can (Figure 7.2.1).
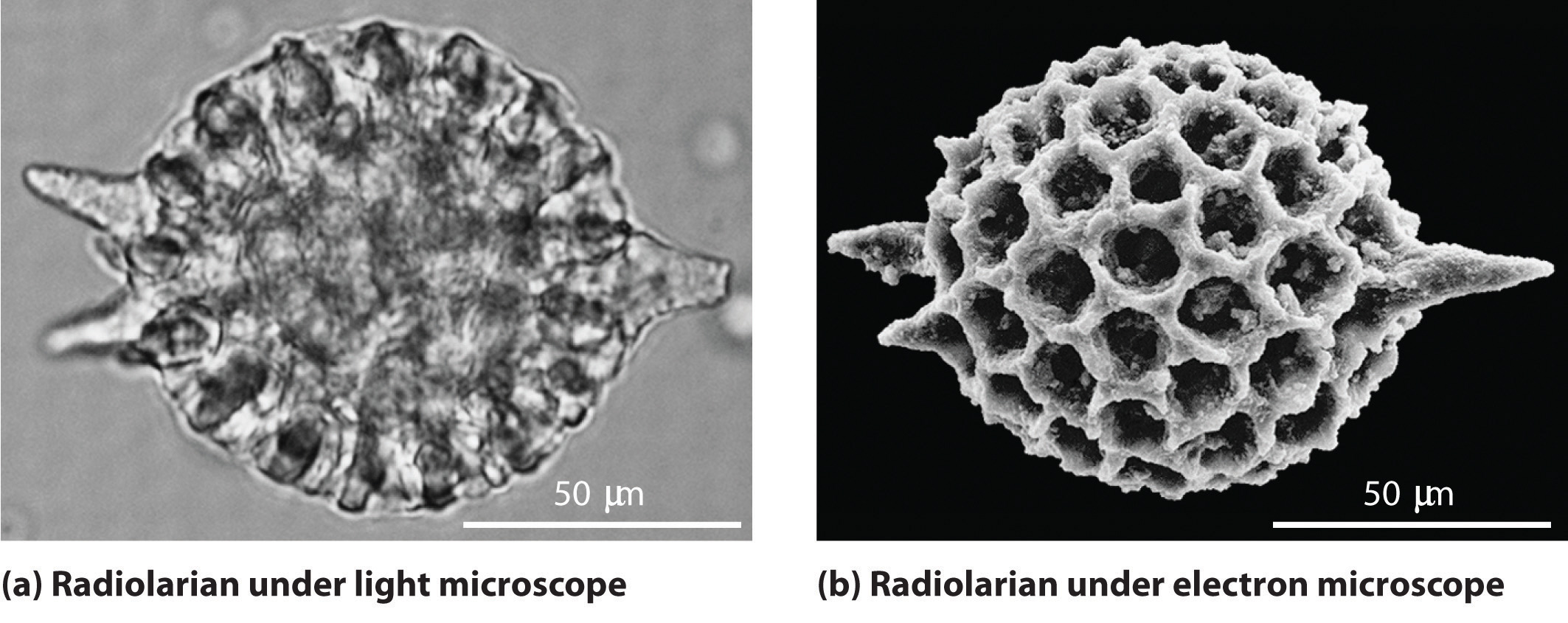
Figure 7.2.1 A Comparison of Images Obtained Using a Light Microscope and an Electron Microscope. Because of their shorter wavelength, high-energy electrons have a higher resolving power than visible light. Consequently, an electron microscope (b) is able to resolve finer details than a light microscope (a). (Radiolaria, which are shown here, are unicellular planktonic organisms.)
Videos and Examples
- de Broglie Waves - Sixty Symbols - a bit of history and explanation (as well as wave particle duality can be explained)
- Calculating the wavelength of a proton - Josh Samson
- Calculating the wavelength of a small car - Prof. Heath
- What is the Uncertainty Principle? - Minute Physics
- AP Chem Heisenberg Uncertainty Principle - Mind Bite
- deBroglie Example - about education
- Heisenberg uncertainty principle quiz worked out - C Craig
- Quantum Chemistry - Ohio State
- Quantum Chemistry Quizzes - mhe education
- AP Chemistry Chapter 7 Review - Science Geek
Answers for these quizzes are included.
Summary
- An electron possesses both particle and wave properties.
The modern model for the electronic structure of the atom is based on recognizing that an electron possesses particle and wave properties, the so-called wave–particle duality. Louis de Broglie showed that the wavelength of a particle is equal to Planck’s constant divided by the mass times the velocity of the particle.
\[\lambda =\dfrac{h}{mv} \tag{7.2.3}\]
The electron in Bohr’s circular orbits could thus be described as a standing wave, one that does not move through space. Standing waves are familiar from music: the lowest-energy standing wave is the fundamental vibration, and higher-energy vibrations are overtones and have successively more nodes, points where the amplitude of the wave is always zero. Werner Heisenberg’s uncertainty principle states that it is impossible to precisely describe both the location and the speed of particles that exhibit wavelike behavior.
\[ \left ( \Delta x \right )\left ( \Delta \left [ mv \right ] \right )\geqslant \dfrac{h}{4\pi } \tag{7.2.7} \]
Contributors
Modified by Joshua Halpern (Howard University)

