6.2: The Nature of Energy

Learning Objectives

• To understand the concept of energy and its various forms.
• To know the relationship between energy, work, and heat.

Because energy takes many forms, only some of which can be seen or felt, it is defined by its effect on matter. For example, microwave ovens produce energy to cook food, but we cannot see that energy. In contrast, we can see the energy produced by a light bulb when we switch on a lamp. In this section, we describe the forms of energy and discuss the relationship between energy, heat, and work.

Forms of Energy

The forms of energy include thermal energy, radiant energy, electrical energy, nuclear energy, and chemical energy (Figure \(\PageIndex{1}\)). Thermal energy results from atomic and molecular motion; the faster the motion, the greater the thermal energy. The temperature of an object is a measure of its thermal energy content. Radiant energy is the energy carried by light, microwaves, and radio waves. Objects left in bright sunshine or exposed to microwaves become warm because much of the radiant energy they absorb is converted to thermal energy. Electrical energy results from the flow of electrically charged particles. When the ground and a cloud develop a separation of charge, for example, the resulting flow of electrons from one to the other produces lightning, a natural form of electrical energy. Nuclear energy is stored in the nucleus of an atom, and chemical energy is stored within a chemical compound because of a particular arrangement of atoms.

Figure \(\PageIndex{1}\): Forms of Energy. (a) Thermal energy results from atomic and molecular motion; molten steel at 2000°C has a very high thermal energy content. (b) Radiant energy (e.g., from the sun) is the energy in light, microwaves, and radio waves. (c) Lightning is an example of electrical energy, which is due to the flow of electrically charged particles. (d) Nuclear energy is released when particles in the nucleus of the atom are rearranged. (e) Chemical energy results from the particular arrangement of atoms in a chemical compound; the heat and light produced in this reaction are due to energy released during the breaking and reforming of chemical bonds.

Electrical energy, nuclear energy, and chemical energy are different forms of potential energy (PE), which is energy stored in an object because of the relative positions or orientations of its components. A brick lying on the windowsill of a 10th-floor office has a great deal of potential energy, but until its position changes by falling, the energy is contained. In contrast, kinetic energy (KE) is energy due to the motion of an object. When the brick falls, its potential energy is transformed to kinetic energy, which is then transferred to the object on the ground that it strikes. The electrostatic attraction between oppositely charged particles is a form of potential energy, which is converted to kinetic energy when the charged particles move toward each other.

Energy can be converted from one form to another (Figure \(\PageIndex{2}\)) or, as we saw with the brick, transferred from one object to another. For example, when you climb a ladder to a high diving board, your body uses chemical energy produced by the combustion of organic molecules. As you climb, the chemical energy is converted to mechanical work to overcome the force of gravity. When you stand on the end of the diving board, your potential energy is greater than it was before you climbed the ladder: the greater the distance from the water, the greater the potential energy. When you then dive into the water, your potential energy is converted to kinetic energy as you fall, and when you hit the surface, some of that energy is transferred to the water, causing it to splash into the air. Chemical energy can also be converted to radiant energy; one common example is the light emitted by fireflies, which is produced from a chemical reaction.

Figure \(\PageIndex{2}\): Interconversion of Forms of Energy. When a swimmer steps off the platform to dive into the water, potential energy is converted to kinetic energy. As the swimmer climbs back up to the top of the diving platform, chemical energy is converted to mechanical work.

Although energy can be converted from one form to another, the total amount of energy in the universe remains constant. This is known as the law of conservation of energy: Energy cannot be created or destroyed.

Energy, Heat, and Work

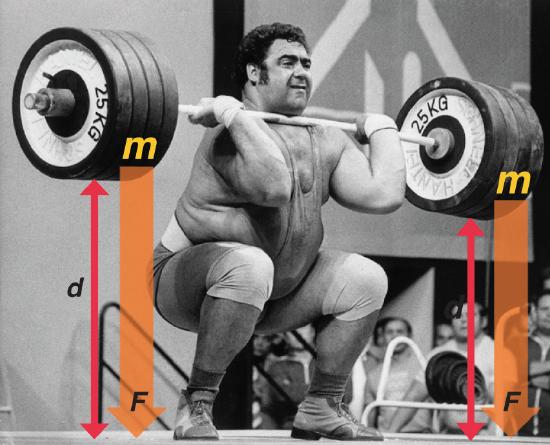
One definition of energy is the capacity to do work. The easiest form of work to visualize is mechanical work (Figure \(\PageIndex{3}\)), which is the energy required to move an object a distance d when opposed by a force F, such as gravity:

work = force x distance

\[w=F\,d \label{5.1.1} \]

Because the force (F) that opposes the action is equal to the mass (m) of the object times its acceleration (a), we can also write Equation \(\ref{5.1.1}\) as follows:

work= mass x acceleration x distance

\[w = m\,a\,d \label{5.1.2} \]

Recall from that weight is a force caused by the gravitational attraction between two masses, such as you and Earth.

Consider the mechanical work required for you to travel from the first floor of a building to the second. Whether you take an elevator or an escalator, trudge upstairs, or leap up the stairs two at a time, energy is expended to overcome the force of gravity. The amount of work done (w) and thus the energy required depends on three things:

1. the height of the second floor (the distance d);
2. your mass, which must be raised that distance against the downward acceleration due to gravity; and
3. your path.

Figure \(\PageIndex{2}\): An Example of Mechanical Work. One form of energy is mechanical work, the energy required to move an object of mass m a distance d when opposed by a force F, such as gravity.

In contrast, heat (q) is thermal energy that can be transferred from an object at one temperature to an object at another temperature. The net transfer of thermal energy stops when the two objects reach the same temperature.

Energy is an extensive property of matter—for example, the amount of thermal energy in an object is proportional to both its mass and its temperature. A water heater that holds 150 L of water at 50°C contains much more thermal energy than does a 1 L pan of water at 50°C. Similarly, a bomb contains much more chemical energy than does a firecracker. We now present a more detailed description of kinetic and potential energy.

Kinetic and Potential Energy

The kinetic energy of an object is related to its mass \(m\) and velocity \(v\):

\[KE=\dfrac{1}{2}mv^2 \label{5.1.4} \]

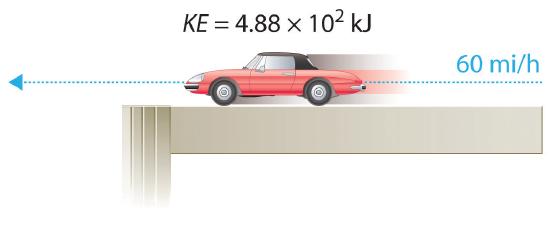
For example, the kinetic energy of a 1360 kg (approximately 3000 lb) automobile traveling at a velocity of 26.8 m/s (approximately 60 mi/h) is

\[KE=\dfrac{1}{2}(1360 kg)(26.8 ms)^2= 4.88 \times 10^5 g \cdot m^2 \label{5.1.5} \]

Because all forms of energy can be interconverted, energy in any form can be expressed using the same units as kinetic energy. The SI unit of energy, the joule (J), is named after the British physicist James Joule (1818–1889), an early worker in the field of energy. is defined as 1 kilogram·meter²/second² (kg·m²/s²). Because a joule is such a small quantity of energy, chemists usually express energy in kilojoules (1 kJ = 10³ J). For example, the kinetic energy of the 1360 kg car traveling at 26.8 m/s is 4.88 × 10⁵ J or 4.88 × 10² kJ. It is important to remember that the units of energy are the same regardless of the form of energy, whether thermal, radiant, chemical, or any other form. Because heat and work result in changes in energy, their units must also be the same.

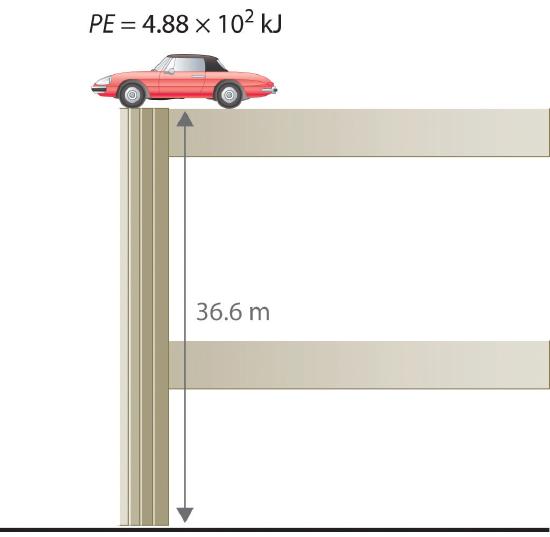
To demonstrate, let’s calculate the potential energy of the same 1360 kg automobile if it were parked on the top level of a parking garage 36.6 m (120 ft) high. Its potential energy is equivalent to the amount of work required to raise the vehicle from street level to the top level of the parking garage, which is w = Fd. According to Equation \(\ref{5.1.2}\), the force (F) exerted by gravity on any object is equal to its mass (m, in this case, 1360 kg) times the acceleration (a) due to gravity (g, 9.81 m/s² at Earth’s surface). The distance (d) is the height (h) above street level (in this case, 36.6 m). Thus the potential energy of the car is as follows:

\[ PE= F\;d = m\,a\;d = m\,g\,h \label{5.1.6a} \]

\[PE=(1360, Kg)\left(\dfrac{9.81\, m}{s^2}\right)(36.6\;m) = 4.88 \times 10^5\; \frac{Kg \cdot m}{s^2} \label{5.1.6b} \]

\[=4.88 \times 10^5 J = 488\; kJ \label{5.1.6c} \]

The units of potential energy are the same as the units of kinetic energy. Notice that in this case the potential energy of the stationary automobile at the top of a 36.6 m high parking garage is the same as its kinetic energy at 60 mi/h.

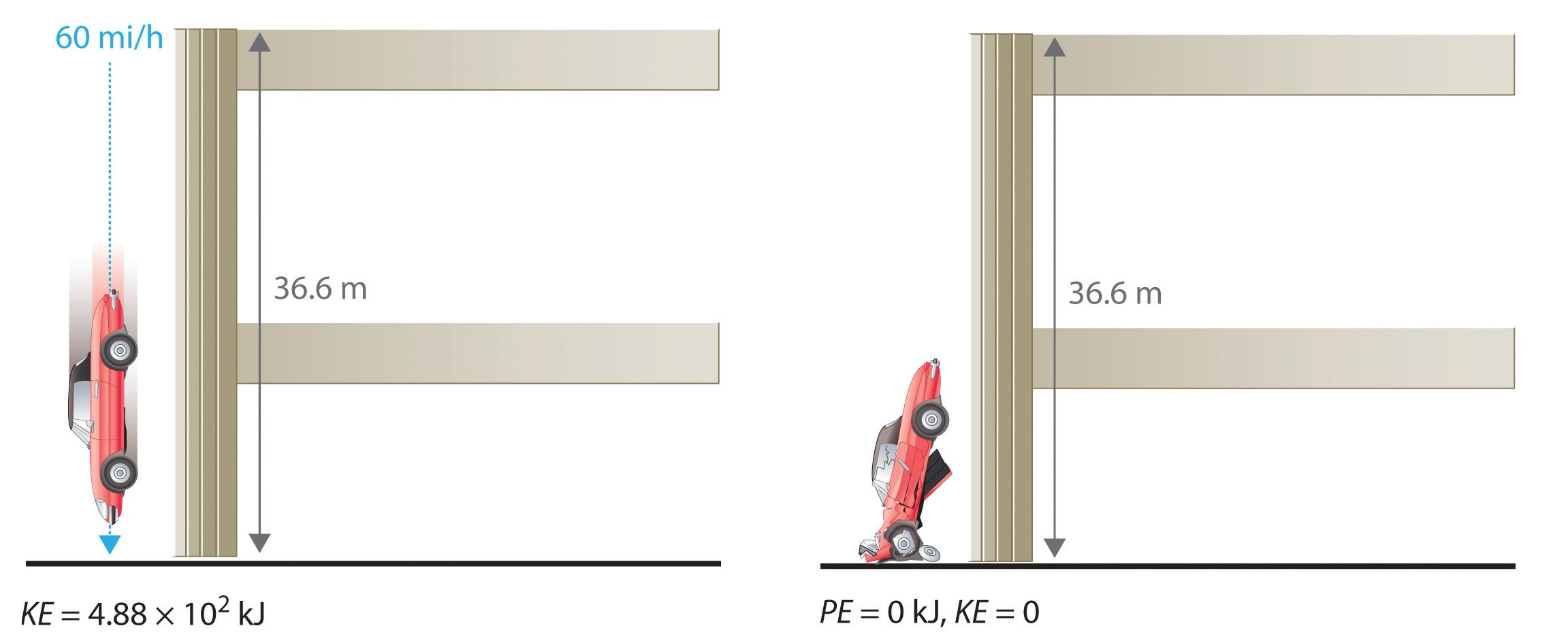
If the vehicle fell from the roof of the parking garage, its potential energy would be converted to kinetic energy, and it is reasonable to infer that the vehicle would be traveling at 60 mi/h just before it hit the ground, neglecting air resistance. After the car hit the ground, its potential and kinetic energy would both be zero.

Potential energy is usually defined relative to an arbitrary standard position (in this case, the street was assigned an elevation of zero). As a result, we usually calculate only differences in potential energy: in this case, the difference between the potential energy of the car on the top level of the parking garage and the potential energy of the same car on the street at the base of the garage.

When the car is falling from the top of the parking structure it has a kinetic energy of 488 kilojoules. When the car hits the floor is has a potential and kinetic energy of zero.

Units of Energy

The units of energy are the same for all forms of energy. Energy can also be expressed in the non-SI units of calories (cal), where 1 cal was originally defined as the amount of energy needed to raise the temperature of exactly 1 g of water from 14.5°C to 15.5°C.We specify the exact temperatures because the amount of energy needed to raise the temperature of 1 g of water 1°C varies slightly with elevation. To three significant figures, however, this amount is 1.00 cal over the temperature range 0°C–100°C. The name is derived from the Latin calor, meaning “heat.” Although energy may be expressed as either calories or joules, calories were defined in terms of heat, whereas joules were defined in terms of motion. Because calories and joules are both units of energy, however, the calorie is now defined in terms of the joule:

\[1 \;cal = 4.184 \;J \;\text{exactly} \label{5.1.7a} \]

\[1 \;J = 0.2390\; cal \label{5.1.7b} \]

In this text, we will use the SI units—joules (J) and kilojoules (kJ)—exclusively, except when we deal with nutritional information.

Example \(\PageIndex{1}\)

1. If the mass of a baseball is 149 g, what is the kinetic energy of a fastball clocked at 100 mi/h?
2. A batter hits a pop fly, and the baseball (with a mass of 149 g) reaches an altitude of 250 ft. If we assume that the ball was 3 ft above home plate when hit by the batter, what is the increase in its potential energy?

Given: mass and velocity or height

Asked for: kinetic and potential energy

Strategy:

Use Equation 5.1.4 to calculate the kinetic energy and Equation 5.1.6 to calculate the potential energy, as appropriate.

Solution:

1. The kinetic energy of an object is given by \( \frac{1}{2} mv^2\) In this case, we know both the mass and the velocity, but we must convert the velocity to SI units: \[ v= \left(\dfrac{100\; \cancel{mi}}{1\;\cancel{h}} \right) \left(\dfrac{1 \;\cancel{h}}{60 \;\cancel{min}} \right) \left(\dfrac{1 \; \cancel{min}}{60 \;s} \right)\left(\dfrac{1.61\; \cancel{km}}{1 \;\cancel{mi}} \right) (\dfrac{1000\; m}{1\; \cancel{km}})= 44.7 \;m/s \nonumber \]

   The kinetic energy of the baseball is therefore \[
   KE= 1492 \;\cancel{g} \left(\dfrac{1\; kg}{1000 \;\cancel{g}} \right) \left(\dfrac{44.7 \;m}{s} \right)^2= 1.49 \times 10^2 \dfrac{kg⋅m^2}{s^2}= 1.49 \times10^2\; J \nonumber \]

2. The increase in potential energy is the same as the amount of work required to raise the ball to its new altitude, which is (250 − 3) = 247 feet above its initial position. Thus \[ PE= 149\;\cancel{g} \left(\dfrac{1\; kg}{1000\; \cancel{g}} \right)\left(\dfrac{9.81\; m}{s^2} \right) \left(247\; \cancel{ft} \right) \left(\dfrac{0.3048\; m}{1 \;\cancel{ft}} \right)= 1.10 \times 10^2 \dfrac{kg⋅m^2}{s^2}= 1.10 \times 10^2\; J \nonumber \]

Exercise \(\PageIndex{1}\)

1. In a bowling alley, the distance from the foul line to the head pin is 59 ft, 10 13/16 in. (18.26 m). If a 16 lb (7.3 kg) bowling ball takes 2.0 s to reach the head pin, what is its kinetic energy at impact? (Assume its speed is constant.)
2. What is the potential energy of a 16 lb bowling ball held 3.0 ft above your foot?

Answer a

3.10 × 10² J

Answer b

65 J

Summary

All forms of energy can be interconverted. Three things can change the energy of an object: the transfer of heat, work performed on or by an object, or some combination of heat and work. Thermochemistry is a branch of chemistry that qualitatively and quantitatively describes the energy changes that occur during chemical reactions. Energy is the capacity to do work. Mechanical work is the amount of energy required to move an object a given distance when opposed by a force. Thermal energy is due to the random motions of atoms, molecules, or ions in a substance. The temperature of an object is a measure of the amount of thermal energy it contains. Heat (q) is the transfer of thermal energy from a hotter object to a cooler one. Energy can take many forms; most are different varieties of potential energy (PE), energy caused by the relative position or orientation of an object. Kinetic energy (KE) is the energy an object possesses due to its motion. The most common units of energy are the joule (J), defined as 1 (kg·m²)/s², and the calorie, defined as the amount of energy needed to raise the temperature of 1 g of water by 1°C (1 cal = 4.184 J).