3.7 Balancing Chemical Equations
- Page ID
- 33870
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To balance equations that describe reactions in solution.
- To calculate the quantities of compounds produced or consumed in a chemical reaction.
- To solve quantitative problems involving the stoichiometry of reactions in solution.
A balanced chemical equation gives the identity of the reactants and the products as well as the accurate number of molecules or moles of each that are consumed or produced. Stoichiometry is a collective term for the quantitative relationships between the masses, the numbers of moles, and the numbers of particles (atoms, molecules, and ions) of the reactants and the products in a balanced chemical equation. A stoichiometric quantity is the amount of product or reactant specified by the coefficients in a balanced chemical equation. This section describes how to use the stoichiometry of a reaction to answer questions like the following: How much oxygen is needed to ensure complete combustion of a given amount of isooctane? (This information is crucial to the design of nonpolluting and efficient automobile engines.) How many grams of pure gold can be obtained from a ton of low-grade gold ore? (The answer determines whether the ore deposit is worth mining.) If an industrial plant must produce a certain number of tons of sulfuric acid per week, how much elemental sulfur must arrive by rail each week?
All these questions can be answered using the concepts of the mole, molar and formula masses, and solution concentrations, along with the coefficients in the appropriate balanced chemical equation.
Stoichiometry Problems
When carrying out a reaction in either an industrial setting or a laboratory, it is easier to work with masses of substances than with the numbers of molecules or moles. The general method for converting from the mass of any reactant or product to the mass of any other reactant or product using a balanced chemical equation is outlined in and described in the following text.
Steps in Converting between Masses of Reactant and Product
- Convert the mass of one substance (substance A) to the corresponding number of moles using its molar mass.
- From the balanced chemical equation, obtain the number of moles of another substance (B) from the number of moles of substance A using the appropriate mole ratio (the ratio of their coefficients).
- Convert the number of moles of substance B to mass using its molar mass. It is important to remember that some species are present in excess by virtue of the reaction conditions. For example, if a substance reacts with the oxygen in air, then oxygen is in obvious (but unstated) excess.
Converting amounts of substances to moles—and vice versa—is the key to all stoichiometry problems, whether the amounts are given in units of mass (grams or kilograms), weight (pounds or tons), or volume (liters or gallons).
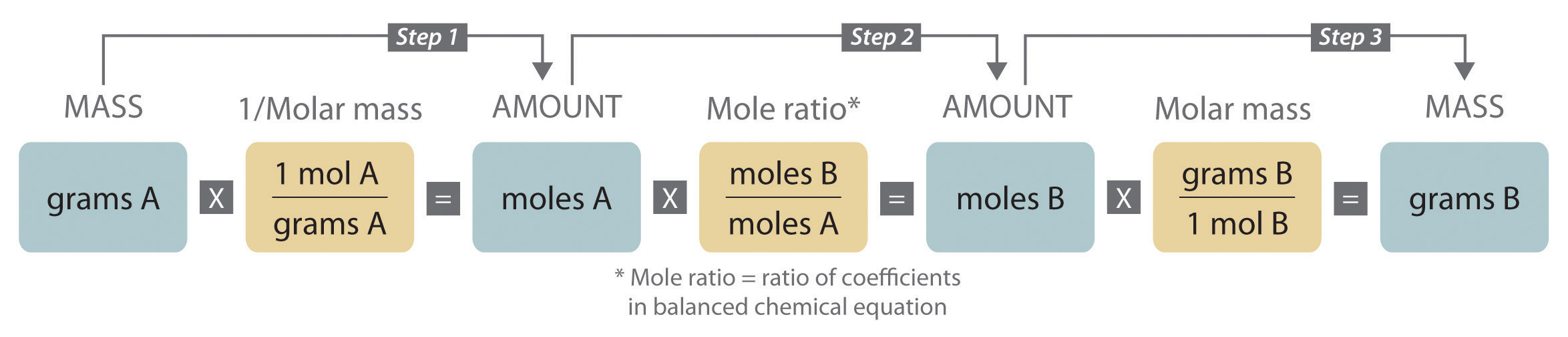
To illustrate this procedure, consider the combustion of glucose. Glucose reacts with oxygen to produce carbon dioxide and water:
\[ C_6H_{12}O_6 (s) + 6 O_2 (g) \rightarrow 6 CO_2 (g) + 6 H_2O (l) \label{3.6.1} \]
Just before a chemistry exam, suppose a friend reminds you that glucose is the major fuel used by the human brain. You therefore decide to eat a candy bar to make sure that your brain does not run out of energy during the exam (even though there is no direct evidence that consumption of candy bars improves performance on chemistry exams). If a typical 2 oz candy bar contains the equivalent of 45.3 g of glucose and the glucose is completely converted to carbon dioxide during the exam, how many grams of carbon dioxide will you produce and exhale into the exam room?
The initial step in solving a problem of this type is to write the balanced chemical equation for the reaction. Inspection shows that it is balanced as written, so the strategy outlined above can be adapted as follows:
1. Use the molar mass of glucose (to one decimal place, 180.2 g/mol) to determine the number of moles of glucose in the candy bar:
\[ moles \, glucose = 45.3 \, g \, glucose \times {1 \, mol \, glucose \over 180.2 \, g \, glucose } = 0.251 \, mol \, glucose \nonumber \]
2. According to the balanced chemical equation, 6 mol of CO2 is produced per mole of glucose; the mole ratio of CO2 to glucose is therefore 6:1. The number of moles of CO2 produced is thus
\[ moles \, CO_2 = mol \, glucose \times {6 \, mol \, CO_2 \over 1 \, mol \, glucose } \nonumber \]
\[ = 0.251 \, mol \, glucose \times {6 \, mol \, CO_2 \over 1 \, mol \, glucose } \nonumber \]
\[ = 1.51 \, mol \, CO_2 \nonumber \]
3. Use the molar mass of CO2 (44.010 g/mol) to calculate the mass of CO2 corresponding to 1.51 mol of CO2:
\[ mass\, of\, CO_2 = 1.51 \, mol \, CO_2 \times {44.010 \, g \, CO_2 \over 1 \, mol \, CO_2} = 66.5 \, g \, CO_2 \nonumber \]
These operations can be summarized as follows:
\[ 45.3 \, g \, glucose \times {1 \, mol \, glucose \over 180.2 \, g \, glucose} \times {6 \, mol \, CO_2 \over 1 \, mol \, glucose} \times {44.010 \, g \, CO_2 \over 1 \, mol \, CO_2} = 66.4 \, g \, CO_2 \nonumber \]
Discrepancies between the two values are attributed to rounding errors resulting from using stepwise calculations in steps 1–3. (Remember that you should generally carry extra significant digits through a multistep calculation to the end to avoid this!) This amount of gaseous carbon dioxide occupies an enormous volume—more than 33 L. Similar methods can be used to calculate the amount of oxygen consumed or the amount of water produced.
The balanced chemical equation was used to calculate the mass of product that is formed from a certain amount of reactant. It can also be used to determine the masses of reactants that are necessary to form a certain amount of product or, as shown in Example \(\PageIndex{1}\), the mass of one reactant that is required to consume a given mass of another reactant.
The combustion of hydrogen with oxygen to produce gaseous water is extremely vigorous, producing one of the hottest flames known. Because so much energy is released for a given mass of hydrogen or oxygen, this reaction was used to fuel the NASA (National Aeronautics and Space Administration) space shuttles, which have recently been retired from service. NASA engineers calculated the exact amount of each reactant needed for the flight to make sure that the shuttles did not carry excess fuel into orbit. Calculate how many tons of hydrogen a space shuttle needed to carry for each 1.00 tn of oxygen (1 tn = 2000 lb).
The US space shuttle Discovery during liftoff. The large cylinder in the middle contains the oxygen and hydrogen that fueled the shuttle’s main engine.
Given: reactants, products, and mass of one reactant
Asked for: mass of other reactant
Strategy:
- Write the balanced chemical equation for the reaction.
- Convert mass of oxygen to moles. From the mole ratio in the balanced chemical equation, determine the number of moles of hydrogen required. Then convert the moles of hydrogen to the equivalent mass in tons.
Solution:
We use the same general strategy for solving stoichiometric calculations as in the preceding example. Because the amount of oxygen is given in tons rather than grams, however, we also need to convert tons to units of mass in grams. Another conversion is needed at the end to report the final answer in tons.
A We first use the information given to write a balanced chemical equation. Because we know the identity of both the reactants and the product, we can write the reaction as follows:
\[ H_2 (g) + O_2 (g) \rightarrow H_2O (g) \nonumber \]
This equation is not balanced because there are two oxygen atoms on the left side and only one on the right. Assigning a coefficient of 2 to both H2O and H2 gives the balanced chemical equation:
\[ 2 H_2 (g) + O_2 (g) \rightarrow 2 H_2O (g) \nonumber \]
Thus 2 mol of H2 react with 1 mol of O2 to produce 2 mol of H2O.
1. B To convert tons of oxygen to units of mass in grams, we multiply by the appropriate conversion factors:
\[ mass \, of \, O_2 = 1.00 \, tn \times { 2000 \, lb \over tn} \times {453.6 \, g \over lb} = 9.07 \times 10^5 \, g \, O_2 \nonumber \]
Using the molar mass of O2 (32.00 g/mol, to four significant figures), we can calculate the number of moles of O2 contained in this mass of O2:
\[ mol \, O_2 = 9.07 \times 10^5 \, g \, O_2 \times {1 \, mol \, O_2 \over 32.00 \, g \, O_2} = 2.83 \times 10^4 \, mol \, O_2 \nonumber \]
2. Now use the coefficients in the balanced chemical equation to obtain the number of moles of H2 needed to react with this number of moles of O2:
\[ mol \, H_2 = mol \, O_2 \times {2 \, mol \, H_2 \over 1 \, mol \, O_2} \nonumber \]
\[ = 2.83 \times 10^4 \, mol \, O_2 \times {2 \, mol \, H_2 \over 1 \, mol \, O_2} = 5.66 \times 10^4 \, mol \, H_2 \nonumber \]
3. The molar mass of H2 (2.016 g/mol) allows us to calculate the corresponding mass of H2:
\[mass \, of \, H_2 = 5.66 \times 10^4 \, mol \, H_2 \times {2.016 \, g \, H_2 \over mol \, H_2} = 1.14 \times 10^5 \, g \, H_2 \nonumber \]
Finally, convert the mass of H2 to the desired units (tons) by using the appropriate conversion factors:
\[ tons \, H_2 = 1.14 \times 10^5 \, g \, H_2 \times {1 \, lb \over 453.6 \, g} \times {1 \, tn \over 2000 \, lb} = 0.126 \, tn \, H_2 \nonumber \]
The space shuttle had to be designed to carry 0.126 tn of H2 for each 1.00 tn of O2. Even though 2 mol of H2 are needed to react with each mole of O2, the molar mass of H2 is so much smaller than that of O2 that only a relatively small mass of H2 is needed compared to the mass of O2.
Cinnabar, (or Cinnabarite) \(HgS\) is the common ore of mercury. Because of its mercury content, cinnabar can be toxic to human beings; however, because of its red color, it has also been used since ancient times as a pigment.

Alchemists produced elemental mercury by roasting cinnabar ore in air:
\[ HgS (s) + O_2 (g) \rightarrow Hg (l) + SO_2 (g) \nonumber \]
The volatility and toxicity of mercury make this a hazardous procedure, which likely shortened the life span of many alchemists. Given 100 g of cinnabar, how much elemental mercury can be produced from this reaction?
- Answer
-
86.2 g
Calculating Moles from Volume
Quantitative calculations involving reactions in solution are carried out with masses, however, volumes of solutions of known concentration are used to determine the number of moles of reactants. Whether dealing with volumes of solutions of reactants or masses of reactants, the coefficients in the balanced chemical equation give the number of moles of each reactant needed and the number of moles of each product that can be produced. An expanded version of the flowchart for stoichiometric calculations is shown in Figure \(\PageIndex{2}\). The balanced chemical equation for the reaction and either the masses of solid reactants and products or the volumes of solutions of reactants and products can be used to determine the amounts of other species, as illustrated in the following examples.

The balanced chemical equation for a reaction and either the masses of solid reactants and products or the volumes of solutions of reactants and products can be used in stoichiometric calculations.
Gold is extracted from its ores by treatment with an aqueous cyanide solution, which causes a reaction that forms the soluble [Au(CN)2]− ion. Gold is then recovered by reduction with metallic zinc according to the following equation:
\[ Zn(s) + 2[Au(CN)_2]^-(aq) \rightarrow [Zn(CN)_4]^{2-}(aq) + 2Au(s) \nonumber \]
What mass of gold can be recovered from 400.0 L of a 3.30 × 10−4 M solution of [Au(CN)2]−?
Given: chemical equation and molarity and volume of reactant
Asked for: mass of product
Strategy:
- Check the chemical equation to make sure it is balanced as written; balance if necessary. Then calculate the number of moles of [Au(CN)2]− present by multiplying the volume of the solution by its concentration.
- From the balanced chemical equation, use a mole ratio to calculate the number of moles of gold that can be obtained from the reaction. To calculate the mass of gold recovered, multiply the number of moles of gold by its molar mass.
Solution:
A The equation is balanced as written; proceed to the stoichiometric calculation. Figure \(\PageIndex{2}\) is adapted for this particular problem as follows:

As indicated in the strategy, start by calculating the number of moles of [Au(CN)2]− present in the solution from the volume and concentration of the [Au(CN)2]− solution:
\( \begin{align} moles\: [Au(CN)_2 ]^-
& = V_L M_{mol/L} \\
& = 400 .0\: \cancel{L} \left( \dfrac{3 .30 \times 10^{4-}\: mol\: [Au(CN)_2 ]^-} {1\: \cancel{L}} \right) = 0 .132\: mol\: [Au(CN)_2 ]^- \end{align} \)
B Because the coefficients of gold and the [Au(CN)2]− ion are the same in the balanced chemical equation, assuming that Zn(s) is present in excess, the number of moles of gold produced is the same as the number of moles of [Au(CN)2]− (i.e., 0.132 mol of Au). The problem asks for the mass of gold that can be obtained, so the number of moles of gold must be converted to the corresponding mass using the molar mass of gold:
\( \begin{align} mass\: of\: Au &= (moles\: Au)(molar\: mass\: Au) \\
&= 0 .132\: \cancel{mol\: Au} \left( \dfrac{196 .97\: g\: Au} {1\: \cancel{mol\: Au}} \right) = 26 .0\: g\: Au \end{align}\)
At a 2011 market price of over $1400 per troy ounce (31.10 g), this amount of gold is worth $1170.
\( 26 .0\: \cancel{g\: Au} \times \dfrac{1\: \cancel{troy\: oz}} {31 .10\: \cancel{g}} \times \dfrac{\$1400} {1\: \cancel{troy\: oz\: Au}} = \$1170 \)
What mass of solid lanthanum(III) oxalate nonahydrate [La2(C2O4)3•9H2O] can be obtained from 650 mL of a 0.0170 M aqueous solution of LaCl3 by adding a stoichiometric amount of sodium oxalate?
- Answer
-
3.89 g
Finding Mols and Masses of Reactants and Products Using Stoichiometric Factors (Mol Ratios): Finding Mols and Masses of Reactants and Products Using Stoichiometric Factors, YouTube(opens in new window) [youtu.be]
Summary
Either the masses or the volumes of solutions of reactants and products can be used to determine the amounts of other species in the balanced chemical equation. Quantitative calculations that involve the stoichiometry of reactions in solution use volumes of solutions of known concentration instead of masses of reactants or products. The coefficients in the balanced chemical equation tell how many moles of reactants are needed and how many moles of product can be produced.


