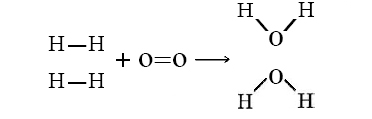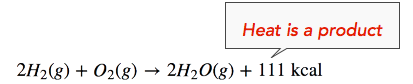A general statement, based on countless observations over centuries of study, is that all objects tend to move spontaneously to a position of minimum energy unless acted on by some other force or object.
Bond Dissociation Energy
Atoms bond together to form compounds because in doing so they attain lower energies than they possess as individual atoms. A quantity of energy, equal to the difference between the energies of the bonded atoms and the energies of the separated atoms, is released, usually as heat. That is, the bonded atoms have a lower energy than the individual atoms do. When atoms combine to make a compound, energy is always given off, and the compound has a lower overall energy. In making compounds, atoms act like a basketball on a playground slide; they move in the direction of decreasing energy.
We can reverse the process by putting energy into a molecule, which causes its bonds to break, separating the molecule into individual atoms. Bonds between certain specific elements usually have a characteristic energy, called the bond dissociation energy, that is needed to break the bond. The same amount of energy was liberated when the atoms made the chemical bond in the first place. The term bond dissociation energy is usually used to describe the strength of interactions between atoms that make covalent bonds. A C–C bond has an approximate bond energy of 80 kcal/mol, while a C=C has a bond energy of about 145 kcal/mol. The C=C bond is stronger than C-C (as discussed in relation to bond length in Section 4.4). For atoms in ionic compounds attracted by opposite charges, the term lattice energy is used. For now, we will deal with covalent bonds in molecules.
Although each molecule has its own characteristic bond dissociation energy, some generalizations are possible. For example, although the exact value of a C–H bond energy depends on the particular molecule, all C–H bonds have a bond energy of roughly the same value because they are all C–H bonds. It takes roughly 100 kcal of energy to break 1 mol of C–H bonds, so we speak of the bond dissociation energy of a C–H bond as being about 100 kcal/mol. Table \(\PageIndex{1}\) lists the approximate bond dissociation energies of various covalent bonds.
Table \(\PageIndex{1}\): Approximate Bond Dissociation Energies
| Bond |
Bond Dissociation Energy (kcal/mol) |
| C–H |
100 |
| C–O |
86 |
| C=O |
190 |
| C–N |
70 |
| C–C |
85 |
| C=C |
145 |
| C≡C |
200 |
| N–H |
93 |
| H–H |
105 |
| Br-Br |
46 |
| Cl–Cl |
58 |
| O–H |
110 |
| O=O |
119 |
| H–Br |
87 |
| H–Cl |
103 |
When a chemical reaction occurs, the atoms in the reactants rearrange their chemical bonds to make products. The new arrangement of bonds does not have the same total energy as the bonds in the reactants. Therefore, when chemical reactions occur, there will always be an accompanying energy change. The energy change, for a given reaction can be calculated using the bond dissociation energy values from Table \(\PageIndex{1}\).
Enthalpy Change or Heat of Reaction, ΔH
During a chemical reaction, bonds are broken and new bonds are formed. Breaking chemical bonds is endothermic, a process that requires an input of energy or absorption of heat. The reverse process of bond breaking is bond formation, which is exothermic, meaning it releases energy or gives off heat. The bond dissociation energy values listed in the above table give the amount of energy required to break a specific bond. When that same bond is reformed, an identical amount of energy is released. The numerical value of energy is the same for breaking and forming a bond, but the sign, or direction of the process is different. The overall energy change of a specific bond breaking and reforming would be zero, in other words energy is neither created or destroyed, following the law of conservation of energy.
In a chemical reaction, the bonds breaking are often different than the bonds reforming, sometimes there is more heat absorbed (more bonds are broken) and sometimes more heat is released (more bonds are formed). The measured difference between the total heat absorbed and the total heat released during a chemical reaction (performed at constant pressure) is called the heat of reaction or enthalpy change, and is represented by the symbol ΔH (where the Δ stands for change and the H represents enthalpy).
\[\text{enthalpy change} ≈ \Sigma\ (\text{bond dissociation energies}_{reactants}) - \Sigma\ (\text{bond dissociation energies}_{products})\]
The ≈ sign is used because we are adding together average bond dissociation energies; hence this approach does not give exact values for the enthalpy change, ΔH.
Let’s consider the reaction of 2 mols of hydrogen gas (H2) with 1 mol of oxygen gas (O2) to give 2 mol water:
\[2H_2(g)+O_2(g) \rightarrow 2H_2O(g)\]
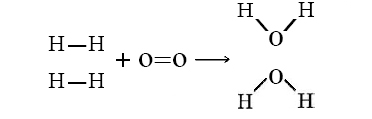
H–H = 105 kcal/mol O=O = 119 kcal/mol O–H = 110 kcal/mol
In this reaction, 2 H–H bonds and 1 O=O bonds from the reactant side are broken, while 4 O–H bonds (two for each H2O) are formed on the product side. The energy changes can be tabulated and calculated as follows:
| Reactant Bond Dissociation Energy (kcal/mol) |
Product Bond Dissociation Energy (kcal/mol) |
| 2 H–H |
2 mol x 105 kcal/mol = 210 kcal |
4 O–H |
4 mols x 110 kcal/mol = 440 kcal |
| 1 O=O |
1 mol x 119 kcal/mol = 119 kcal |
|
|
| |
Total = 329 kcal |
|
Total = 440 kcal |
\[\: \: \: \: \: \Delta H ≈ \Sigma\ (\text{bond dissociation energies}_{reactants}) - \Sigma\ (\text{bond dissociation energies}_{products})\]
\[\: \: \: \: \: \Delta H ≈ 329 \: \text{kcal} - 440 \: \text{kcal}\]
\[\: \: \: \: \: \Delta H ≈ −111 \: \text{kcal}\]
The enthalpy change (ΔH) of the reaction is approximately −111 kcal/mol. This means that bonds in the products (440 kcal) are stronger than the bonds in the reactants (329 kcal) by about 111 kcal/mol. Because the bonds in the products are stronger than those in the reactants, the reaction releases more energy than it absorbs. This excess energy is released as heat, so the reaction is exothermic. Hence, we can re-write the reaction with the heat released (111 kcal) on the product side of the equation, as follows:
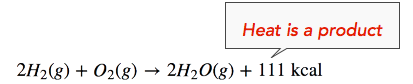
We can also re-write the reaction equation with the ΔH information (see below). Note that an exothermic reaction has a negative ΔH value.
\[2H_2(g)+O_2(g) \rightarrow 2H_2O(g)\ \: \: \: \: \: \Delta H = -111 \: \text{kcal}\]
Example \(\PageIndex{1}\)
What is the enthalpy change for this reaction? Is the reaction exothermic or endothermic?
\[H_2(g)+Br_2(g) \rightarrow 2HBr(g)\]
Solution
Step 1- First look at the equation and identify which bonds exist on in the reactants (bonds broken).
- one H-H bond and
- one Br-Br bond
Step 2- Do the same for the products (bonds formed)
Step 3- Identify the bond dissociation energies of these bonds from Table \(\PageIndex{1}\):
- H-H bonds: 105 kcal/mol
- Br-Br bonds: 46 kcal/mol
Step 4- Set up the table (see below) and apply the formula for enthalpy change.
| Reactant Bond Dissociation Energy (kcal/mol) |
Product Bond Dissociation Energy (kcal/mol) |
| 1 H–H |
1 mol x 105 kcal/mol = 105 kcal |
2 H–Br |
2 mols x 87 kcal/mol = 174 kcal |
| 1 Br–Br |
1 mol x 46 kcal/mol = 46 kcal |
|
|
| |
Total = 151 kcal |
|
Total = 174 kcal |
|
\[\: \: \: \: \: \Delta H ≈ 151 \: \text{kcal} - 174 \: \text{kcal}\]
\[\: \: \: \: \: \Delta H ≈ −23 \: \text{kcal}\]
|
Step 5- Since ΔH is negative (−23 kcal), the reaction is exothermic.
Exercise \(\PageIndex{1}\)
Using the bond dissociation energies given in the chart above, find the enthalpy change for the thermal decomposition of water:
\[H_2(g)+Cl_2(g) \rightarrow 2HCl(g)\]
Is the reaction written above exothermic or endothermic? Explain.
- Answer
-
ΔH = −43 kcal
Since ΔH is negative (−43 kcal), the reaction is exothermic.