1) You ask a classmate how much homework your chemistry professor assigned. Your classmate answers, “twenty.” Is that a proper answer? Why or why not?
2) Define significant figures. Why are they important?
3) Define the different types of zeros found in a number and explain whether or not they are significant.
4) Give the two conversion factors you can construct using each pair of units.
- meters and kilometers
- liters and microliters
- seconds and milliseconds
5) In general, how can you identify whether or not you have written the correct conversion factor for the problem?
6) Construct a conversion factor that can convert from one unit to the other in each pair of units.
- meter to km
- inch to cm
- pounds to kilogram
Scientific Notation
7) Convert each number into scientific notation.
- 100,000,000
- 0.0004970
- 30.01
- 2500
8) Convert each number into scientific notation.
- 304,300,000
- 0.0004
- 1000.
- 0.345
9) Convert each number into scientific notation.
- 736,350
- 0.0042
- 2500
- 0.478
10) Convert each number into decimal notation.
- 7.42 x 103
- 1.3 x 10-3
- 1.5 x 106
- 1.5147 x 10‑5
11) Convert each number into decimal notation.
- 8.62 x 104
- 5.5 x 10-3
- 1.02 x 10-6
- 6.03 x 10-10
12) Convert each number into decimal notation.
- 8.35 x 106
- 6.3 x 10-4
- 1.8 x 106
- 7.24 x 10-6
13) Fill in the blanks.
| |
Scientific Notation |
Decimal Notation |
| a) |
4.7 x103 |
|
| b) |
|
7,410. |
| c) |
9.3 x 10-4 |
|
| d) |
|
0.0045 |
14) Fill in the blanks.
| |
Scientific Notation |
Decimal Notation |
| a) |
5.36 x106 |
|
| b) |
|
1,120.0 |
| c) |
1.3 x 10-2 |
|
| d) |
|
0.010 |
15) Fill in the blanks.
| |
Scientific Notation |
Decimal Notation |
| a) |
8.4 x 105 |
|
| b) |
|
513 |
| c) |
6.30 x 10-6 |
|
| d) |
|
0.250 |
16. Use each diagram to report a measurement to the proper number of significant figures.
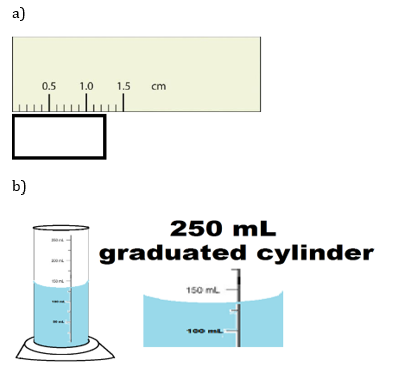
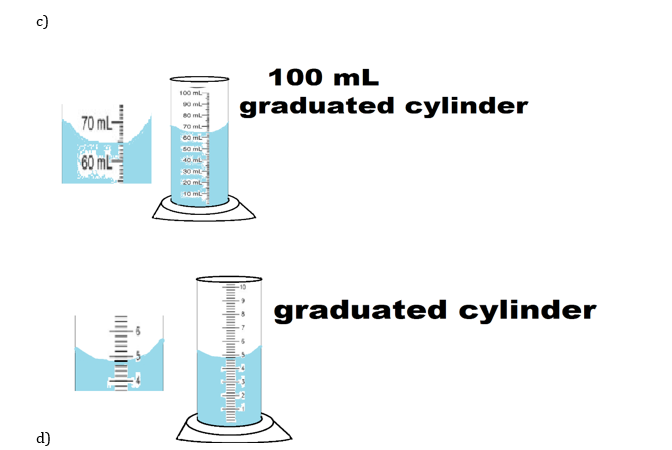
17) Use each diagram to report a measurement to the proper number of significant figures.
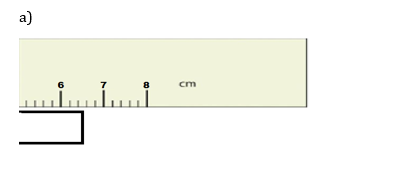
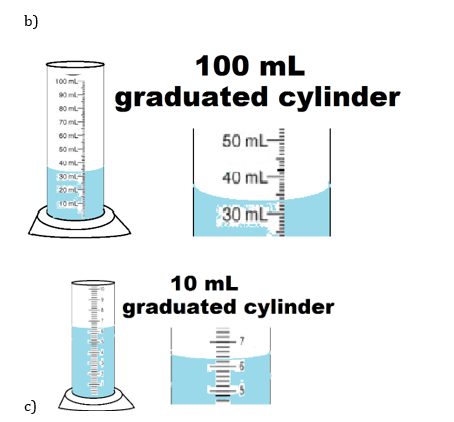
18) Use each diagram to report a measurement to the proper number of significant figures.
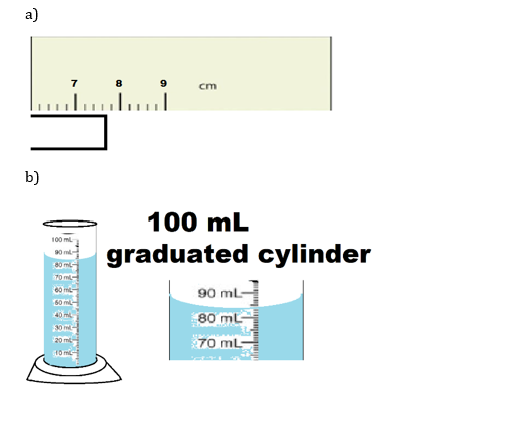
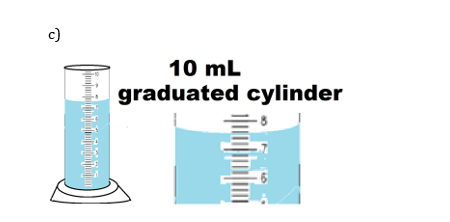
19) Give the number of significant figures in each. Identify the rule for each.
- 0.000140500 s
- 630,001 kg
- 155.000 in
- 0.0745 m
20) Give the number of significant figures in each. Identify the rule for each.
- 0.000250600 s
- 720,055 kg
- 589.560 in
- 0.0856 m
21) Give the number of significant figures in each. Identify the rule for each.
- 0.00540500 s
- 890,024 kg
- 729.770 in
- 0.0961 m
22) How many significant figures are in each number?
- 1.05
- 9,500
- 0.0004505
- 7563
23) How many significant figures are in each number?
- 0.00045050
- 7.210 × 106
- 5.005 × 10−6
- 4861
24) How many significant figures are in each number?
- 0.052010
- 0.3940
- 8200
- 8563
Rounding
25) Round each number to three significant figures.
- 24.632
- 0.34244
- 43,539
- 6.9978 x 106
26) Round each number to three significant figures.
- 35.743
- 0.45355
- 54640
- 7.0089 x 106
27) Round each number to three significant figures.
- 56.45
- 8.90443 × 108
- 1,000,000
- 0.9841
28) Determine if each number is rounded correctly to three significant figures. For any items that are incorrect, correct them.
- 3.459 x 103 to 3.5 x 103
- 4.874 x 103 to 50
- 87.42 to 87.4
- 0.09853 to 0.010
29) Determine if each number is rounded correctly to three significant figures. For any items that are incorrect, correct them.
- 4.560 x 103 to 4.5 x 103
- 8.514 x 103 to 85
- 93.72 to 93.7
- 0.05312 to 0.053
30) Determine if each number is rounded correctly to three significant figures. For any items that are incorrect, correct them.
- 5.670 x 103 to 5.7 x 103
- 5.783 x 103 to 60
- 87.42 to 87.4
- 0.023541 to 0.024
31) Complete the table.
| Number |
Rounded to 4 Significant Figures |
Rounded to 2 Significant Figures |
Rounded to 1 Significant Figure |
| a. 53.53229 |
53.53 |
54 |
5 x 101 |
| b.216.3535 |
|
|
|
| c. 0.36682 |
|
|
|
| d. 0.00888881 |
|
|
|
32) Complete the table.
| Number |
Rounded to 4 Significant Figures |
Rounded to 2 Significant Figures |
Rounded to 1 Significant Figure |
| a. 64.64320 |
64.64 |
64 |
6 x 101 |
| b.335.4545 |
|
|
|
| c. 0.54156 |
|
|
|
| d. 0.00777772 |
|
|
|
33) Complete the table.
| Number |
Rounded to 4 Significant Figures |
Rounded to 2 Significant Figures |
Rounded to 1 Significant Figure |
| a. 82.6268 |
82.63 |
83 |
8 x 101 |
| b.654.8545 |
|
|
|
| c. 0.75126 |
|
|
|
| d. 0.00777774 |
|
|
|
34) Determine if each calculation has the correct number of significant figures. For any items that are incorrect, correct them.
- 45.3254 x 59.00205 = 2674.3
- 0.00830 x 47.351 = 0.039
- 0.008070 / 5018.3 = 1.61811 x 10-6
- 0.04541 x 7143.5 = 324.39
35) Determine if each calculation has the correct number of significant figures. For any items that are incorrect, correct them.
- 105.34 x 47.334532 = 4986.22
- 0.047 x 23.3544 = 1.098
- 5.5225 / 503.455 = 0.010969
- 0.000154*1002.2 = 0.15
36) Determine if each calculation has the correct number of significant figures. For any items that are incorrect, correct them.
- 17.354 x 875.214 = 15100
- 0.0035 x 20.0456 = 0.07
- 0.00486 / 40.8954 = 0.000119
- 0.00225 * 2458.3 = 5.53
37) Determine if each calculation has the correct number of significant figures. For any items that are incorrect, correct them.
- 5.8 + 63.09 – 14 = 54.9
- 4301 – 2900.14 + 1.6 = 1402
- 0.00354 + 0.86 = 0.863
- 0.00974 – 0.008 = 0.00074
38) Determine if each calculation has the correct number of significant figures. For any items that are incorrect, correct them.
- 7.4 + 73.07 – 24 = 56.5
- 5323 – 3914.24 + 0.7 = 1409
- 0.00725 + 0.35 = 0.357
- 0.00653 – 0.003 = 0.00353
39) Determine if each calculation has the correct number of significant figures. For any items that are incorrect, correct them.
- 3.5 + 94.04 – 50 = 47.5
- 8206 – 5614.25 + 5.5 = 2597.25
- 0.00354 + 0.864 = 0.868
- 0.01874 – 0.010 = 0.00874
40) Determine if each calculation has the correct number of significant figures. For any items that are incorrect, correct them.
- (9.95 + 3.09) / 7.40000 = 1.762
- (1045.3 – 1.4) x 1.604 = 1674
- (749.40 + 6.7) / 4.54 = 1.6 x 102
- (845 / 301457) + 5.000198 = 5.00
41) Determine if each calculation has the correct number of significant figures. For any items that are incorrect, correct them.
- (8.65 + 2.85) / 8.96000 = 1.283
- (2252.5 – 2.8) x 2.765 = 6220
- (760.55 + 8.8) / 5.64 = 1.4 x 102
- (945 / 54147) + 4.51400014 = 4.53
42) Determine if each calculation has the correct number of significant figures. For any items that are incorrect, correct them.
- (1.24 + 3.14) / 4.54000 = 0.96
- (3251 – 3.6) x 6.54 = 21238
- (651.25 + 6.3) / 6.55 = 100
- (360 /64025) + 5.4100087 = 5.41
Unit Conversion
43) Convert the following metric quantities into the indicated units. Identify the number of significant figures in each answer.
- 1000. g into milligrams
- 6981 nm into meters
- 15 mL into liters
- 345 cm to millimeters
44) Convert the following metric quantities into the indicated units. Identify the number of significant figures in each answer.
- 8541 g into mg
- 7896 nm into m
- 25 kL into L
- 62 cm to mm
45) Convert the following metric quantities into the indicated units. Identify the number of significant figures in each answer.
- 34 kg to g
- 7539.34 nm to km
- 36 L into cL
- 109 cm to mm
46) Use English-to-Metric and Metric-to-English conversion factors to calculate the following:
- 87.6 ft into centimeters
- 557 yd to meters
- 645 feet to centimeters
- 7.0 inch to centimeters
47) Use English-to-Metric and Metric-to-English conversion factors to calculate the following:
- 90.7 ft into mm
- 14.8 lb to kg
- 400. m to mi
- 12.0 in to cm
48) Use English-to-Metric and Metric-to-English conversion factors to calculate the following:
- 71.3 ft to mm
- 15.2 lbs to kg
- 520. m to mi
- 8.0 in to cm
49) Fill in the blank to complete the table.
| m |
km |
mm |
nm |
pm |
| 6.02 x10-5 m |
|
6.02 x 10-2 mm |
|
|
| |
|
|
|
25.3 pm |
| |
|
|
225 nm |
|
| |
8.22 x 10-3 km |
|
|
|
| |
|
4.2 x 105 mm |
|
|
50) Fill in the blank to complete the table.
| m |
km |
mm |
nm |
pm |
| 5.36 x10-5 m |
|
5.36 x 10-2 mm |
|
|
| |
|
|
|
18.7 pm |
| |
|
|
345 nm |
|
| |
6.33 x 10-3 km |
|
|
|
| |
|
5.5 x 105 mm |
|
|
51) Fill in the blank to complete the table.
| m |
km |
mm |
nm |
pm |
| 1.88 x10-5 m |
|
1.88 x 10-2 mm |
|
|
| |
|
|
|
14.3 pm |
| |
|
|
365 nm |
|
| |
6.34 x 10-3 km |
|
|
|
| |
|
6.9 x 105 mm |
|
|
Unit Raised to a Power
52) Perform each conversion.
- 1.2 ft2 = _____in2
- 1.2 yd2 = _______ft2
- 1.2 m3 = _______ yd3
53) Perform each conversion.
- 2.4 ft2 = _____in2
- 2.4 yd2 = _______ft2
- 2.4 m3 = _______ yd3
54) Perform each conversion.
- 3.5 ft2 = _____in2
- 3.5 yd2 = _______ft2
- 35 m3 = _______ yd3
55) A pizza has an area of 3.44 m2. Convert the pizza’s area to each of the following units.
- in2
- mm2
- km2
56) A pizza has an area of 2.50 m2. Convert the pizza’s area to each of the following units.
- in2
- mm2
- km2
57) A pizza has an area of 13.5 m2. Convert the pizza’s area to each of the following units.
- in2
- mm2
- km2
Density
58) A copper strip has a mass of 4.67 g and a volume of 0.523 cm3. What is the density of the copper strip? Is the strip pure copper?
59) A lead strip has a mass of 7.41 g and a volume of 0.654 cm3. What is the density of the lead strip? Is the strip pure lead?
60) A silver ingot has a mass of 70.34 g and a volume of 8.5 cm3. What is the density of the ingot? Is the ingot pure silver?
61) Given that the density of gold is 19.3 g/cm3,
- Determine the mass of gold (in grams) in an ingot with a volume of 121 cm3.
- Determine the volume of gold (in cm3) in an ingot with a mass of 1354 g.
62) Given that the density of Cu is 8.93 g/cm3,
- Determine the mass of copper (in grams) in a copper strip with a volume of 433.0 cm3.
- Determine the volume of copper (in cm3) in a copper strip with a mass of 502.34 grams.
63) Given that the density of lead is 11.34 g/cm3,
- Determine the mass of lead (in grams) in a lead block with a volume of 607.9 cm3.
- Determine the volume of lead (in cm3) in a lead block with a mass of 802.35 grams.
Cumulative Problems
64) If the walls in a room are 955 square feet in area, and a gallon of paint covers 15 square yards, how many gallons of paint are needed to paint the walls in the room? (3 ft = 1 yd)
65) Gas is sold for $1.399 per liter in Toronto, Canada. Your car needs 12.00 gallons. How much will your credit card be charged in Canadian dollars (minus tax)?
66) If an object has a density of 8.65 g/cm3, what is its density in units of kg/m3?
67) Water is being pumped out of a reservoir at a rate of 2.54 liters per 15.0 seconds. If the reservoir contains 1.0500 x 106 gallons of water, how many hours will it take to empty it?
68) The mass of an average blueberry is 0.75 g and the mass of an automobile is 2,010.3 kg. Find the number of automobiles whose total mass is the same as 1.0 x 1010 blueberries?
69) Tom and Mary both have farms. Tom raises chickens for eggs while Mary plants apples. 3.00 lb of apples can be exchanged with 1 dozen eggs. If Tom has 130. eggs to exchange with Mary, how many pounds of apples will he get?
70) Calculate the number of seconds in 1.00 year.







