4.4: Molecules with multiple chiral centers

Last updated
Save as PDF

Page ID: 225781

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

So far, we have been analyzing compounds with a single chiral center. Next, we turn our attention to those which have multiple chiral centers. We’ll start with some stereoisomeric four-carbon sugars with two chiral centers.

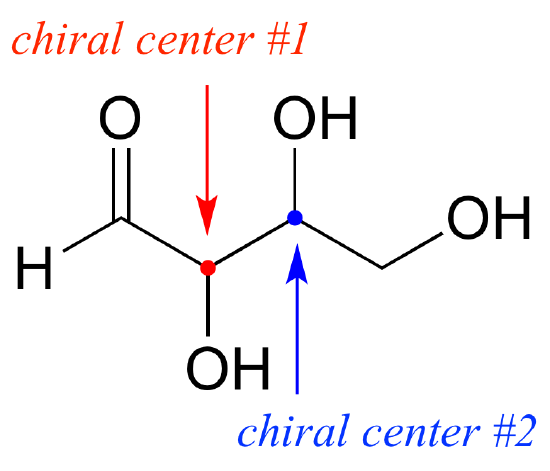
To avoid confusion, we will simply refer to the different stereoisomers by capital letters.

Look first at compound A below. Both chiral centers in have the R configuration (you should confirm this for yourself!). The mirror image of Compound A is compound B, which has the S configuration at both chiral centers. If we were to pick up compound A, flip it over and put it next to compound B, we would see that they are not superimposable (again, confirm this for yourself with your models!). A and B are nonsuperimposable mirror images: in other words, enantiomers.

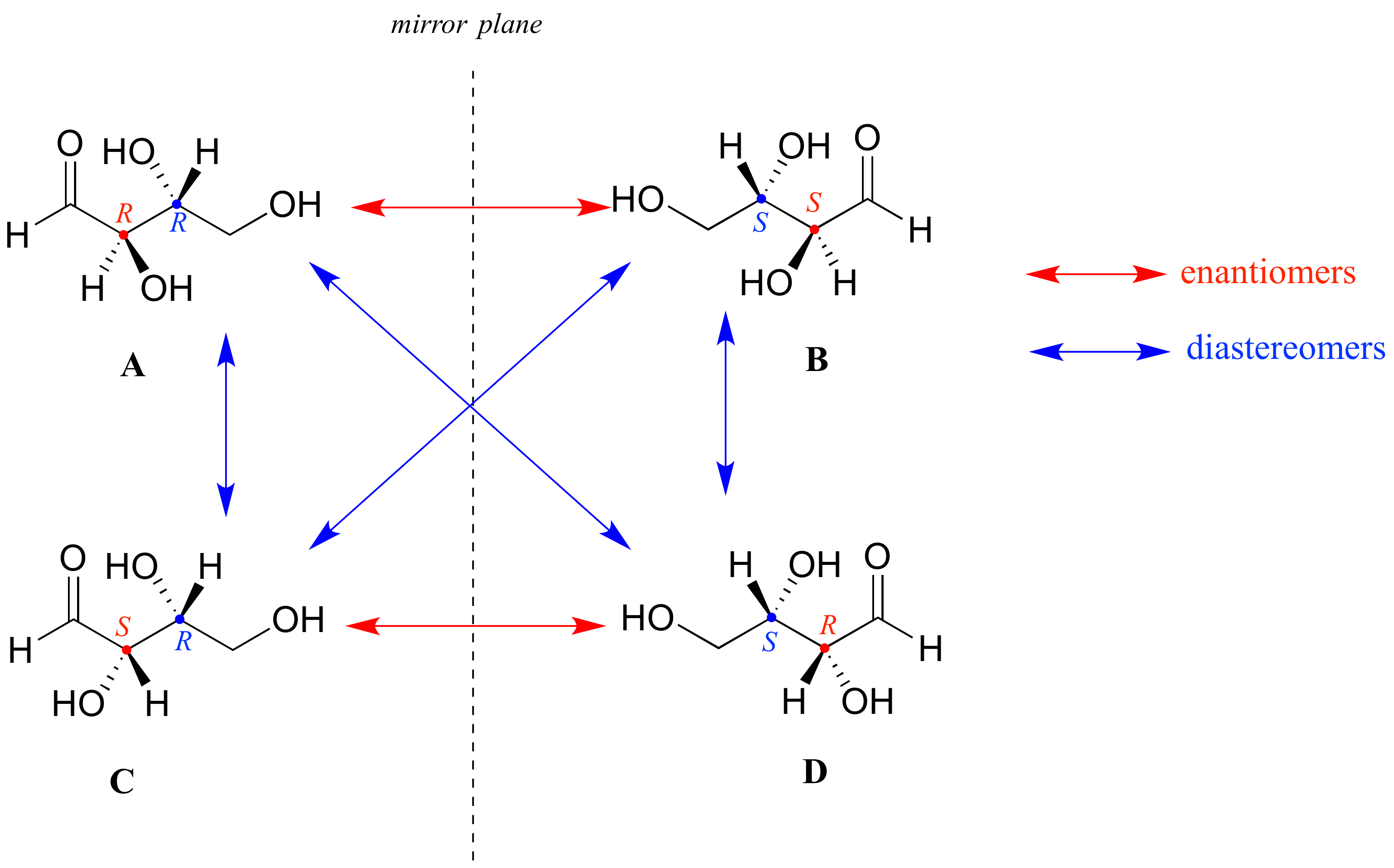
Now, look at compound C, in which the configuration is S at chiral center 1 and R at chiral center 2. Compounds A and C are stereoisomers: they have the same molecular formula and the same bond connectivity, but a different arrangement of atoms in space (recall that this is the definition of the term ‘stereoisomer). However, they are not mirror images of each other (confirm this with your models!), and so they are not enantiomers. By definition, they are diastereomers of each other.

Notice that compounds C and B also have a diastereomeric relationship, by the same definition.

So, compounds A and B are a pair of enantiomers, and compound C is a diastereomer of both of them. Does compound C have its own enantiomer? Compound D is the mirror image of compound C, and the two are not superimposable. Therefore, C and D are a pair of enantiomers. Compound D is also a diastereomer of compounds A and B.

This can also seem very confusing at first, but there some simple shortcuts to analyzing stereoisomers:

Stereoisomer shortcuts

If all of the chiral centers are of opposite R/S configuration between two stereoisomers, they are enantiomers.

If at least one, but not all of the chiral centers are opposite between two stereoisomers, they are diastereomers.

(Note: these shortcuts to not take into account the possibility of additional stereoisomers due to alkene groups)

Here’s another way of looking at the four stereoisomers, where one chiral center is associated with red and the other blue. Pairs of enantiomers are stacked together.

We know, using the shortcut above, that the enantiomer of RR must be SS – both chiral centers are different. We also know that RS and SR are diastereomers of RR, because in each case one – but not both – chiral centers are different.

Meso forms

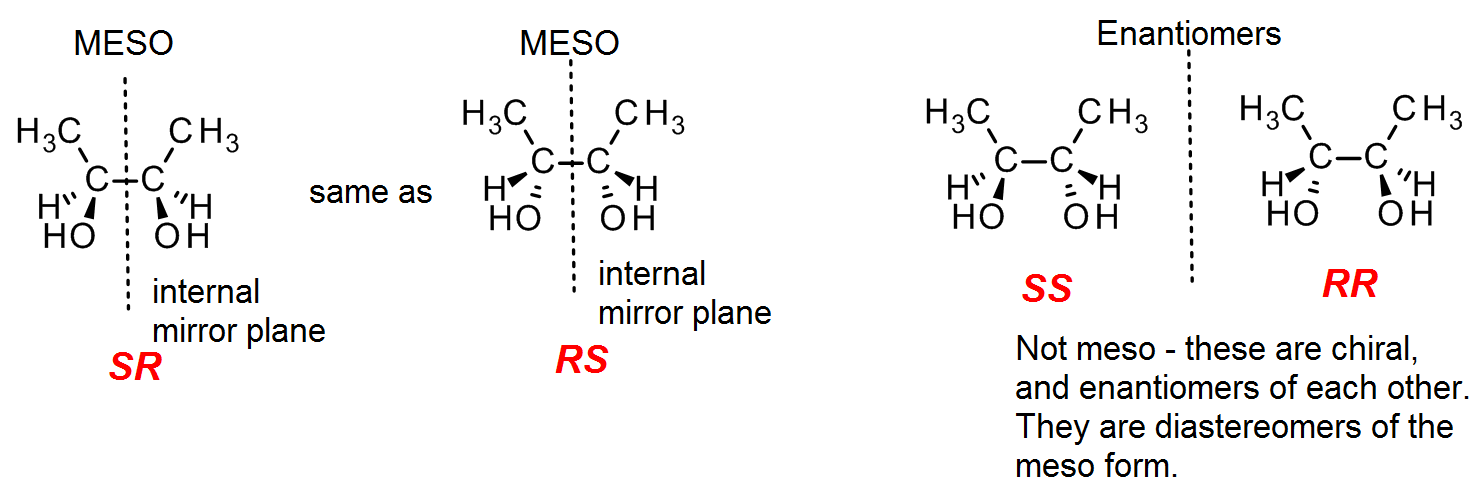
If the two chiral centers in a molecule contain the same four groups, then it is possible that one center is just an “internal reflection” of the other. (Since the groups are the same, we will color both of them red when we indicate R/S.) This produces an internal mirror plane, which means that the overall molecule is achiral (despite the two chiral centers!). Such forms are referred to as meso. For example, with butane-2,3-diol we may have a stereoisomer where the left hand side of the molecule matches the right hand side, shown as SR in the diagram. We also have a mirror image form which is RS, but if you look carefully you will notice that this is simply the SR isomer flipped upside down. Thus both forms are identical and it (they) is meso.

In addition, there are two chiral stereoisomers – the SS and the RR isomers. These are chiral, and not meso.

More than two chiral centers

Now, let’s extend our analysis to a sugar molecule with three chiral centers. Going through all the possible combinations, we come up with eight total stereoisomers – four pairs of enantiomers.

Let’s draw the RRR stereoisomer. Being careful to draw the wedge bonds correctly so that they match the RRR configurations, we get:

Now, using the above drawing as our model, drawing any other stereoisomer is easy. If we want to draw the enantiomer of RRR, we don’t need to try to visualize the mirror image, we just start with the RRR structure and invert the configuration at every chiral center to get SSS.

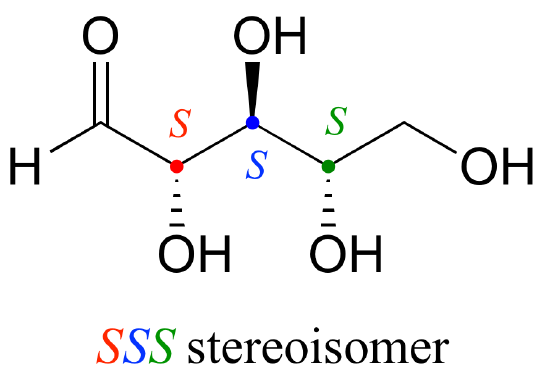
Try making models of RRR and SSS and confirm that they are in fact nonsuperimposable mirror images of each other.

There are six diastereomers of RRR. To draw one of them, we just invert the configuration of at least one, but not all three, of the chiral centers. Let’s invert the configuration at chiral center 1 and 2, but leave chiral center 3 unchanged. This gives us the SSR configuration.

One more definition at this point: diastereomers which differ at only a single chiral center are called epimers. For example, RRR and SRR are epimers:

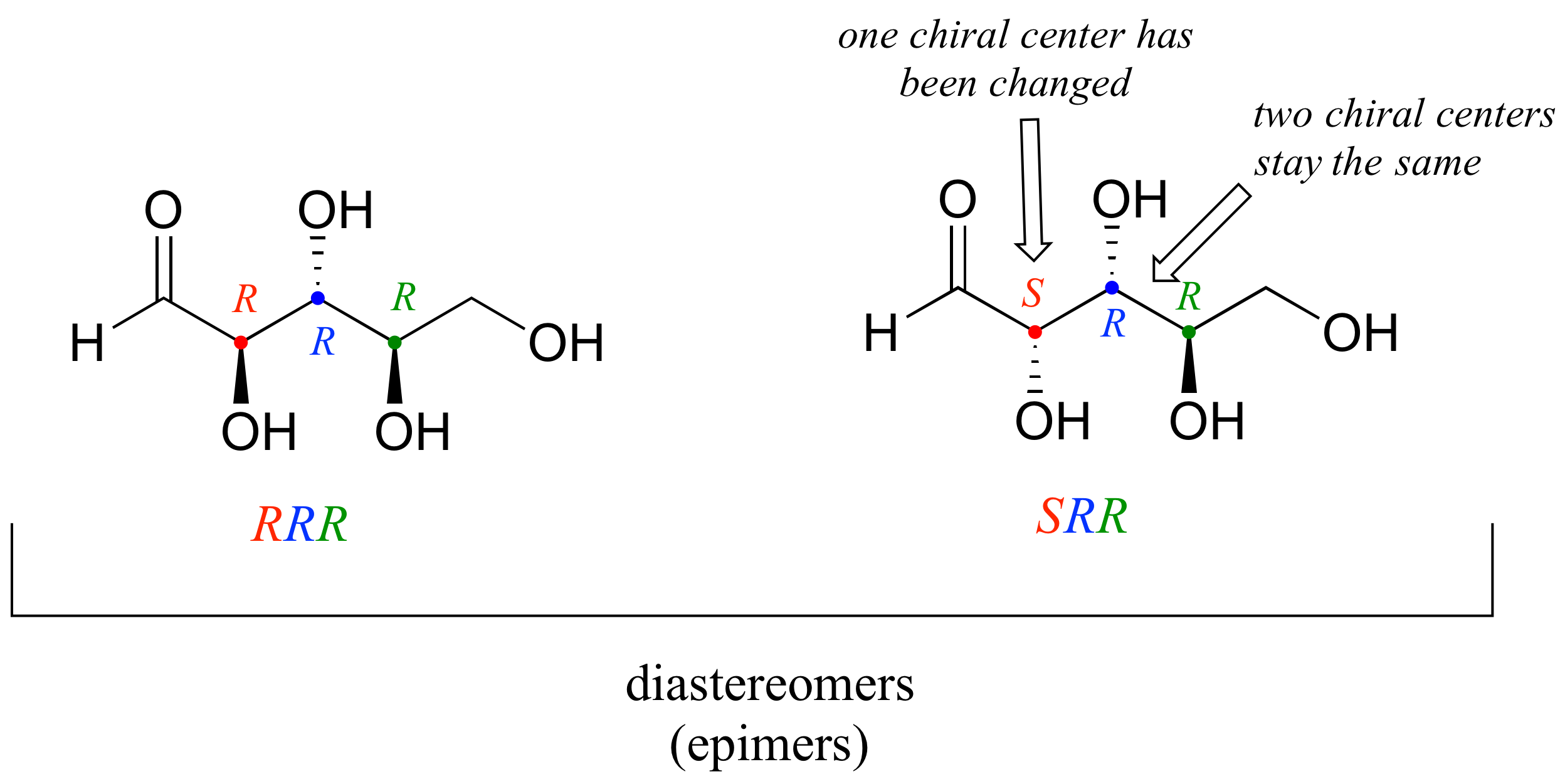
The RRR and SSR stereoisomers shown earlier are diastereomers but not epimers because they differ at two of the three chiral centers.

Exercise

1. a) Draw the structure of the enantiomer of the SRS stereoisomer of the sugar used in the previous example.

b) List (using the XXX format, not drawing the structures) all of the epimers of SRS.

c) List all of the stereoisomers that are diastereomers, but not epimers, of SRS.

[reveal-answer q=”591622″]Show Solution[/reveal-answer]
[hidden-answer a=”591622″]

a) Starting with the RRR stereoisomer (which is given in the example), we flip the first and third chiral center to get SRS. The enantiomer of the SRS stereoisomer is that in which all three chiral centers are flipped: the RSR stereoismer.

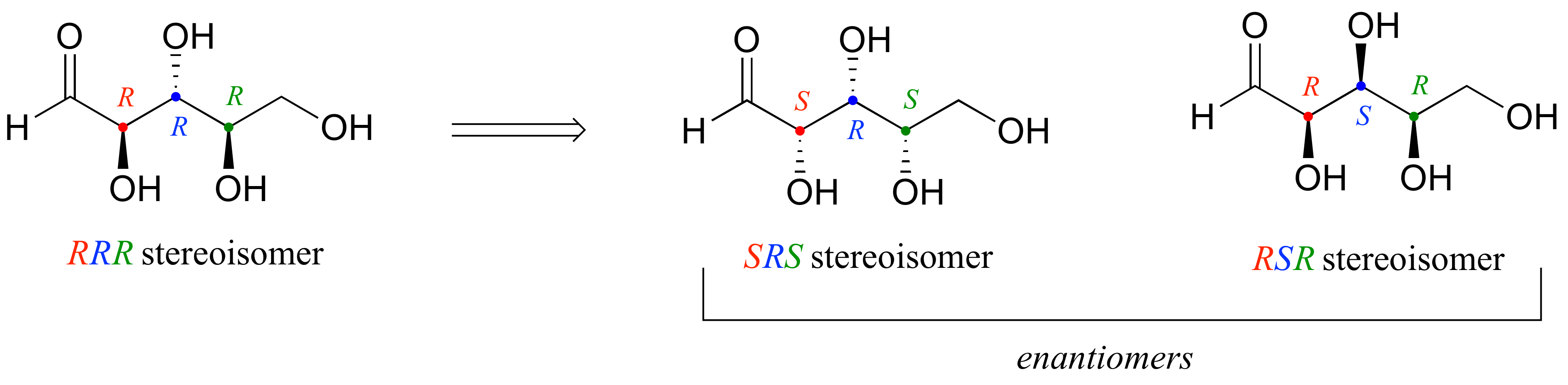
b) Epimers of the SRS stereoismer are RRS, SSS, and SRR (in each case, one of the three chiral centers has been flipped)

c) How to find the compounds that are diastereomers of the SRS stereoisomer, but not epimers? Start with the list of the eight possible stereoisomers given in the example. Cross out SRS itself, and its enantiomer RSR (determined in part (a) above). Then cross out the three epimers we found in part (b). We are left with three isomers: RRR, SSR, and RSS. Each of these have one chiral center in common with SRS, and two that are flipped.

[/hidden-answer]

The epimer term is useful because in biochemical pathways, compounds with multiple chiral centers are isomerized at one specific center by enzymes known as epimerases. Two examples of epimerase-catalyzed reactions are below.

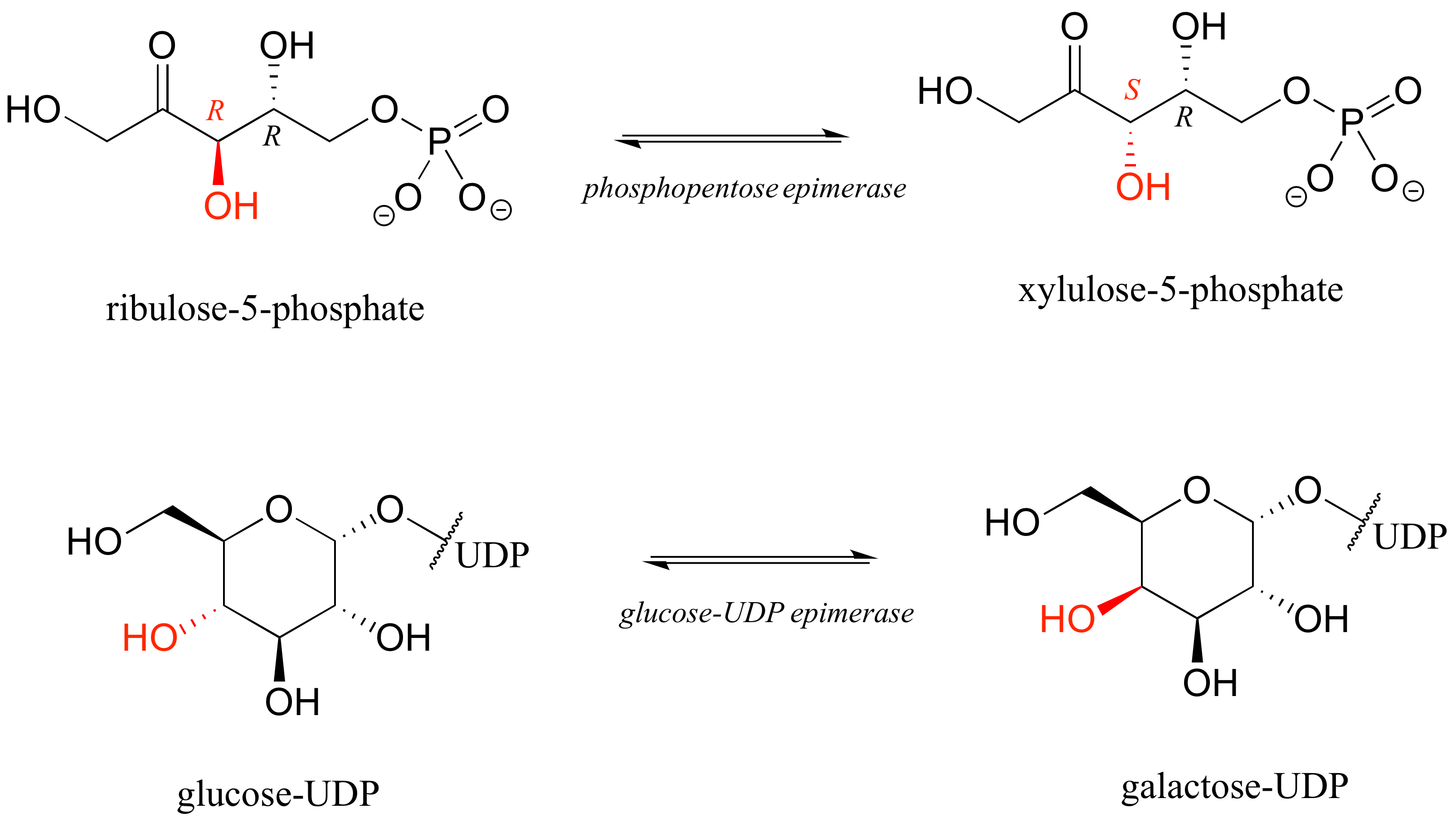
We know that enantiomers have identical physical properties and equal but opposite magnitude specific rotation. Diastereomers, in theory at least, have different physical properties – we stipulate ‘in theory’ because sometimes the physical properties of two or more diastereomers are so similar that it is very difficult to distinguish between them. In addition, the specific rotation values of diastereomers are unrelated – they could be the same sign or opposite signs, similar in magnitude or very dissimilar.

Exercises

1. The sugar below is one of the stereoisomers that we have been discussing.

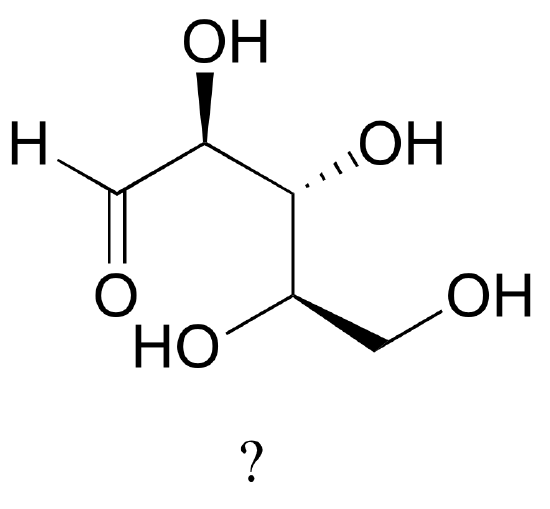
The only problem is, it is drawn with the carbon backbone in a different orientation from what we have seen. Determine the configuration at each chiral center to determine which stereoisomer it is.

[reveal-answer q=”953111″]Show Solution[/reveal-answer]
[hidden-answer a=”953111″]

This is the SRR stereoisomer:

[/hidden-answer]

2. Draw the enantiomer of the xylulose-5-phosphate structure in the previous figure.

[reveal-answer q=”519396″]Show Solution[/reveal-answer]
[hidden-answer a=”519396″]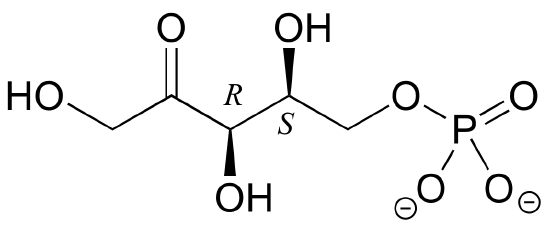[/hidden-answer]

3. The structure of the amino acid D-threonine, drawn without stereochemistry, is shown below. D-threonine has the (S) configuration at both of its chiral centers. Draw D-threonine, it’s enantiomer, and its two diastereomers.

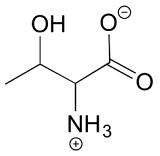
[reveal-answer q=”944385″]Show Solution[/reveal-answer]
[hidden-answer a=”944385″]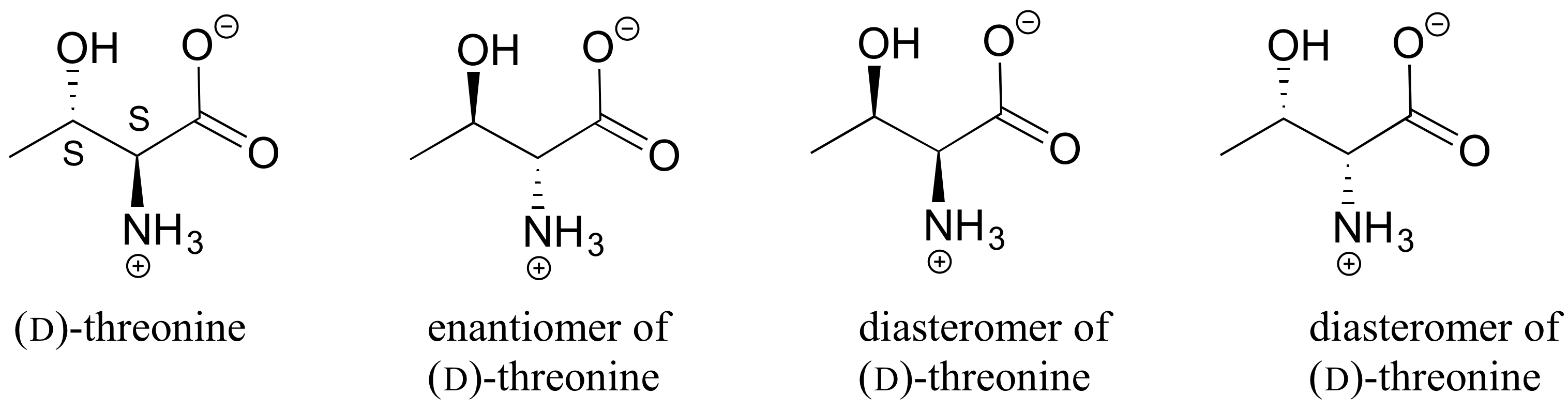[/hidden-answer]

Here is some more practice in identifying isomeric relationships. D-glucose is the monosaccharide that serves as the entrance point for the glycolysis pathway and as a building block for the carbohydrate biopolymers starch and cellulose. The open-chain structure of the sugar is shown below.

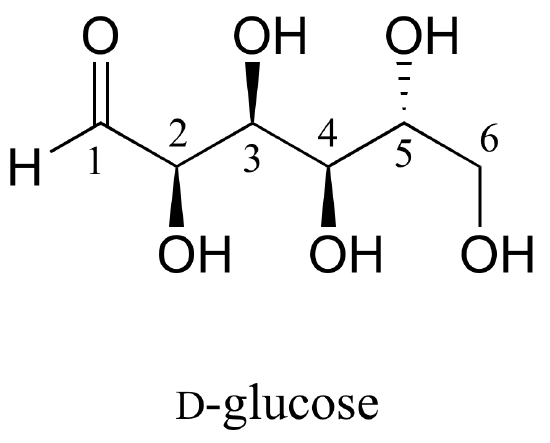
Because D-glucose has four chiral centers, it can exist in a total of 2⁴ = 16 different stereoisomeric forms: it has one enantiomer and 14 diastereomers.

Now, let’s compare the structures of the two sugars D-glucose and D-gulose, and try to determine their relationship.

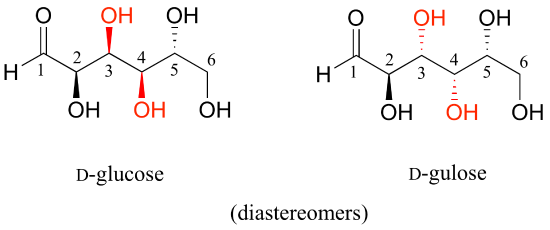
The two structures have the same molecular formula and the same connectivity, therefore they must be stereoisomers. They each have four chiral centers, and the configuration is different at two of these centers (at carbons #3 and #4). They are diastereomers.

Now, look at the structures of D-glucose and D-mannose.

Here, everything is the same except for the configuration of the chiral center at carbon #2. The two sugars differ at only one of the four chiral centers, so again they are diastereomers, and more specifically they are epimers.

D-glucose and L-glucose are enantiomers, because they differ at all four chiral centers.

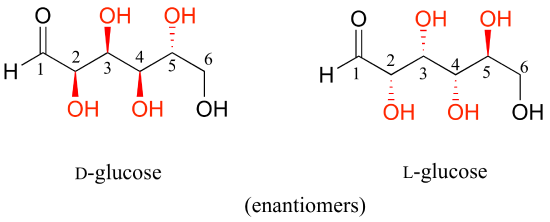
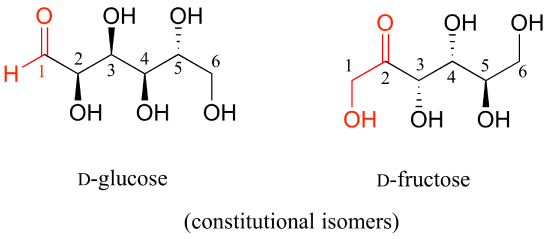
D-glucose is the enantiomer commonly found in nature. D-glucose and D-fructose are not stereoisomers, because they have different bonding connectivity: glucose has an aldehyde group, while fructose has a ketone. The two sugars do, however, have the same molecular formula, so by definition they are constitutional isomers.

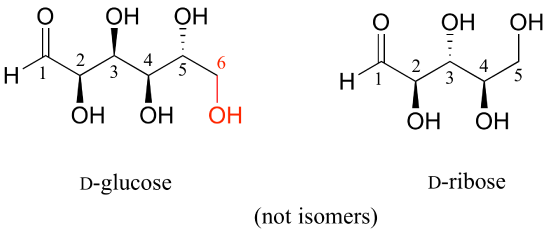
D-glucose and D-ribose are not isomers of any kind, because they have different molecular formulas.

Exercises

1. Identify the relationship between each pair of structures. Your choices are: not isomers, constitutional isomers, diastereomers but not epimers, epimers, enantiomers, or same molecule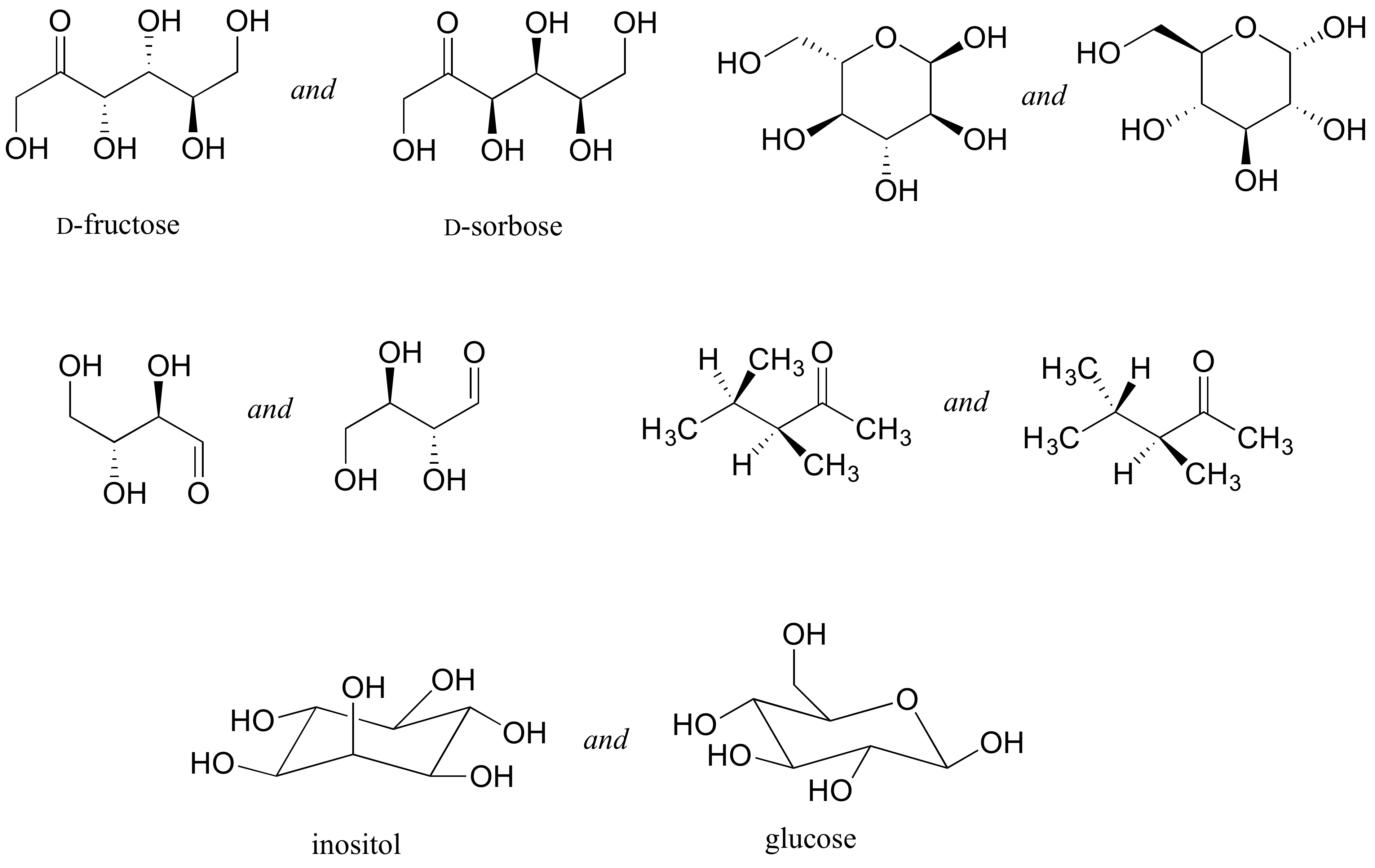
[reveal-answer q=”29238″]Show Solution[/reveal-answer]
[hidden-answer a=”29238″]Going left to right, top to bottom:

Diastereomers (two chiral centers are flipped).

Enantiomers (all five chiral centers are flipped).

Identical (drawing is flipped vertically but they are the same structure).

Identical (the carbon which appears to be flipped in the drawing is not a chiral center).

Constitutional isomers (same molecular formula, but notice that inositol does not have a ring oxygen. Is not a monosaccharide, it is a cyclohexane with six hydroxyl substituents.)

[/hidden-answer]

2. Identify the relationship between each pair of structures. Hint – figure out the configuration of each chiral center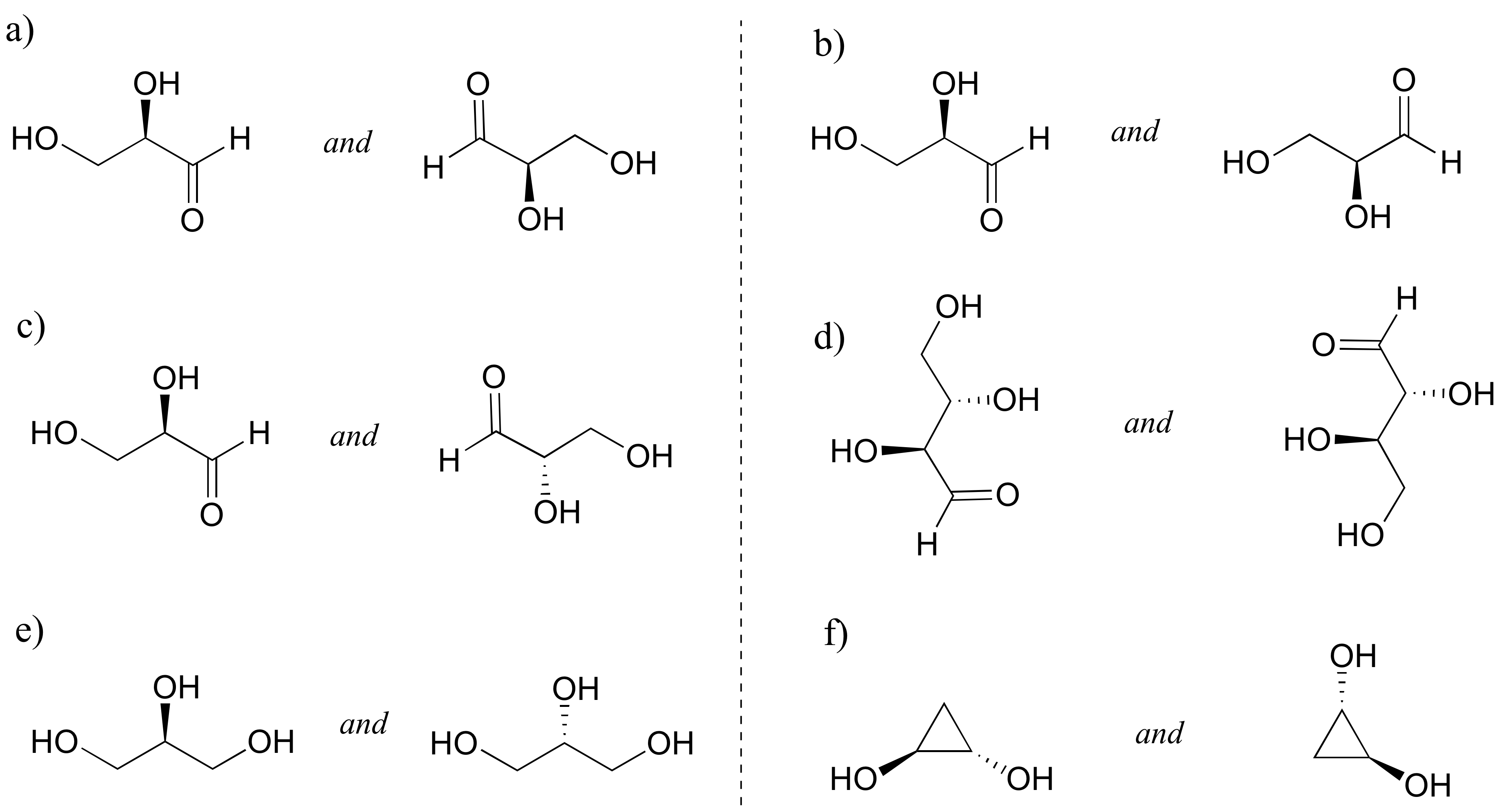[reveal-answer q=”698380″]Show Solution[/reveal-answer]
[hidden-answer a=”698380″]

a) Identical. They have the same molecular formula and connectivity; there is only one chiral center, which is R in both structures.

b) Enantiomers. The compound on the left is R, compound on the right is S.

c) Enantiomers. The compound on the left is R, compound on the right is S.

d) Enantiomers. The compound on the left is SS, compound on the right is RR.

e) Identical. The structures are both glycerol, which is not chiral (the left and right ‘arms’ are the same, so the middle carbon is not a chiral center)

f) Identical. Both structures are SS. Also, notice that if you rotate the right-side structure 120 degrees clockwise, it becomes exactly the same as the left-side structure.[/hidden-answer]

Khan Academy video tutorial on stereoisomeric relationships