5.10: Adding Geogebra Explorations to LibreTexts Pages
- Page ID
- 394382
Adding interactive problems/activities using can make your LibreTexts more interactive and provide immediate feedback to students on their understanding. In addition to interactive problems from H5P, WeBWorK, or MyOpenMath, you can easily also add GeoGebra explorations to your LibreTexts.
Although GeoGebra Explorations are not included as a problem type in Adapt, there are some existing GeoGebra explorations in the LibreTexts Math Library (https://math.libretexts.org/Learning_Objects/GeoGebra_Simulations). It is also fairly easy to find existing GeoGebra explorations addressing many topics using a search engine or searching on the GeoGebra website (https://www.geogebra.org/). If nothing you find demonstrates the concept(s) you have in mind, it's not too hard to learn to create your own GeoGebra explorations using GeoGebra Classic on the web.
In this tutorial, we will learn how to insert GeoGebra explorations in a Libretexts page. There are several ways to to this. The process you need depends on whether the GeoGebra exploration you want to insert is found in a LibreTexts respository or if you found it (or created it) on the GeoGebra website.
We'll cover how to insert an existing GeoGebra exploration from a LibreTexts repository first and then cover how to insert any GeoGebra exploration you find or create online.
Inserting GeoGebra Explorations from a LibreTexts Repository
The GeoGebra exploration below comes from the collection of GeoGebra explorations in the repository mentioned above on the LibreTexts Math Library.
Frenet Frame GeoGebra Exploration
To add this GeoGebra exploration to this page, you would first need to locate it by name on the repository page described above. Then Edit the LibreTexts page where you wish to insert it. Next select the Elements option shown along the top bar of the page editing window, and on the Elements menu, select the Content reuse option (shown in Figure \(\PageIndex{1}\)).
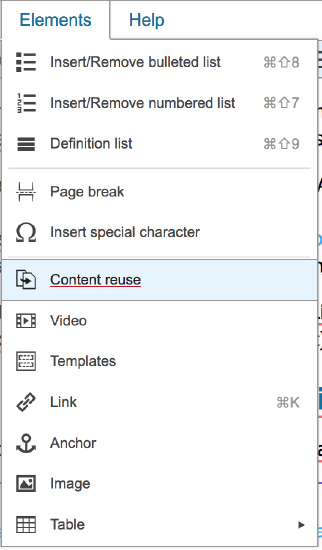Figure \(\PageIndex{1}\): Elements menu, showing Content reuse option
Selecting the Content reuse option allows us to add content from anywhere else in the library. You will see the following window (shown in Figure \(\PageIndex{2}\)).
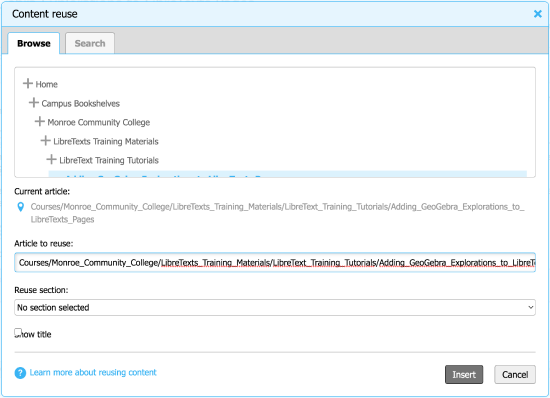Figure \(\PageIndex{2}\): The Content reuse dialog
To navigate to the Learning Objects folder, click on the plus symbol in front of the word Home. The list of folders should now appear like Figure \(\PageIndex{3}\) below.
Figure \(\PageIndex{3}\): List of folders shown when we click the plus symbol in front of Home
Now click on the plus symbol in front of Learning Objects should display a list similar to that shown below in Figure \(\PageIndex{4}\).
Figure \(\PageIndex{4}\): A list of available Learning Objects
Clicking the plus sign in front of GeoGebra Simulations should reveal a list of the current GeoGebra explorations in this repository. Scrolling down to locate the Frenet Frame exploration, it should look similar to what is shown in Figure \(\PageIndex{5}\).
Figure \(\PageIndex{5}\): A list of available GeoGebra explorations
Selecting the Frenet Frame exploration causes the Content reuse dialog to appear as shown below in Figure \(\PageIndex{6}\).
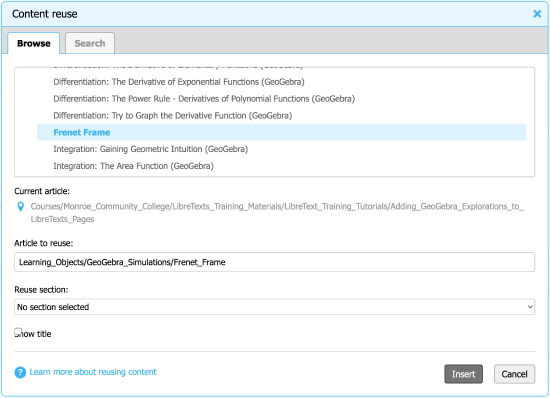Figure \(\PageIndex{6}\): The Frenet Frame exploration has been selected
Note the address of the Frenet Frame exploration within the LibreTexts Math Library is shown under Article to reuse. If you select the checkbox labeled Show title, the title of the exploration will be automatically displayed just above the exploration on your page. If this checkbox is left unselected, this title will not appear.
Finally, once you are ready to insert the exploration into your page, click the Insert button in the lower-right corner of the dialog. A content reuse placeholder like the following will appear in the page editing window. To see your inserted GeoGebra exploration in action, save the page.
Figure \(\PageIndex{7}\): Placeholder for the content reuse of the Frenet Frame GeoGebra exploration
Inserting GeoGebra Explorations from a Different LibreTexts Library
If you decide you'd like to insert a GeoGebra exploration from a LibreTexts library other than the one in which you are building your custom text, this can be accomplished using a Cross-Library Reference, the library subject area, and the Page ID number for the GeoGebra exploration you have selected.
Say we wish to insert the following GeoGebra exploration from the LibreTexts Math Library on a page in another LibreTexts library (say Chemistry or Physics).
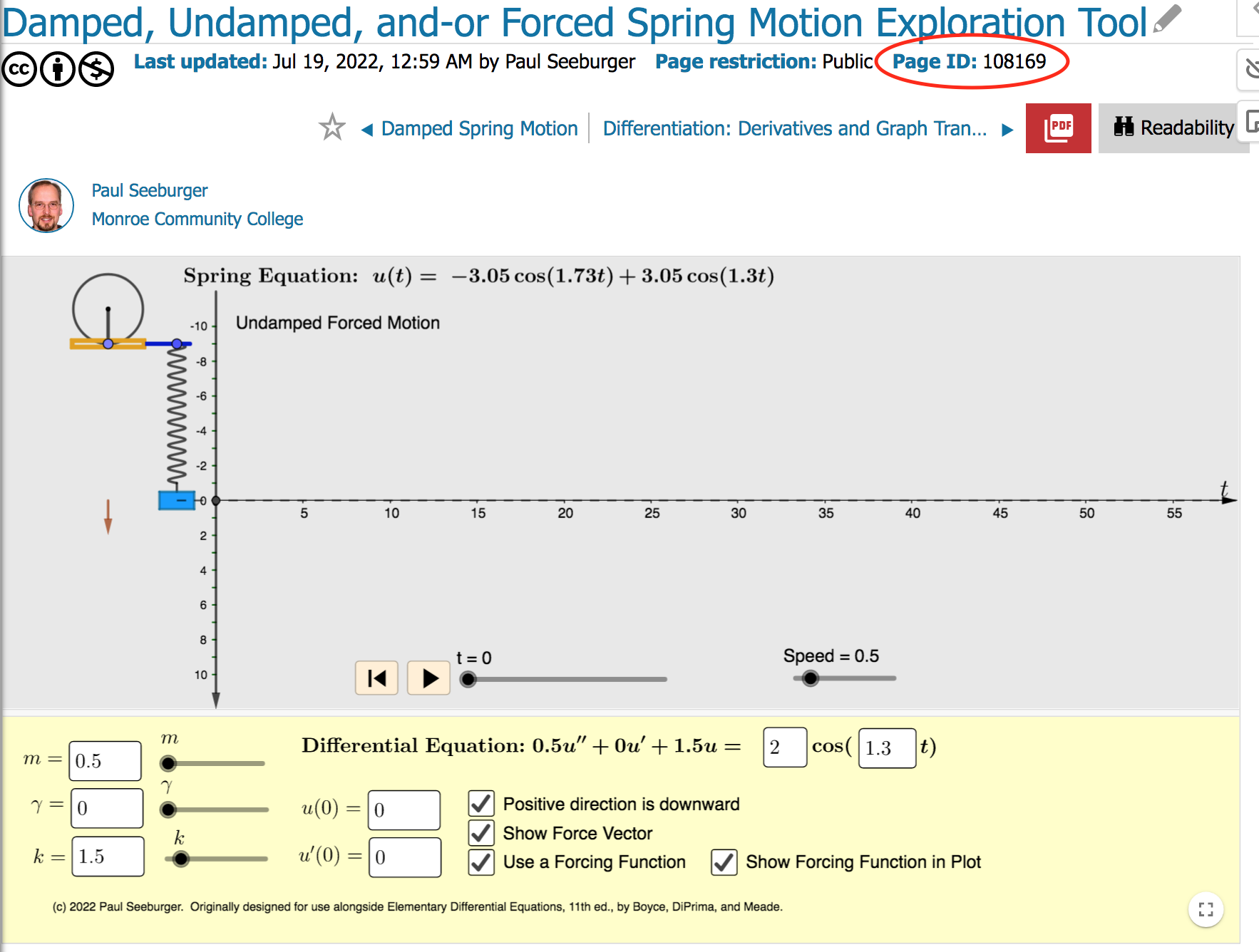Figure \(\PageIndex{6}\): Static image of a GeoGebra exploration from the LibreTexts Math Library, with its Page ID circled in red.
We would need to create a new page, name it, and then save it (before editing it) to set it up with the correct codes. Then we would edit the page again and click on the </> HTML button on the right end of the editing toolbar. Enter the following code.
<p class="mt-script-comment">Cross Library Transclusion</p>
<pre class="script">
template('CrossTransclude/Web',{'Library':'math','PageID':108169});</pre>
Saving your page should reveal the GeoGebra exploration you wanted. This code could also be placed inside a LibreTexts page with other text and figures, or you could set up a collection of explorations each in their own page that you could easily place in other pages using the Content Reuse approach described above.
This Cross Library Transclusion code can be used to insert any content from another library into your custom LibreTexts.
Inserting GeoGebra Explorations from the GeoGebra Website
First go to the GeoGebra website (https://www.geogebra.org/) and locate an exploration that you would like to insert into LibreTexts. If you've created one of your own, feel free to use that! You'll just need the URL of this exploration when we are ready to indicate which exploration we want to insert below.
There are a lot of more advanced programming features that can be used in this process. But for most purposes, we will not need to get this complicated to insert an interactive GeoGebra exploration in a LibreText, so I will not get into these more advanced techniques here.
If you are curious to learn more about how some of the GeoGebra explorations in the repository are set up, you copy the GeoGebra exploration from the repository to your sandbox (either using the remixer or creating a new page and then using content reuse) and then fork the page. This will allow you to explore the code needed to accomplish using buttons and text output displays that are external to a single GeoGebra exploration window or to coordinate two separate GeoGebra applet windows.
Although a GeoGebra exploration likely could be inserted directly into a LibreTexts page with other content, I strongly recommend that you create a new (separate) page for each GeoGebra exploration you wish to insert, in a subdirectory of your campus bookshelf dedicated to GeoGebra explorations (perhaps titled GeoGebra Explorations) and then use the content reuse approach shown above to locate and insert these explorations into your page. This approach keeps the code for each GeoGebra exploration clearly separate and allows these explorations to be more easily shared among multiple books once they have been created.
This approach also provides an excellent template to use for creating more GeoGebra exploration pages for your LibreTexts. Once you have one of these created, you can just use the Copy option under the Options menu on the page to create a new GeoGebra exploration page. There will be no need to fork the page. You'll just have to edit the code as shown below.
The first time (to get started), I recommend that you copy one of the following GeoGebra explorations from the repository into a page of your own.
Accumulation Function Curve Sketching Example 1 or Accumulation Function Exploration Tool
You can use the Remixer to do this or you can create a new page using the New button and use Content reuse (as described above) to insert just this exploration into the page.
Note that if you create a new page using the New button, you should always name and save the page first, then edit it again to add content or use Content reuse (as we need to do to insert the existing exploration above). This maintains the tags that indicate that this page is a section.
Once you have the copy of the exploration in your page, save it and then fork it, either clicking on the fork symbol just to the right of the title (if it is there), or using the Forker option in the Options menu.
Edit the page and click on the HTML button. You will see code like the following:
<meta name="viewport" content="width=device-width,initial-scale=1" /><meta charset="utf-8" /><script src="https://www.geogebra.org/apps/deployggb.js"></script>
<div id="ggb-element"> </div>
<script>/*<![CDATA[*/
var params = {"appName": "classic", "material_id":"vy5cfdug", "width": 1260, "height": 657, "scale": 0.90, "showToolBar": false, "showAlgebraInput": false, "showMenuBar": false, "showFullscreenButton": true };
var applet = new GGBApplet(params, true);
window.addEventListener("load", function() {
applet.inject('ggb-element');
});
/*]]>*/</script>
If you used the remixer or content reuse to create the page and then forked the page, you will likely also see some comment code that you can freely delete, possibly both above and below the code shown above.
Now find a GeoGebra exploration that you want to insert. Its web address (URL) should look something like the following:
https://www.geogebra.org/m/ykqc5be6
Note that the material id for this exploration is the sequence of letters and numbers after the base URL: https://www.geogebra.org/m/. That is, in this case, the material id is ykqc5be6.
Copy just this material id code and paste it in the parentheses following "material_id", replacing the current material id. (In the example code above, this code is "vy5cfdug".)
Save the page and you will see your new exploration appear. You may need to adjust the width and height settings to allow all parts of the exploration to appear, and you can experiment with the other settings shown in the code above on the line beginning with "var params =".
Be sure to clearly indicate who authored the GeoGebra exploration that you have imported, if it is not already displayed. It is best to include it just below the exploration on its own page.
Now that you have your new GeoGebra exploration in its own LibreTexts page on your campus bookshelf, you can use the content reuse approach described in the first part of this tutorial to insert this GeoGebra exploration into a regular LibreText textbook page. To do this, you will need to navigate to your campus bookshelf using the Content reuse dialog.