3.4.1. Newman Projections
- Page ID
- 33759
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Before we begin our exploration of stereochemistry and chirality, we first need to consider the subject of conformational isomerism, which has to do with rotation about single bonds.
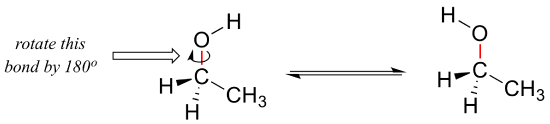
We learned in section 2.1 that single bonds in organic molecules are free to rotate, due to the 'end-to-end' (sigma) nature of their orbital overlap. Consider the carbon-oxygen bond in ethanol, for example: with a 180o rotation about this bond, the shape of the molecule would look quite different:
Or ethane: rotation about the carbon-carbon sigma bond results in many different possible three-dimensional arrangements of the atoms.

These different arrangements, resulting from sigma bond rotation, are referred to in organic chemistry as conformations. Any one specific conformation is called a conformational isomer, or conformer.
In order to better visualize different conformations of a molecule, it is convenient to use a drawing convention called the Newman projection. In a Newman projection, we look lengthwise down a specific bond of interest – in this case, the carbon-carbon bond in ethane. We depict the ‘front’ atom as a dot, and the ‘back’ atom as a larger circle.

The six carbon-hydrogen bonds are shown as solid lines protruding from the two carbons. Note that we do not draw bonds as solid or dashed wedges in a Newman projection.
Looking down the C-C bond in this way, the angle formed between a C-H bond on the front carbon and a C-H bond on the back carbon is referred to as a dihedral angle. (The dihedral angle between the hour hand and the minute hand on a clock is 0o at noon, 90o at 3:00, and so forth).
The lowest energy conformation of ethane, shown in the figure above, is called the ‘staggered’ conformation: all of the dihedral angles are 60o, and the distance between the front and back C-H bonds is maximized.
If we now rotate the front CH3 group 60° clockwise, the molecule is in the highest energy ‘eclipsed' conformation, where the dihedral angles are all 0o (we stagger the bonds slightly in our Newman projection drawing so that we can see them all).

The energy of the eclipsed conformation, where the electrons in the front and back C-H bonds are closer together, is approximately 12 kJ/mol higher than that of the staggered conformation.
Another 60° rotation returns the molecule to a second staggered conformation. This process can be continued all around the 360° circle, with three possible eclipsed conformations and three staggered conformations, in addition to an infinite number of conformations in between these two extremes.
Now let's consider butane, with its four-carbon chain. There are now three rotating carbon-carbon bonds to consider, but we will focus on the middle bond between C2 and C3. Below are two representations of butane in a conformation which puts the two CH3 groups (C1 and C4) in the eclipsed position, with the two C-C bonds at a 0o dihedral angle.
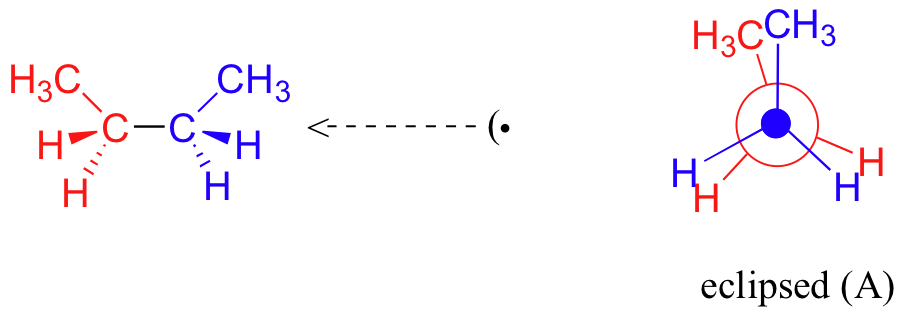
If we rotate the front, (blue) carbon by 60° clockwise, the butane molecule is now in a staggered conformation.
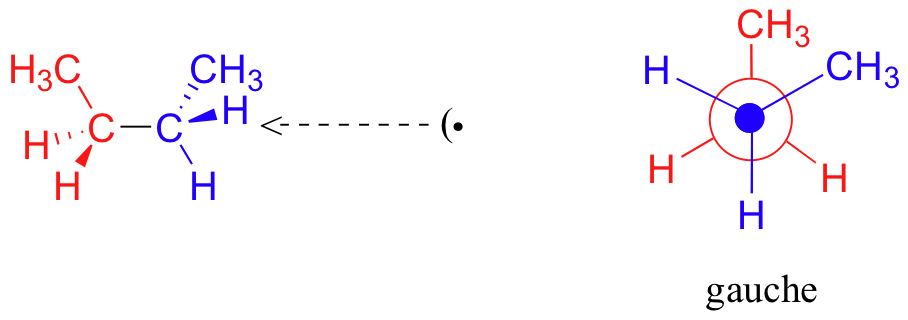
This is more specifically referred to as the gauche conformation of butane. Notice that although they are staggered, the two methyl groups are not as far apart as they could possibly be.
A further rotation of 60° gives us a second eclipsed conformation (B) in which both methyl groups are lined up with hydrogen atoms.
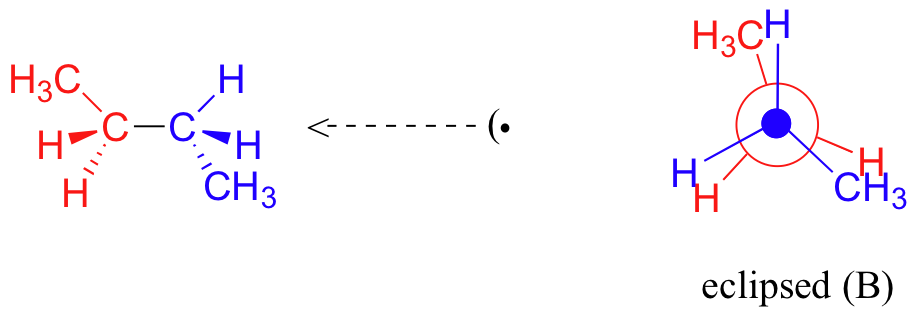
One more 60 rotation produces another staggered conformation called the anti conformation, where the two methyl groups are positioned opposite each other (a dihedral angle of 180o).
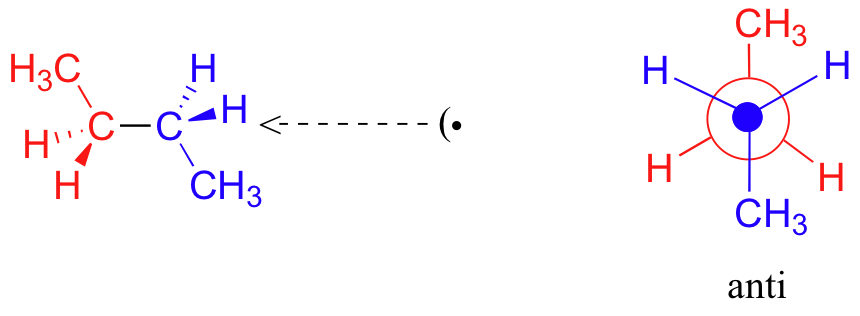
As with ethane, the staggered conformations of butane are energy 'valleys', and the eclipsed conformations are energy 'peaks'. However, in the case of butane there are two different valleys, and two different peaks. The gauche conformation is a higher energy valley than the anti conformation due to steric strain, which is the repulsive interaction caused by the two bulky methyl groups being forced too close together. Clearly, steric strain is lower in the anti conformation. In the same way, steric strain causes the eclipsed A conformation - where the two methyl groups are as close together as they can possibly be - to be higher in energy than the two eclipsed B conformations.
The diagram below summarizes the relative energies for the various eclipsed, staggered, and gauche conformations.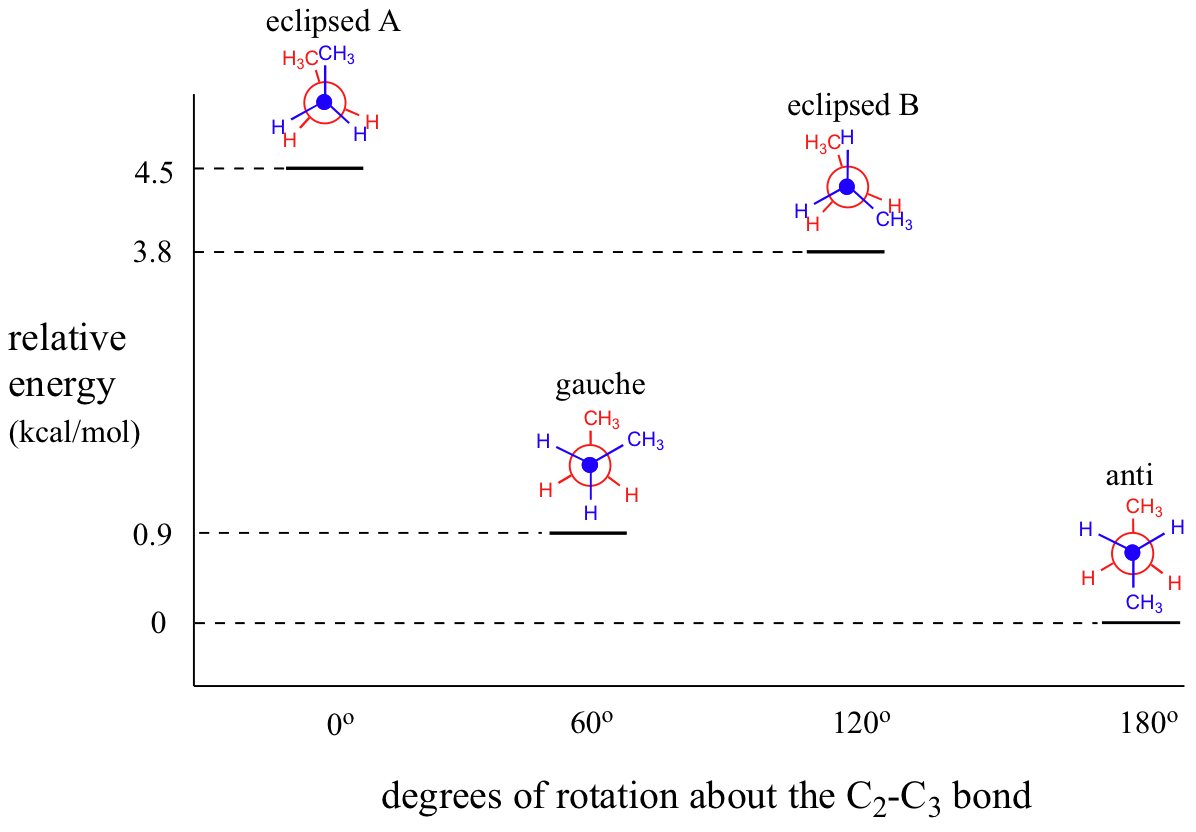
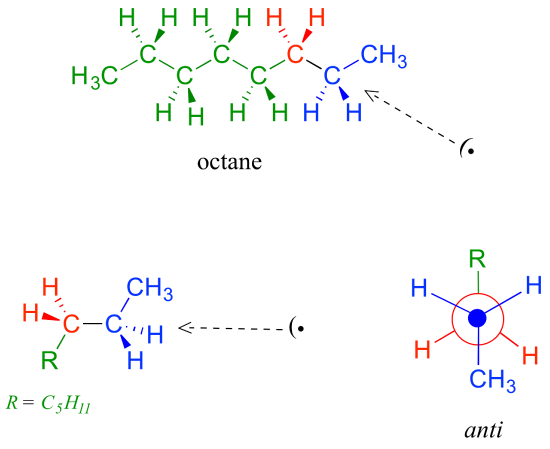
Because the anti conformation is lowest in energy (and also simply for ease of drawing), it is conventional to draw open-chain alkanes in a 'zigzag' form, which implies anti conformation at all carbon-carbon bonds. The figure below shows, as an example, a Newman projection looking down the C2-C3 bond of octane.
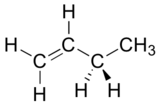
Exercise 3.1: Draw Newman projections of the lowest and highest energy conformations of propane.
Exercise 3.2: Draw a Newman projection, looking down the C2-C3 bond, of 1-butene in the conformation shown below (C2 should be your front carbon).
Online lectures from Kahn Academy
Newman projections part I
Newman projections part II
Further Reading
MasterOrganicChemistry
Carey 4th Edition On-Line Activity
Khan Academy
Leah4Sci
Cliffs Notes
Slide Presentations
Web Pages
Videos
Video on Converting between Newman projections and line structures
drawing Newman projection video
Conformation and Newman projection video
Tutorial
How to Draw Newman Projections
Long Newman projection tutorial
How to draw Newman projections
Switching between Newman projections and dash-wedge drawings
Other tools
Interactive page on Newman projections
Practice Problems
Worksheet with practice problems on newman projections, with answers

