5.3 Nuclear Magnetic Resonance (NMR) Spectroscopy
- Page ID
- 17122
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
Some types of atomic nuclei act as though they spin on their axis similar to the Earth. Since they are positively charged they generate an electromagnetic field just as the Earth does. So, in effect, they will act as tiny bar magnetics. Not all nuclei act this way, but fortunately both 1H and 13C do have nuclear spins and will respond to this technique.

NMR Spectrometer
In the absence of an external magnetic field the direction of the spin of the nuclei will be randomly oriented (see figure below left). However, when a sample of these nuclei is place in an external magnetic field, the nuclear spins will adopt specific orientations much as a compass needle responses to the Earth’s magnetic field and aligns with it. Two possible orientations are possible, with the external field (i.e. parallel to and in the same direction as the external field) or against the field (i.e. antiparallel to the external field). See figure below right.
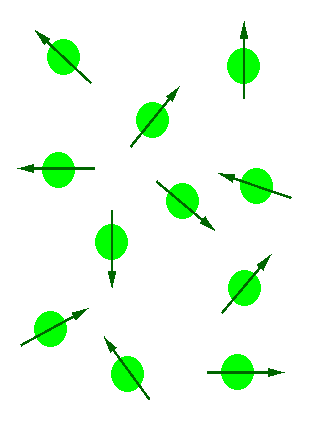
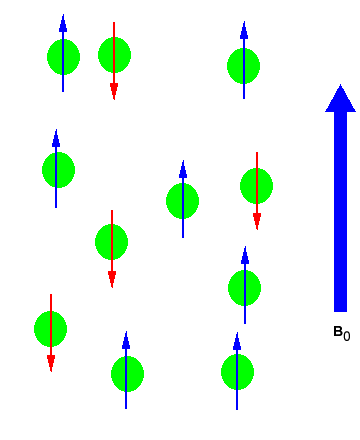
Figure 1: (Left) Random nuclear spin without an external magnetic field. (Right)Ordered nuclear spin in an external magnetic field
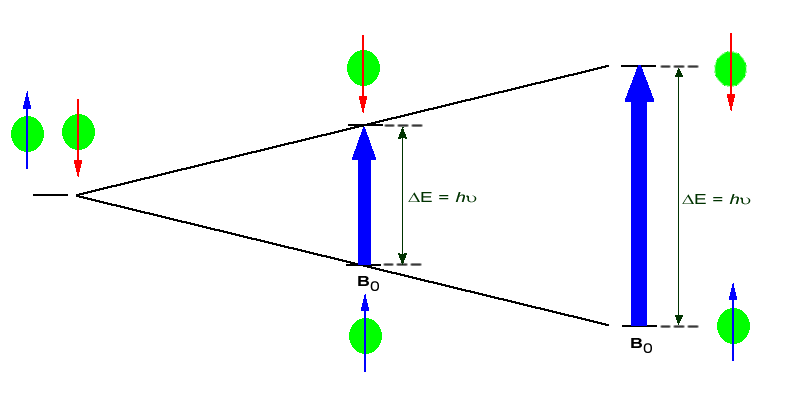
If the ordered nuclei are now subjected to EM radiation of the proper frequency the nuclei aligned with the field will absorb energy and "spin-flip" to align themselves against the field, a higher energy state. When this spin-flip occurs the nuclei are said to be in "resonance" with the field, hence the name for the technique, Nuclear Magentic Resonance or NMR.
The amount of energy, and hence the exact frequency of EM radiation required for resonance to occur is dependent on both the strength of the magnetic field applied and the type of the nuclei being studied. As the strength of the magnetic field increases the energy difference between the two spin states increases and a higher frequency (more energy) EM radiation needs to be applied to achieve a spin-flip (see image below).
Superconducting magnets can be used to produce very strong magnetic field, on the order of 21 tesla (T). Lower field strengths can also be used, in the range of 4 - 7 T. At these levels the energy required to bring the nuclei into resonance is in the MHz range and corresponds to radio wavelength energies, i.e. at a field strength of 4.7 T 200 MHz bring 1H nuclei into resonance and 50 MHz bring 13C into resonance. This is considerably less energy then is required for IR spectroscopy, ~10-4 kJ/mol versus ~5 - ~50 kJ/mol.
1H and 13C are not unique in their ability to undergo NMR. All nuclei with an odd number of protons (1H, 2H, 14N, 19F, 31P ...) or nuclei with an odd number of neutrons (i.e. 13C) show the magnetic properties required for NMR. Only nuclei with even number of both protons and neutrons (12C and 16O) do not have the required magnetic properties.
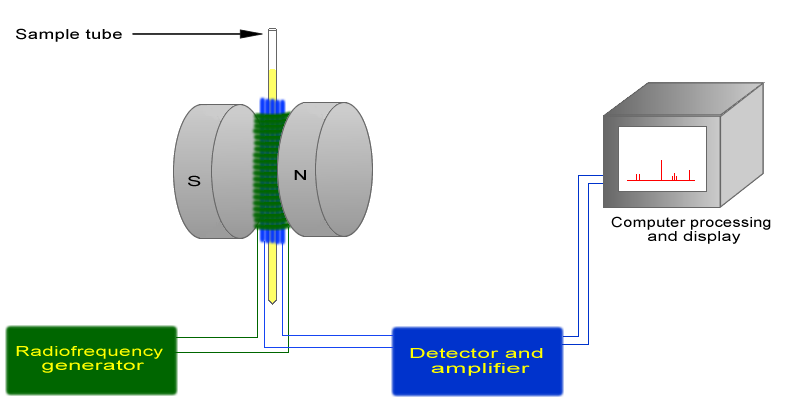
The basic arrangement of an NMR spectrometer is displayed below. A sample (in a small glass tube) is placed between the poles of a strong magnetic. A radio frequency generator pulses the sample and excites the nuclei causing a spin-flip. The spin flip is detected by the detector and the signal sent to a computer where it is processed.
Chemical Shifts
The NMR spectra is displayed as a plot of the applied radio frequency versus the absorption. The applied frequency increases from left to right, thus the left side of the plot is the low field, downfield or deshielded side and the right side of the plot is the high field, upfield or shielded side (see the figure below). The concept of shielding will be explained shortly.
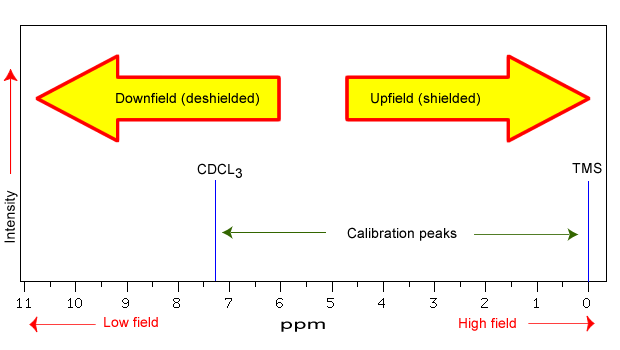
The position on the plot at which the nuclei absorbs is called the chemical shift. Since this has an arbitrary value a standard reference point must be used. The two most common standards are TMS (tetramethylsilane, (Si(CH3)4) which has been assigned a chemical shift of zero, and CDCl3 (deuterochloroform) which has a chemical shift of 7.26 for 1H NMR and 77 for 13C NMR.
The scale is commonly expressed as parts per million (ppm) which is independent of the spectrometer frequency. The scale is the delta (δ) scale.

The range at which most NMR absorptions occur is quite narrow. Almost all 1H absorptions occur downfield within 10 ppm of TMS. For 13C NMR almost all absorptions occurs within 220 ppm downfield of the C atom in TMS.
Shielding in NMR
Structural features of the molecule will have an effect on the exact magnitude of the magnetic field experienced by a particular nucleus. This means that H atoms which have different chemical environments will have different chemical shifts. This is what makes NMR so useful for structure determination in organic chemistry. There are three main features that will affect the shielding of the nucleus, electronegativity, magnetic anisotropy of π systems and hydrogen bonding.
Electronegativity
The electrons that surround the nucleus are in motion so they created their own electromagnetic field. This field opposes the the applied magnetic field and so reduces the field experienced by the nucleus. Thus the electrons are said to shield the nucleus. Since the magnetic field experienced at the nucleus defines the energy difference between spin states it also defines what the chemical shift will be for that nucleus. Electron with-drawing groups can decrease the electron density at the nucleus, deshielding the nucleus and result in a larger chemical shift. Compare the data in the table below.
| Compound, CH3X | CH3F | CH3OH | CH3Cl | CH3Br | CH3I | CH4 | (CH3)4Si |
| Electronegativity of X | 4.0 | 3.5 | 3.1 | 2.8 | 2.5 | 2.1 | 1.8 |
| Chemical shift δ (ppm) | 4.26 | 3.4 | 3.05 | 2.68 | 2.16 | 0.23 | 0 |
As can be seen from the data, as the electronegativity of X increases the chemical shift, δ increases. This is an effect of the halide atom pulling the electron density away from the methyl group. This exposes the nuclei of both the C and H atoms, "deshielding" the nuclei and shifting the peak downfield.
The effects are cumulative so the presence of more electron withdrawing groups will produce a greater deshielding and therefore a larger chemical shift, i.e.
| Compound | CH4 | CH3Cl | CH2Cl2 | CHCl3 |
| δ (ppm) | 0.23 | 3.05 | 5.30 | 7.27 |
These inductive effects are not only felt by the immediately adjacent atoms, but the deshielding can occur further down the chain, i.e.
| NMR signal | -CH2-CH2-CH2Br |
| δ (ppm) | 1.25 1.69 3.30 |
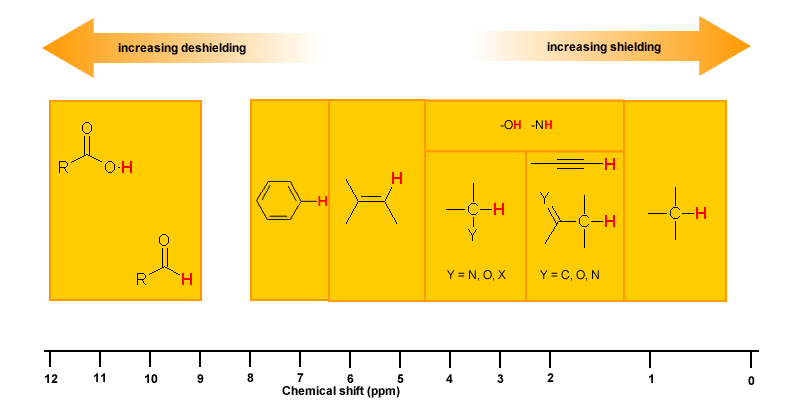
Magnetic Anisotropy: π Electron Effects
The π electrons in a compound, when placed in a magnetic field, will move and generate their own magnetic field. The new magnetic field will have an effect on the shielding of atoms within the field. The best example of this is benzene (see the figure below).

This effect is common for any atoms near a π bond, i.e.
| Proton Type | Effect | Chemical shift (ppm) |
| C6H5-H | highly deshielded | 6.5 - 8 |
| C=C-H | deshielded | 4.5 - 6 |
| C≡C-H | shielded* | ~2.5 |
| O=C-H | very highly deshielded | 9 - 10 |
| * the acetylene H is shielded due to its location relative to the π system | ||
Hydrogen Bonding
Protons that are involved in hydrogen bonding (i.e.-OH or -NH) are usually observed over a wide range of chemical shifts. This is due to the deshielding that occurs in the hydrogen bond. Since hydrogen bonds are dynamic, constantly forming, breaking and forming again, there will be a wide range of hydrogen bonds strengths and consequently a wide range of deshielding. This as well as solvation effects, acidity, concentration and temperature make it very difficult to predict the chemical shifts for these atoms.
Experimentally -OH and -NH can be identified by carrying out a simple D2O exchange experiment since these protons are exchangeable.
- run the normal H-NMR experiment on your sample
- add a few drops of D2O
- re-run the H-NMR experiment
- compare the two spectra and look for peaks that have "disappeared"
H-NMR Chemical Shifts
1H-NMR Spectra
An 1H-NMR will contain a unique signal for each different type of H atom present in the compound. What do we mean by "type" of hydrogen atom? Since the amount of shielding is dependent on the local chemical environment, the exact chemical shift for H atoms can vary widely. There are three basic methods you can use to determine if H atoms are identical.
- Substitution method
This is the simplest but slowest method. The idea is to replace every H atom, one at a time with another atom i.e. a Cl atom to see if you generate a different compound. Each different product indicates a different type of H atom.
- Vebal Description
This requires to you describe each H atom verbally. If you have a different description then the H atoms are different.
For example:- An -NH is differnt from a -CH (based on the atom the H is attached to).
- A -CH3 is different to a -CH2- (based on the number of attached hydrogen atoms).
- An sp3 C-H is different than an sp2 C-H which is different to an sp C-H.
- Others include position on a ring or chain, cis / trans relationships etc.
- Symmetry
The symmetry method is the most sophisticated but requires a knowledge of molecular symmetry. H atoms that are related by mirror planes, axis of rotation or a center of inversion are equivalent to one another.
The first method is the easiet but slowest, the last is the fatest but requires a good knowledge of molecular symmetry. See the thre examples below.
1H-NMR Spectra: Intensity of Signals
There are several important pieces of information that you can obtain from an 1H-NMR. The first is the chemical shift of the peak. This will aid in identifying the type of H atom that produced the signal. The second is the integration ratios of the peaks. The area under a peak of a 1H-NMR is directly proportional to the number of H atoms that produced the peak. The area is calculated by integrating the area, done automatically for you by the software. On older spectra the integration curve was drawn on the spectra, modern software will produce this as a table attached to the spectra. The example below is for methyl t-butyl ether.

The integrals (shown as the red curves) are in a ratio of 333:1000 or 1:3. This implies that the peak on the left corresponds to the methyl group attached to the oxygen (as expected since the O will deshield the H atoms). The peak on the right is the three methyl groups of the t-butyl group, less deshielded as it is further away from the O atom. Note that we get the simplest ratio of H atom types (1:3, methyl : t-butyl) not the true ratio of 3:9.
Spin-Spin Splitting
The NMR above has absorptions which are called singlets, a single sharp peak. However, in most cases, this is not the norm. Absorptions are split into groups of peaks due to coupling between adjacent protons in the molecule.

The 1H-NMR of 1,1,2-tribromoethane is shown above (integration ratios of 10:20 or 1:2). Note that the peaks are now split into a group of two peaks on the right, a doublet and into three peaks on the left, a triplet. The relative areas under the peaks are 1:1 for the doublet, and 1:2:1 for the triplet. The triplet corresponds to the -CHBr2 (most deshielded) proton and the doublet to the -CH2Br (most shielded) protons. This also agrees with the integration.
Spin-spin splitting occurs between unique types of H atoms on the same or adjacent (vicinal) carbon atoms. This occurs because the magnetic fields of each H atom can interact with the magnetic field of other H atoms. The interaction is only important (i.e. leading to spin-spin splitting) when the H atoms are "chemically different" from one another (see preceding page).
Example: Splitting Patterns in 1,1,2-tribromoethane |
|
The methine (-CH-) hydrogen can assume two magnetic spin orientations, with or against the external field. As a result the peak for the adjacent methylene group is split into two lines of equal intensity, a doublet.
The methylene (-CH2-) hydrogen atoms can again assume one of two magnetic spin orientations, with or against the external field. However, in this case these are two H atoms that are identical so there are three possible combinations of their two spins. The first (shown on the left) is both are spin down, the next is both spin up (shown on the right). There are two possible ways for the 1 spin up and 1 spin down combination depending on which specific H atom is spin up or down (shown in the center). The combination produces a triplet with relative intensities of 1:2:1 for the adjacent methine group. |
Example: Splitting Patterns in bromoethane |
|
The 1H-NMR for bromoethane is shown below (integration ratios of 20:30 or 2:3). Note the peaks are now split into a group of three peaks on the right, a triplet and into four peaks on the left, a quartet. The relative areas under the peaks are 1:2:1 for the triplet and 1:3:3:1 for the quartet. The quartet corresponds to the -CH2Br (most deshielded) protons and the triplet corresponds to the -CH3 most sheilded) protons. This also agrees with the integration.  The methylene (-CH2-) hydrogen atoms can assume one of two magnetic spin orientations, with or against the external field. However, in this case these are two H atoms that are identical so there are three possible combinations of their two spins. The first (shown on the left) is both are spin down, the next is both spin up (shown on the right). There are two possible ways for the 1 spin up and 1 spin down combination depending on which specific H atom is spin up or down (shown in the center). The combination produces a triplet with relative intensities of 1:2:1 for the adjacent methyl group.
The methyl (-CH3) hydrogen atoms can again assume one of two magnetic spin orientations, with or against the external field. However in this case there are three protons that are identical so there are four possible combinations of their spins. The most deshielded peak will occur when all three spins are aligned with the field (left most image). The most shielded peak occurs when all three spins are aligned against the field (the right most image). There are now two possibilities left, the case where two spins are with and one against field or two spins against and one with the field. The first case will be mose deshielded than the second case and so downfield form it. This combination will split the adjacent peak for the methylene protons into a quartet with relative intensities of 1:3:3:1.
|
Coupling Constant, J

The coupling constant, (symbol J, units Hz) is a measure of the interaction between a pair of protons.
In a vicinal type of system, Ha-C-C-Hb the coupling between protons Ha and Hb is Jab. The coupling of Hb and Ha must be equal to the coupling between Ha and Hb, of Jab = Jba.
The implications of this is that the spacing betwen the lines for peaks that are coupled must be the same. Compare the peaks from 1,1,2-tribromoethane shown right. This means we can identify which peaks are coupled by the spacing between the lines.
Common Spin Multiplicities
| Number of equivalent adjacent protons |
Multiplicity | Ratio of Intensities |
| 0 | singlet | 1 |
| 1 | doublet | 1:1 |
| 2 | triplet | 1:2:1 |
| 3 | quartet | 1:3:3:1 |
| 4 | quintet | 1:4:6:4:1 |
| 5 | hextet | 1:5:10:10:5:1 |
| 6 | septet | 1:6:15:20:15:6:1 |
Summary
- First, the chemical shift or location of the peak (in ppm) tells you how deshielded the protons are and hence their "local chemical environment", i.e. what possible deshielding groups maybe adjacent to the protons.
- Second, the integration ratios tell you the number of each type of proton in the simplest ratio.
- Third, the spin-spin splitting (coupling pattern or multiplicity) tells you the number of protons on the adjacent C atom. It will be one less than the number of peaks.
- This information combined gives us the basic skeletal structure of the molecule.
Sample 1H-NMR Spectra
| List of Animated 1H-NMR Spectra | ||||||||||
| Bromoethane | 1-bromopropane | 2-propanol | 3-bromopropene | propanal | ||||||
| Phenol | acetone | propanoic acid | ethyl acetate | 2-propenamide | ||||||
| For all spectra click on a peak to highlight the protons responsible for the peak. | ||||||||||
| More spectra can be found at Animated Spectra | ||||||||||
To see the integratals, right click on the spectra to open the menu, go to "view" and check the integrate" box.