3.5 Enantiomers
- Page ID
- 17024
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)An atom with four groups attached to it can also adopt a tetrahedral geometry. This geometry often occurs when the central atom is a little smaller. A tetrahedral geometry allows neighbouring groups to get a little farther from each other.
Unlike square planar compounds, simple tetrahedral compounds do not have the same kind of cis- and trans- isomers. That is, two groups can't be placed on a tetrahedron so that they are opposite each other or beside each other. The relationship between any two groups on a tetrahedron is the same as the relationship between any other two groups on a tetrahedron.
Dichlorodimethylsilane is a compound that can be used to make silicone polymers. Like platin, it has two each of two groups attached to the central atom. However, the central tom is tetrahedral. There is only one way to arrange these four groups.
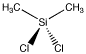
Figure SC3.1. A tetrahedral atom with two different types of groups attached, (CH3)2SiCl2.
However, if four different groups are attached to a tetrahedral atom, the four groups can be arranged in two possible ways. The two compounds that result are mirror images of each other. These two isomers are called enantiomers.
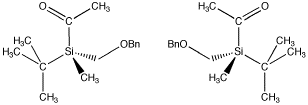
Figure SC3.2. A pair of enantiomers. The (-) enantiomer is on the left and the (+) enantiomer is on the right. Note that the tetrahedral silicon atom has four different groups attached.
- Enantiomers are pairs of compounds with exactly the same connectivity but opposite three-dimensional shapes.
- Enantiomers are not the same as each other; one enantiomer cannot be superimposed on the other.
- Enantiomers are mirror images of each other.
Two compounds with the exact same connectivity, that are mirror images of each other but that are not identical to each other are called enantiomers. The more common definition of an enantiomer is that it is not superimposable on its mirror image. It can be distinguished easily from its mirror image, just as a right hand can easily be identified and distinguished from a left hand.
- Compounds that occur in these pairs are called "chiral".
- "Chiral" comes from the Greek word for "hand".
It can be shown using group theory, the mathematics of symmetry, that an enantiomer may also be defined as a molecule that does not contain a mirror plane, meaning it cannot be divided into two identical and opposite halves.
- Enantiomers contain no mirror planes.
- Enantiomers do not contain two equal and opposite halves.
Unlike cis- and trans-isomers, two enantiomers have the same physical properties. they have the same melting point, the same solubility, and so on. Two compounds that are almost identical, but mirror images of each other, have exactly the same kinds of intermolecular attraction, so it may not be a surprise that their physical properties are identical.
- Enantiomers are another example of a type of stereoisomers.
- Two enantiomers have identical physical properties, except for optical rotation.
Optical rotation involves the interaction of plane-polarized light with a material. If a material is not symmetric, the light that passes through it will be rotated. That means if the waves making up the light are oscillating in one direction as they enter the material, they will have tilted slightly to oscillate in another direction when they emerge from the material. We will look at this phenomenon later.
- Two enantiomers have an equal but opposite rotational effect on plane-polarized light.
- (+) enantiomers rotate light in a clockwise direction.
- (-) enantiomers rotate light in a counterclockwise direction.
For example, in the chiral silicon compound shown above, the (+) enantiomer rotates plane-polarized light in a clockwise direction. It has a "standard optical rotation" of [a] = +12 (+/-2)o. The (-) enantiomer rotates plane-polarized light in a counterclockwise direction. It has a "standard optical rotation" of [a] = -9.9 (+/-2)o.
Problem SC3.1.
A certain compound exists in two forms; enantiomer A and enantiomer B. Enantiomer A has a molecular weight of 126 g/mol, a density of 0.995 g/mL, an optical rotation of [a] = 26o, a melting point of 65 oC, a boiling point of 225 oC, and an odour of citrus fruit. What can you say about the corresponding properties of enantiomer B?
Further Reading on Enantiomers
MasterOrganicChemistry
Carey 4th Edition On-Line Activity
What do I need to Know about Enantiomers?
Khan Academy
Cliffs Notes
Videos
Stereoisomers (Enantiomers) Video
Tutorial