12.2: Radical Reactions
- Page ID
- 365790
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Radical Addition to Alkenes
Recall that electrophilic addition reactions involve the reaction of an alkene with a hydrogen halide (HX) to form the more highly substituted alkyl halide by Markovnikov addition. This proceeds via protonation of the less highly substituted carbon atom of the alkene, formation of a carbocationic intermediate, and SN1-like attack of the atomic p orbital with the nucleophilic halide ion. While this should all seem familiar to you, when this reaction was first discovered, conflicting results were reported. In some cases, especially with HBr additions, the anti-Markovnikov product was generated! We know that this is impossible if the mechanism was truly an electrophilic addition. Well, it turns out that the quality of the HBr played an important role. While fresh bottles of HBr gave the expected Markovnikov product, older bottles of HBr gave the anti-Markovnikov product. It was discovered that older sources of HBr contain small concentrations of peroxides. Since the \(σ\)O-O is weak, there is the potential for generating radicals.
Thus, the mechanism for the radical HBr addition is as follows, and can be divided into four discrete steps. Since many radical reactions are chain reactions (repeating reactions), we normally write them stepwise:
Step 1: initiation (thermolysis)

Step 2: initiation (abstraction)

Step 3: propagation (addition)

Step 4: propagation (abstraction)

Step 5: termination (dimerization, etc.)

Steps 3 and 4 of this chain reaction are then repeated since the bromide radical can be recycled to step 3. For a chain reaction to produce the desired product, the propagation step must be more advantageous than the termination step. In a practical sense, the neutral reagents are in high concentrations and the radical intermediates are in low concentrations, so the chance of a termination step is quite rare until most of the starting materials have been consumed. Eventually, two radicals will combine to form a \(σ\) bond, ending the chain reaction, but this is so insignificant an event as to be considered inconsequential.
Sometimes, you may suspect that a reaction operates via a radical mechanism. A quick way of determining if radical are produced is to intercept these intermediates with a radical inhibitor. These reagents will act as artificial terminators, and no product will be formed. Common inhibitors are TEMPO, BHA, and BHT. Can you explain why these reagents terminate radical reactions?

While there is a radical HBr addition reaction, there is no corresponding radical addition using HCl or HI. This is peculiar, since we can write identical chain mechanisms! This can be explained by examining the thermodynamics of the two propagation steps.
In the first propagation step, a halide radical adds to a double bond. In order to determine whether this step is favorable, we would need to look at the bond strengths. The overall exothermicity or endothermicity of this step is a combination of the (\(π\)C-C bond strength and the \(σ\)C-X bonds strength). A \(π\)C-C bond has a bond strength of 66 kcal/mol, no matter which hydrogen halide is used. But, the corresponding \(σ\)C-X bond strength depends on the halide.

For the radical HI addition, the first propagation step is substantially endothermic (+9 kcal/mol). Thus, the reaction fails. In the case of HBr and HCl, these are both exothermic for the first propagation step. But, let’s take a look at the second propagation step. This step involves the abstraction of a hydrogen atom from H-X. The overall exothermicity or endothermicity of this step is a combination of the \(σ\)H-X bond strength and the \(σ\)C-H bonds strength. A \(σ\)C-H bond has a bond strength of 98 kcal/mol, no matter which hydrogen halide is used. But, the corresponding \(σ\)H-X bond strength depends on the halide.

For the radical HCl addition, the second propagation step is substantially endothermic (+5 kcal/mol). Thus, the reaction fails.
Free radical halogenation
Besides electrophilic additions and radical additions, another way to make alkyl halides is from alkanes themselves, even though alkanes are notoriously unreactive. Free radical halogenation is the conversion of alkanes into alkyl halides in the presence of Cl2 or Br2 and a source of light.

Before we discuss the mechanism of this reaction, let’s first take a look at some BDE values. These values will be important when we look at the mechanism.

The trends for \(σ\)C-H bond strengths should make sense when we consider radical stabilities (\(σ\)-donation stabilizes radicals).
Free radical halogenation is also a chain reaction. The mechanism for the reaction of methane with Cl2 in the presence of light has the following steps:
Step 1: initiation (photochemical/homolytic cleavage of Cl2)

Step 2: propagation (abstraction of a hydrogen atom to generate the first carbon-centered radical)

Step 3: propagation (addition of carbon-centered radical to generate new \(σ\)C-Cl and chloride radical, which recycles to step 2)

Step 4: termination (dimerization, etc.)

You can see that if we add up the bond enthalpies of all the bonds that are either formed or broken, free radical chlorination is exothermic (~+24 kcal/mol), despite the first propagation step being slightly endothermic. Free radical bromination operates by the same mechanism but is much less exothermic since the first propagation step is highly endothermic (-17 kcal/mol). This will have consequences for selectivity when using more complicated alkanes.
So, what happens when methane is not the starting substrate? Well, since there are many types of hydrogen atoms to abstract in the first propagation step, mixtures of products will result (hence, why this process may not be synthetically useful). For example, the free radical chlorination of butane gives two isomeric chlorides that arise from different hydrogen atoms being abstracted in the first propagation step. What would the ratio of these two products look like? This depends on the number of hydrogen atoms at each site.

For the primary carbon, there are six hydrogen atoms, but for the secondary carbon there are four. So, we might expect that, statistically speaking, the ratio should be 60:40 in favor of 1-chlorobutane, right? Well, the experimental ratio is actually 28:72 in favor of 2-chlorobutane. Why? Because the 2° radical is more stable! Its hydrogen atom is abstracted faster – the energy barrier to get to a 2° radical is much lower. The rate of abstraction of a hydrogen atom at a 2° center is 3.9x faster than at a 1° center. Similarly, a 3° radical is even more stable than a 2° radical, and will form a radical 5.2x faster than at a 1° center.
Thus, the selectivities for chlorination and bromination are as follows:
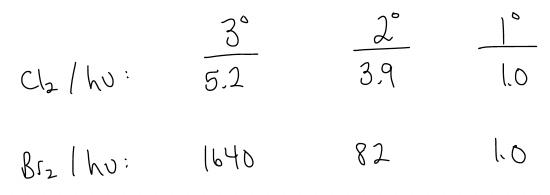
These values tell us that bromination is much more selective. Usually, only the 3° position is halogenated. Why? Let’s look again at the BDE values.
The propagation step for bromination is endothermic, meaning it is more sensitive to the stability of the free radical intermediate. Another way of thinking about this is that the transition state is much more product-like, according to the Hammond postulate, and resemble the radical intermediate more (so any way to stabilize this will be better).
Thus, chlorination of alkanes is used primarily when all hydrogen atoms are equivalent and bromination of alkanes is used to prepare 3° alkyl bromides. Neither fluorine (explosively exothermic) nor iodine (too endothermic to have any appreciable rate) undergo free radical halogenation.

Allylic halogenation
While free radical bromination of tertiary alkanes is highly selective, an even better candidate for free radical halogenation is an allyl system. In cyclohexene, there are three types of \(σ\)C-H bonds where hydrogen atoms could be extracted: vinyl, allylic, and alkyl (methylene). Since abstraction of the allylic hydrogen would lead to the formation of a resonance stabilized allylic radical, the \(σ\)C-H bond is weaker and the BDE much lower. Thus, we can use even milder conditions for this reaction (NBS, CCl4).

Rearrangement of Radicals
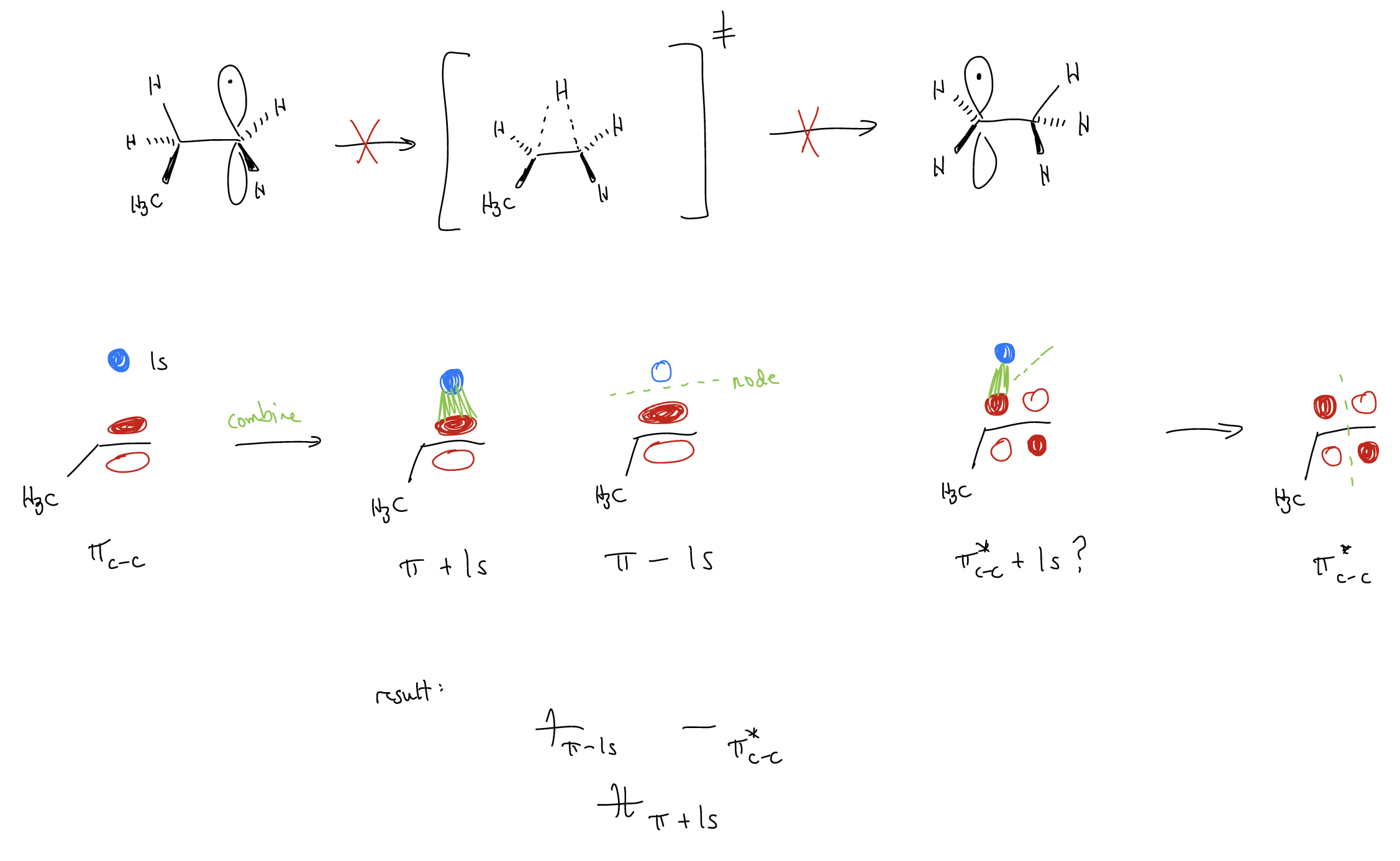
We’ve said that radical intermediates behave similarly to carbocations – they are electron deficient intermediates. Thus, we might think that once we form a radical, it might rearrange to generate an even more stable radical. In the case of carbocation rearrangements, this normally occurred through 1,2-hydride or 1,2-methyl shifts (which are quite fast). By contrast, the 1,2-shifts of hydrogen atoms or alkyl groups are unknown. In order to understand why, we need to look at the molecular orbital description.

Let’s consider the transition state for the rearrangement, in which the hydrogen atom straddles two different carbon atoms. For this, we would need to construct the molecular orbitals for the interaction between a hydrogen 1s orbital, a \(π\)C-C, and a \(π^{*}\)C-C orbital. This would yield three new molecular orbitals. The 1s orbital interacts with \(π\)C-C to give two new molecular orbitals, but there is no interaction with \(π^{*}\)C-C. Why? Because there is no interaction between these orbitals in this geometry. Thus, the third molecular orbital is simply \(π^{*}\)C-C. The energies of these new molecular orbitals can be determined by counting the nodes. The first molecular orbital has no new nodes, but the next two molecular orbitals have one new node each, and will thus be identical in energy. If we then fill the new molecular orbitals with electrons, we see that there will be an electron occupying an antibonding orbital, and this evidently unstable enough to shut down the migration entirely.