Chapter 17.3: The Formation of Complex Ions
- Page ID
- 42138
][\mathrm{NH_3}]^4}=\dfrac{0.0846-x}{x(0.66+4x)^4}\approx\dfrac{0.0846}{x(0.66)^4}=2.1\times10^{13}
\\x&=2.1\times10^{-14}\end{align}\]
The value of x indicates that our assumption was justified. The equilibrium concentration of Cu2+(aq) in a 1.00 M ammonia solution is therefore 2.1 × 10−14 M.
Exercise
The ferrocyanide ion {[Fe(CN)6]4−} is very stable, with a Kf of 1 × 1035. Calculate the concentration of cyanide ion in equilibrium with a 0.65 M solution of K4[Fe(CN)6].
Answer: 2 × 10−6 M
The Effect of the Formation of Complex Ions on Solubility
What happens to the solubility of a sparingly soluble salt if a ligand that forms a stable complex ion is added to the solution? One such example occurs in conventional black-and-white photography, which was discussed briefly in Chapter 4 "Reactions in Aqueous Solution".
Recall that black-and-white photographic film contains light-sensitive microcrystals of AgBr, or mixtures of AgBr and other silver halides. AgBr is a sparingly soluble salt, with a Ksp of 5.35 × 10−13 at 25°C. When the shutter of the camera opens, the light from the object being photographed strikes some of the crystals on the film and initiates a photochemical reaction that converts AgBr to black Ag metal. Well-formed, stable negative images appear in tones of gray, corresponding to the number of grains of AgBr converted, with the areas exposed to the most light being darkest. To fix the image and prevent more AgBr crystals from being converted to Ag metal during processing of the film, the unreacted AgBr on the film is removed using a complexation reaction to dissolve the sparingly soluble salt.
The reaction for the dissolution of silver bromide is as follows:
\[AgBr_{(s)} \rightleftharpoons Ag^+_{(aq)} + Br^{−}_{(aq)} \tag{17.3.4a}\]
with
\[K_{sp} = 5.35 \times 10^{−13} \text{ at 25°C} \tag{17.3.4b}\]
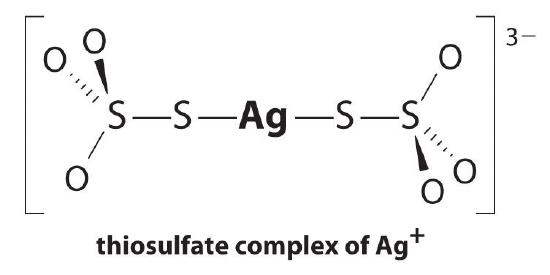
The equilibrium lies far to the left, and the equilibrium concentrations of Ag+ and Br− ions are very low (7.31 × 10−7 M). As a result, removing unreacted AgBr from even a single roll of film using pure water would require tens of thousands of liters of water and a great deal of time. Le Châtelier’s principle tells us, however, that we can drive the reaction to the right by removing one of the products, which will cause more AgBr to dissolve. Bromide ion is difficult to remove chemically, but silver ion forms a variety of stable two-coordinate complexes with neutral ligands, such as ammonia, or with anionic ligands, such as cyanide or thiosulfate (S2O32−). In photographic processing, excess AgBr is dissolved using a concentrated solution of sodium thiosulfate.
The reaction of Ag+ with thiosulfate is as follows:
\[Ag^+_{(aq)} + 2S_2O^{2−}_{3(aq)} \rightleftharpoons [Ag(S_2O_3)_2]^{3−}_{(aq)} \tag{17.3.5a}\]
with
\[K_f = 2.9 \times 10^{13} \tag{17.10b}\]
The magnitude of the equilibrium constant indicates that almost all Ag+ ions in solution will be immediately complexed by thiosulfate to form [Ag(S2O3)2]3−. We can see the effect of thiosulfate on the solubility of AgBr by writing the appropriate reactions and adding them together:
\\ \mathrm{Ag^+(aq)}+\mathrm{2S_2O_3^{2-}(aq)}\rightleftharpoons\mathrm{[Ag(S_2O_3)_2]^{3-}(aq)}\hspace{3mm}K_\textrm f&=2.9\times10^{13}
\\ \mathrm{AgBr(s)}+\mathrm{2S_2O_3^{2-}(aq)}\rightleftharpoons\mathrm{[Ag(S_2O_3)_2]^{3-}(aq)}+\mathrm{Br^-(aq)}\hspace{3mm}K&=K_{\textrm{sp}}K_{\textrm f}=15\end{align} \tag{17.3.6}\)
Comparing K with Ksp shows that the formation of the complex ion increases the solubility of AgBr by approximately 3 × 1013. The dramatic increase in solubility combined with the low cost and the low toxicity explains why sodium thiosulfate is almost universally used for developing black-and-white film. If desired, the silver can be recovered from the thiosulfate solution using any of several methods and recycled.
Note the Pattern
If a complex ion has a large Kf, the formation of a complex ion can dramatically increase the solubility of sparingly soluble salts.
Example 17.3.2
Due to the common ion effect, we might expect a salt such as AgCl to be much less soluble in a concentrated solution of KCl than in water. Such an assumption would be incorrect, however, because it ignores the fact that silver ion tends to form a two-coordinate complex with chloride ions (AgCl2−). Calculate the solubility of AgCl in each situation:
- in pure water
- in 1.0 M KCl solution, ignoring the formation of any complex ions
- the same solution as in part (b) except taking the formation of complex ions into account, assuming that AgCl2− is the only Ag+ complex that forms in significant concentrations
At 25°C, Ksp = 1.77 × 10−10 for AgCl and Kf = 1.1 × 105 for AgCl2−.
Given: Ksp of AgCl, Kf of AgCl2−, and KCl concentration
Asked for: solubility of AgCl in water and in KCl solution with and without the formation of complex ions
Strategy:
A Write the solubility product expression for AgCl and calculate the concentration of Ag+ and Cl− in water.
B Calculate the concentration of Ag+ in the KCl solution.
C Write balanced chemical equations for the dissolution of AgCl and for the formation of the AgCl2− complex. Add the two equations and calculate the equilibrium constant for the overall equilibrium.
D Write the equilibrium constant expression for the overall reaction. Solve for the concentration of the complex ion.
Solution:
-
A If we let x equal the solubility of AgCl, then at equilibrium [Ag+] = [Cl−] = x M. Substituting this value into the solubility product expression,
Ksp = [Ag+][Cl−] = (x)(x) = x2 =1.77×10−10x = 1.33×10−5Thus the solubility of AgCl in pure water at 25°C is 1.33 × 10−5 M.
-
B If x equals the solubility of AgCl in the KCl solution, then at equilibrium [Ag+] = x M and [Cl−] = (1.0 + x) M. Substituting these values into the solubility product expression and assuming that x << 1.0,
Ksp = [Ag+][Cl−] = (x)(1.0 + x) ≈ x(1.0) = 1.77×10−10 = xIf the common ion effect were the only important factor, we would predict that AgCl is approximately five orders of magnitude less soluble in a 1.0 M KCl solution than in water.
-
C To account for the effects of the formation of complex ions, we must first write the equilibrium equations for both the dissolution and the formation of complex ions. Adding the equations corresponding to Ksp and Kf gives us an equation that describes the dissolution of AgCl in a KCl solution. The equilibrium constant for the reaction is therefore the product of Ksp and Kf:
\(\begin{align}\mathrm{AgCl(s)}\rightleftharpoons\mathrm{Ag^+(aq)}+\mathrm{Cl^-(aq)}\hspace{3mm}K_{\textrm{sp}}&=1.77\times10^{-10}
\\ \mathrm{Ag^+(aq)}+\mathrm{2Cl^{-}}\rightleftharpoons\mathrm{[AgCl_2]^{-}}\hspace{3mm}K_\textrm f&=1.1\times10^{5}
\\ \mathrm{AgCl(s)}+\mathrm{Cl^{-}}\rightleftharpoons\mathrm{[AgCl_2]^{-}}\hspace{3mm}K&=K_{\textrm{sp}}K_{\textrm f}=1.9\times10^{-5}\end{align}\)D If we let x equal the solubility of AgCl in the KCl solution, then at equilibrium [AgCl2−] = x and [Cl−] = 1.0 − x. Substituting these quantities into the equilibrium constant expression for the net reaction and assuming that x << 1.0,
\(K=\dfrac{[\mathrm{AgCl_2^-}]}{[\mathrm{Cl^-}]}=\dfrac{x}{1.0-x}\approx1.9\times10^{-5}=x\)That is, AgCl dissolves in 1.0 M KCl to produce a 1.9 × 10−5 M solution of the AgCl2− complex ion. Thus we predict that AgCl has approximately the same solubility in a 1.0 M KCl solution as it does in pure water, which is 105 times greater than that predicted based on the common ion effect. (In fact, the measured solubility of AgCl in 1.0 M KCl is almost a factor of 10 greater than that in pure water, largely due to the formation of other chloride-containing complexes.)
Exercise
Calculate the solubility of mercury(II) iodide (HgI2) in each situation:
- pure water
- a 3.0 M solution of NaI, assuming [HgI4]2− is the only Hg-containing species present in significant amounts
Ksp = 2.9 × 10−29 for HgI2 and Kf = 6.8 × 1029 for [HgI4]2−.
Answer:
- 1.9 × 10−10 M
- 1.4 M
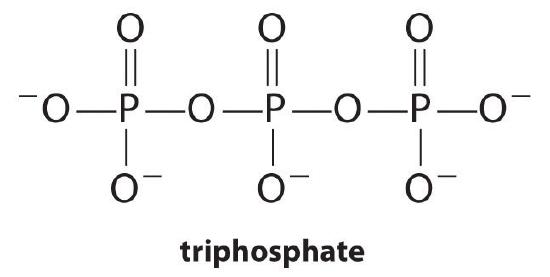
Complexing agents, molecules or ions that increase the solubility of metal salts by forming soluble metal complexes, are common components of laundry detergents. Long-chain carboxylic acids, the major components of soaps, form insoluble salts with Ca2+ and Mg2+, which are present in high concentrations in “hard” water. The precipitation of these salts produces a bathtub ring and gives a gray tinge to clothing. Adding a complexing agent such as pyrophosphate (O3POPO34−, or P2O74−) or triphosphate (P3O105−) to detergents prevents the magnesium and calcium salts from precipitating because the equilibrium constant for complex-ion formation is large:
However, phosphates can cause environmental damage by promoting eutrophication, the growth of excessive amounts of algae in a body of water, which can eventually lead to large decreases in levels of dissolved oxygen that kill fish and other aquatic organisms. Consequently, many states in the United States have banned the use of phosphate-containing detergents, and France has banned their use beginning in 2007. “Phosphate-free” detergents contain different kinds of complexing agents, such as derivatives of acetic acid or other carboxylic acids. The development of phosphate substitutes is an area of intense research.
Commercial water softeners also use a complexing agent to treat hard water by passing the water over ion-exchange resins, which are complex sodium salts. When water flows over the resin, sodium ion is dissolved, and insoluble salts precipitate onto the resin surface. Water treated in this way has a saltier taste due to the presence of Na+, but it contains fewer dissolved minerals.
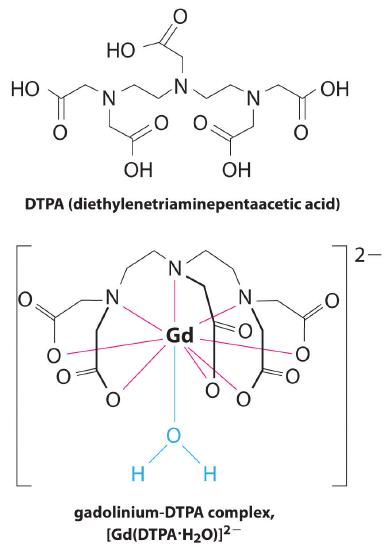
Another application of complexing agents is found in medicine. Unlike x-rays, magnetic resonance imaging (MRI) can give relatively good images of soft tissues such as internal organs. MRI is based on the magnetic properties of the 1H nucleus of hydrogen atoms in water, which is a major component of soft tissues. Because the properties of water do not depend very much on whether it is inside a cell or in the blood, it is hard to get detailed images of these tissues that have good contrast. To solve this problem, scientists have developed a class of metal complexes known as “MRI contrast agents.” Injecting an MRI contrast agent into a patient selectively affects the magnetic properties of water in cells of normal tissues, in tumors, or in blood vessels and allows doctors to “see” each of these separately (Figure 17.3.2). One of the most important metal ions for this application is Gd3+, which with seven unpaired electrons is highly paramagnetic. Because Gd3+(aq) is quite toxic, it must be administered as a very stable complex that does not dissociate in the body and can be excreted intact by the kidneys. The complexing agents used for gadolinium are ligands such as DTPA5− (diethylene triamine pentaacetic acid), whose fully protonated form is shown here.
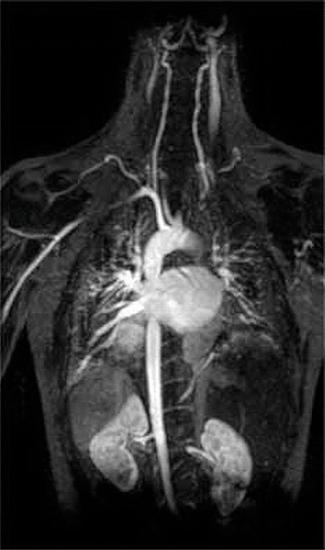
Figure 17.3.2 An MRI Image of the Heart, Arteries, and Veins When a patient is injected with a paramagnetic metal cation in the form of a stable complex known as an MRI contrast agent, the magnetic properties of water in cells are altered. Because the different environments in different types of cells respond differently, a physician can obtain detailed images of soft tissues.
Summary
A complex ion is a species formed between a central metal ion and one or more surrounding ligands, molecules or ions that contain at least one lone pair of electrons. Small, highly charged metal ions have the greatest tendency to act as Lewis acids and form complex ions. The equilibrium constant for the formation of the complex ion is the formation constant (Kf). The formation of a complex ion by adding a complexing agent increases the solubility of a compound.
Key Takeaway
- The formation of complex ions can substantially increase the solubility of sparingly soluble salts if the complex ion has a large Kf.
Conceptual Problems
-
What is the difference between Keq and Kf?
-
Which would you expect to have the greater tendency to form a complex ion: Mg2+ or Ba2+? Why?
-
How can a ligand be used to affect the concentration of hydrated metal ions in solution? How is Ksp affected? Explain your answer.
-
Co(II) forms a complex ion with pyridine (C5H5N). Which is the Lewis acid, and which is the Lewis base? Use Lewis electron structures to justify your answer.
Numerical Problems
-
Fe(II) forms the complex ion [Fe(OH)4]2− through equilibrium reactions in which hydroxide replaces water in a stepwise manner. If log K1 = 5.56, log K2 = 4.21, log K3 = −0.10, and log K4 = −1.09, what is Kf? Write the equilibrium equation that corresponds to each stepwise equilibrium constant. Do you expect the [Fe(OH)4]2− complex to be stable? Explain your reasoning.
-
Zn(II) forms the complex ion [Zn(NH3)4]2+ through equilibrium reactions in which ammonia replaces coordinated water molecules in a stepwise manner. If log K1 = 2.37, log K2 = 2.44, log K3 = 2.50, and log K4 = 2.15, what is the overall Kf? Write the equilibrium equation that corresponds to each stepwise equilibrium constant. Do you expect the [Zn(NH3)4]2+ complex to be stable? Explain your reasoning.
-
Although thallium has limited commercial applications because it is toxic to humans (10 mg/kg body weight is fatal to children), it is used as a substitute for mercury in industrial switches. The complex ion [TlBr6]3− is highly stable, with log Kf = 31.6. What is the concentration of Tl(III)(aq) in equilibrium with a 1.12 M solution of Na3[TlBr6]?
Answer
- [Fe(H2O)6]2+(aq) + OH−(aq) ⇌ [Fe(H2O(aq))5(OH)] + (aq) + H2O log K1 = 5.56[Fe(H2O)5(OH)] + (aq) + OH−(aq) ⇌ [Fe(H2O)4(OH)2](aq) + H2O(aq) log K2 = 9.77[Fe(H2O)4(OH)2](aq) + OH−(aq) ⇌ [Fe(H2O)3(OH)3]−(aq) + H2O(aq) log K3 = 9.67[Fe(H2O)3(OH)3]−(aq) + OH−(aq) ⇌ [Fe(OH)4]2−(aq) + 3H2O(l) log K4 = 8.58[Fe(H2O)6]2+(aq) + 4OH−(aq) ⇌ [Fe(OH)4]2−(aq) + 6H2O(l)log Kf = log K1 + log K2 + log K2 + log K4= 33.58
Thus, Kf = 3.8 × 1033. Because [Fe(OH)4]2− has a very large value of Kf, it should be stable in the presence of excess OH−.
Contributors
- Anonymous
Modified by Joshua B. Halpern